Lecture 5. DISCRETE PROBABILITYLecture 5. DISCRETE PROBABILITY
Random Variable
Probability Distribution
Expected value
Variance – Standard Deviation
Bivariate Probability
Binomial Distribution
[1] Chapter 5: pp.215 - 260
PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 1
5.1. Random Variable5.1. Random Variable
Random variable: numerical value from a random
experiment.
Denoted by X, Y, Z, or X1, X2,...
Ex. Tossing a die, Xis the number of dots
- Number of boys in a 3-children family
- Score of students’ exam
- Temparature during a day
- Interest rates in a period of time
PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 2
Types of Random VariableTypes of Random Variable
Variable , value is random
Discrete variable: = (, , … , )
Number of item: = (0, 1, 2, … )
Score of test: = (0, 1, 2, … , 100)
( = )is a random event
Continuous variable: = (; )
Time
Temperature
Length, Weight
PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 3
5.2. Discrete Probability Distribution5.2. Discrete Probability Distribution
Discrete: = (, , … , )
Denote: = =
Property:
∑
 = 1
is discrete probabitily distribution; probabitiy
function
PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 4
Value …
Probability …
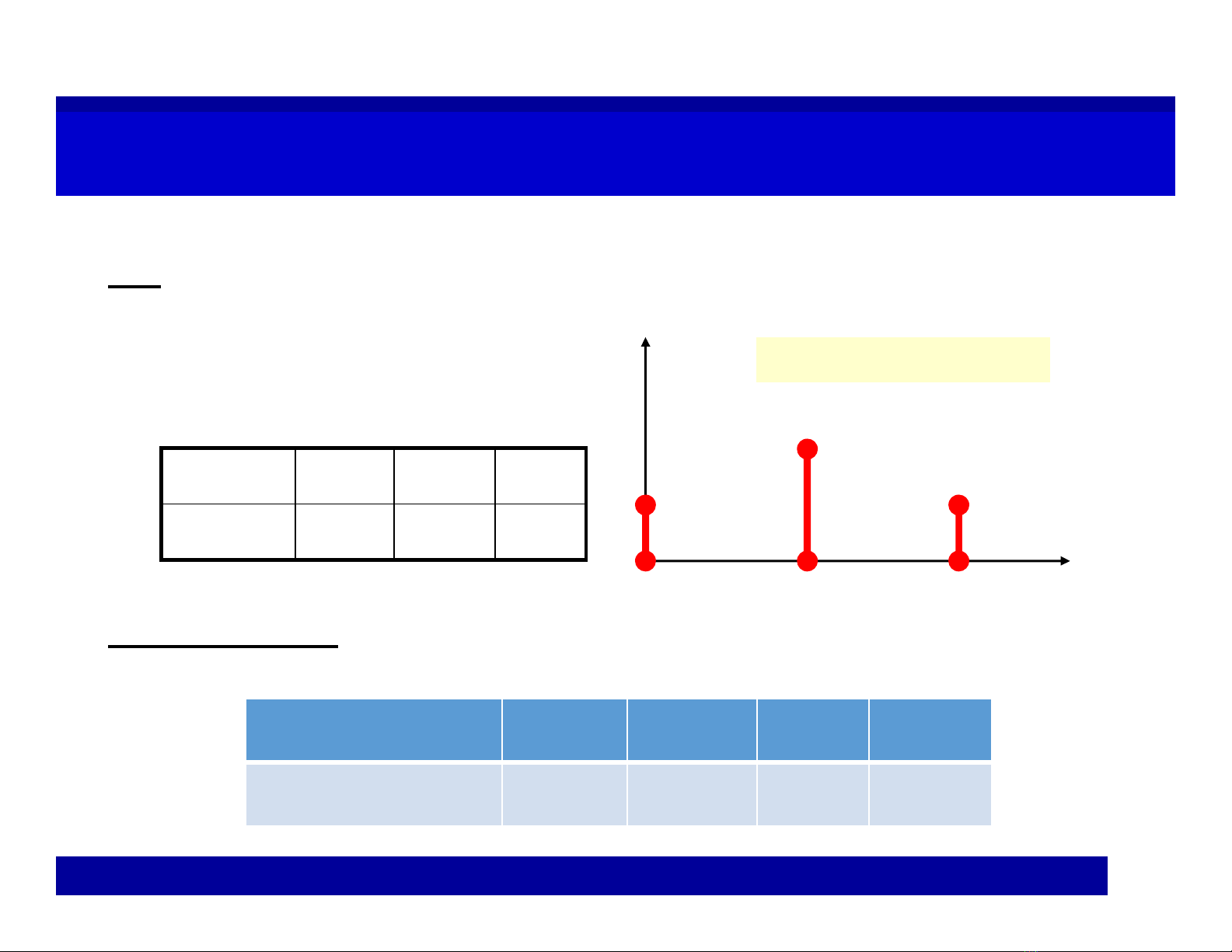
ExampleExample
Ex. Probability distribution of X, which is the number of
Heads when flipping a coin twice
X = {0, 1, 2}
Example 5.1. Number of Head when flipping a coin 3
times
PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 5
x0 1 2
P(x) 1/4 2/4 1/4
Flip a coin twice
p
X 0 1 2 3
Probability