Lecture 6. CONTINUOUS PROBABILITYLecture 6. CONTINUOUS PROBABILITY
Continuous Random Variable
Density Function
Parameter
Uniform Distribution
Normal Distribution
Cutoff point
[1] Chapter 6. pp. 255 - 294
PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 1
6.1. Continuous Random Variable6.1. Continuous Random Variable
Continuous Random Variable: uncountable values
Available value is one interval: =(,)
Maybe:  =−∞; =+∞
Probability that one point: ==0
Consider Probability at one interval: ( < <)
PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 2
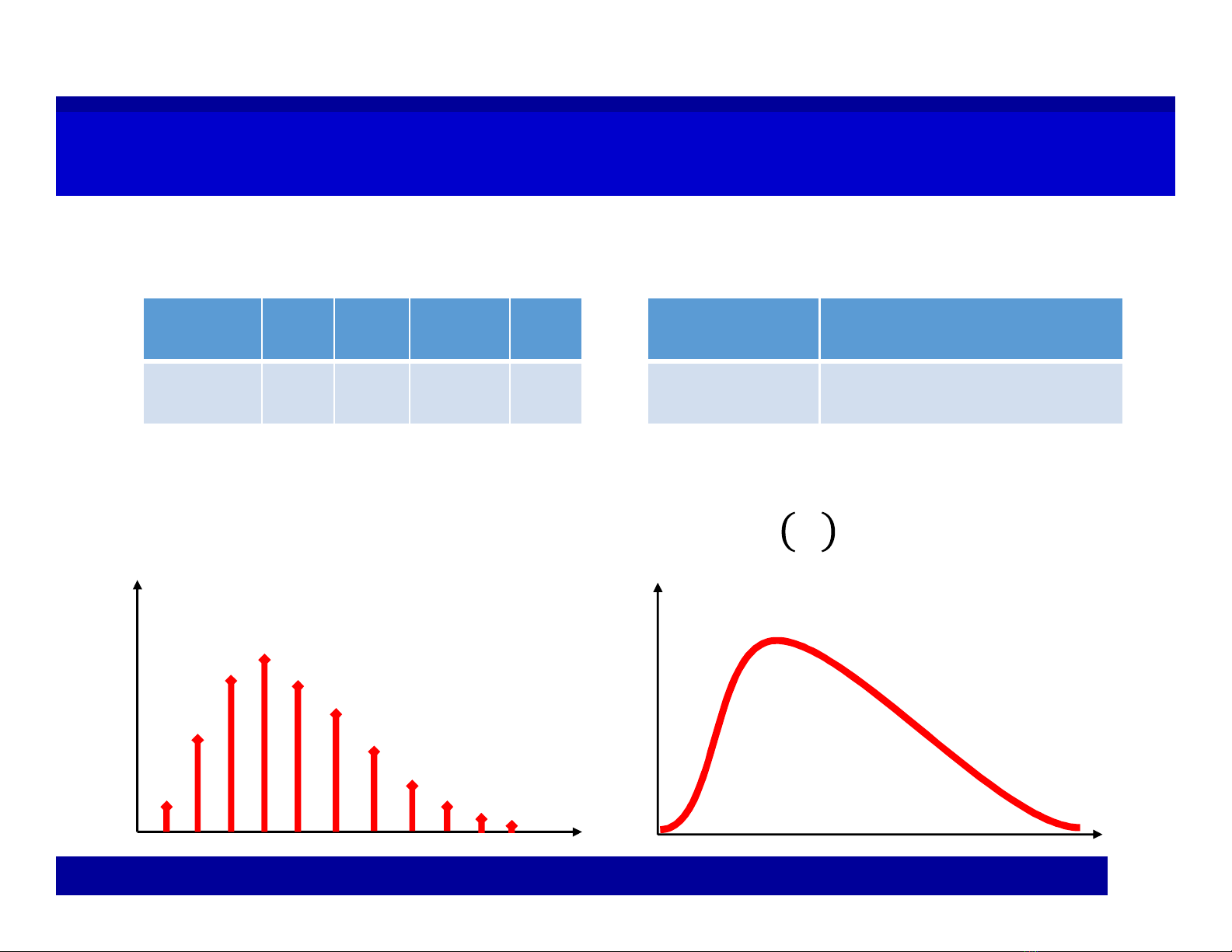
6.2. Density Function6.2. Density Function
Discrete Continuous
∑
=1
∫


 =1
PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 3
X…
Prob. …
X(,)
Density ()
f(x)
p
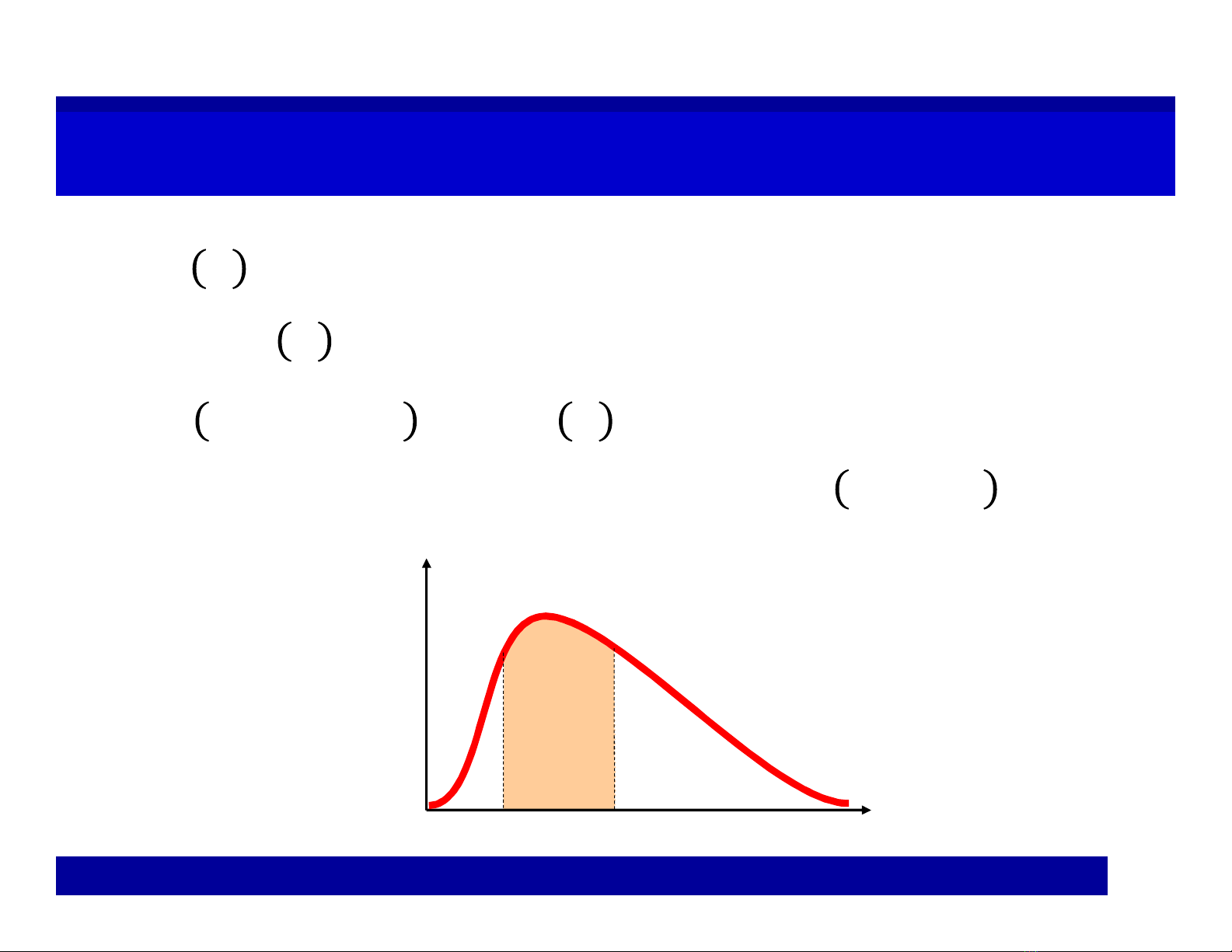
Density FunctionDensity Function
≥0
∫


 =1
<< =
∫

Cutoff point level denoted by : >=
PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 4
f(x)
a b
6.3. Parameter6.3. Parameter
Expected Value:
==
∫
 


Variance: =
∫
− 


=
∫


 −
Standard Deviation= ()
Cutoff point level , denoted by :
>
=
PROBABILITY & STATISTICS – Bui Duong Hai – NEU – www.mfe.edu.vn/buiduonghai 5