CHUYÊN Đ H PH NG TRÌNH ĐI SỀ Ệ ƯƠ Ạ Ố
A/ Ki n th c c b nế ứ ơ ả
1. Ph ng pháp th ươ ế
B c 1: T m t ph ng trình c a h đã cho (coi là PT (1)), ta bi u di n m t n theo nướ ừ ộ ươ ủ ệ ể ễ ộ ẩ ẩ
kia, r i th ồ ế vào ph ng trình th hai (PT (2)) đ đc m t ph ng trình m i (ch còn m tươ ứ ể ượ ộ ươ ớ ỉ ộ
n).ẩ
B c 2: Dùng ph ng trình m i y đ thay th cho PT (2) trong h (PT (1) cũng th ng ướ ươ ớ ấ ể ế ệ ườ
đc thay th b i h th c bi u di n m t n theo n kia).ượ ế ở ệ ứ ể ễ ộ ẩ ẩ
2. Ph ng pháp c ng đi sươ ộ ạ ố
B c 1: C ng hay tr t ng v hai ph ng trình c a h ph ng trình đã cho đ đcướ ộ ừ ừ ế ươ ủ ệ ươ ể ượ
m t ộph ng trình m i.ươ ớ
B c 2: Dùng ph ng trình m i y thay th cho m t trong hai ph ng trình c a h (gi ướ ươ ớ ấ ế ộ ươ ủ ệ ữ
nguyên ph ng trình kia).ươ
Chú ý:
Trong ph ng pháp c ng đi s , tr c khi th c hi n b c 1, có th nhân hai v c a m iươ ộ ạ ố ướ ự ệ ướ ể ế ủ ỗ
ph ng trình v i m t s thích h p (n u c n) sao cho các h s c a m t n nào đó trongươ ớ ộ ố ợ ế ầ ệ ố ủ ộ ẩ
hai ph ng trình c a h là b ng nhau ho c đi nhau.ươ ủ ệ ằ ặ ố
Đôi khi ta có th dùng ph ng pháp đt n ph đ đa h ph ng trình đã cho v hể ươ ặ ẩ ụ ể ư ệ ươ ề ệ
ph ng ươ trình v i hai n m i, r i sau đó s d ng m t trong hai ph ng pháp gi i trên.ớ ẩ ớ ồ ử ụ ộ ươ ả ở
B/ Các d ng bài t pạ ậ
D ng 1: H ph ng trình b c nh t hai n đã ạ ệ ươ ậ ấ ẩ d ng c b nở ạ ơ ả
' ' '
ax by c
a x b y c
+ =
+ =
Ph ng pháp gi i: Áươ ả p d ng ph ng pháp c ng và th đ đa v ụ ươ ộ ế ể ư ề pt b c nh t m t nậ ấ ộ ẩ để
gi iả
Bài t p:ậ Gi i các ph ng trình sau:ả ươ
D¹ng 1 a)
2 3 2
3 2 3
x y
x y
￬ + = -
￬
￬
￬
￬
￬- = -
￬
￬
￬
b)
4 3 6
2 0
x y
x y
￬ + =
￬
￬
￬
￬
￬+ =
￬
￬
￬
D¹ng 2 a)
2 0
3 4
5 11
x y
x y
￬
￬+ - =
￬
￬￬
￬
￬- =
￬
￬
￬
￬
b)
1
5 3 3
4 5 10 0
a b
a b
￬
￬
￬+ = -
￬
￬
￬
￬
￬- - =
￬
￬
￬
D¹ng 3: a)
6( ) 8 2 3
5( ) 5 3 2
x y x y
y x x y
￬+ = + -
￬
￬
￬
￬
￬- = + +
￬
￬
￬
b)
( 1)( 2) ( 1)( 3)
( 5)( 4) ( 4)( 1)
x y x y
x y x y
￬- - = + -
￬
￬
￬
￬
￬- + = - +
￬
￬
￬
D¹ng 4: a)
2 3 1
3 2
x y
x y
￬
￬- =
￬
￬
￬
￬+ =
￬
￬
￬
b)
D ng 2: H ph ng trình có m t ph ng trình b c nh t và m t ph ng trình b c ạ ệ ươ ộ ươ ậ ấ ộ ươ ậ
hai.
a/ Ph ng pháp gi i:ươ ả Rút m t n t ph ng trình b c nh t th vào ph ng trình b c ộ ẩ ừ ươ ậ ấ ế ươ ậ
hai ta đa đc v d ng h ph ng trình g m m t ph ng trình b c nh t và m t ư ượ ề ạ ệ ươ ồ ộ ươ ậ ấ ộ
ph ng trình b c hai m t n => gi i ph ng trình b c hai m t n.ươ ậ ộ ẩ ả ươ ậ ộ ẩ
b/ Ví d :ụ gi i h ph ng trình sau: ả ệ ươ
( ) ( )
2 2
2
2 2 2
4 2 4 2
2 4 4 2 2
8 16 8 0 1
4 8 4 2 4 8 0 8 1 0
x y x y
x y x y x
y y y
x y y y y
= − = −
+ = = − =
− + = =
+ = − + − = − =
c/ Bài t p áp d ng:ậ ụ Gi i các h ph ng trình sau:ả ệ ươ
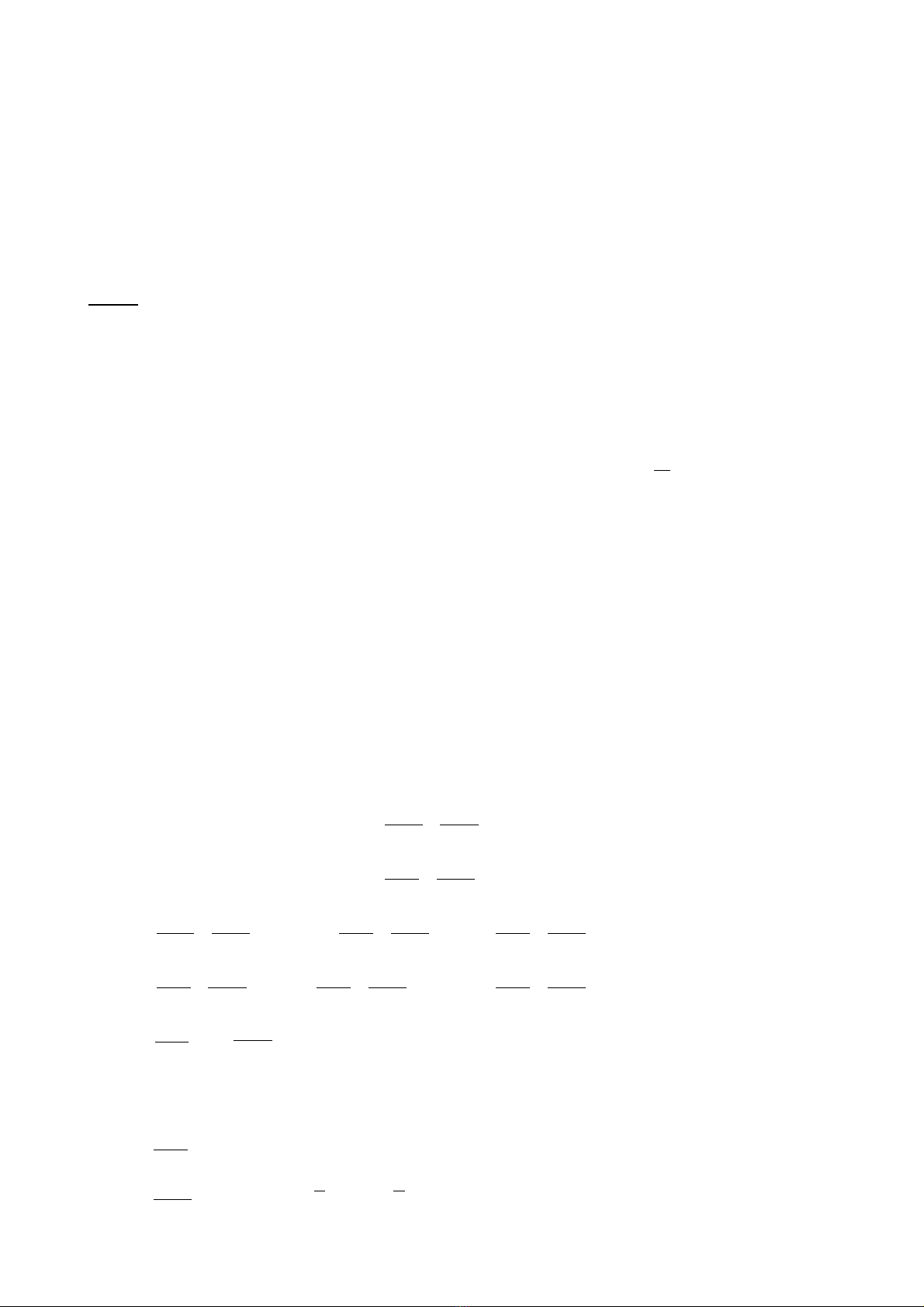
a)
2 2
1 0
2 3 7 12 1 0
x y
x xy y x y
￬- + =
￬
￬
￬
￬
￬- + - - + =
￬
￬
￬
b)
2 2
5 1
3 10
x y
x y xy x y
￬ - = -
￬
￬
￬
￬
￬+ - + + =
￬
￬
￬
c)
2 2
2 2 23 0
3 3 0
x y x y
x y
￬
￬ + - - - =
￬
￬
￬
￬- - =
￬
￬
￬
d)
2
3 6 3 0
4 9 6
x xy x y
x y
￬
￬ + - + =
￬
￬
￬
￬- =
￬
￬
￬
D ng 3: H ph ng trình có m t ph ng trình đa đc v d ng ph ng trình tích.ạ ệ ươ ộ ươ ư ượ ề ạ ươ
a/ Cách gi i:ả
( , ). ( , ) 0 ( , ) 0 ( , ) 0
C( , ) 0 C( , ) 0 C( , ) 0
A x y B x y A x y B x y
hoac
x y x y x y
= = =
= = =
r i gi i hai tr ng h p.ồ ả ườ ợ
Chú ý: Thông th ng d ng này g m m t ph ng trình b c nh t hai n và m t ph ng trình b cườ ạ ồ ộ ươ ậ ấ ẩ ộ ươ ậ
hai nên ta có th gi i theo cách làm d ng 1:ể ả ở ạ
b/ Ví d :ụ Gi i h ph ng trình sau: ả ệ ươ
( ) ( )
1 0 1 0
1 1 0
3 2 22 3 2 22
3 2 22
x y xy x
x y
x y x y
x y
￬
￬ ￬
￬
￬ ￬
+ + + = + =
+ + =
￬
￬ ￬
￬ ￬ ￬
￬ ￬
￬ ￬ ￬
￬ ￬ ￬
- = - =
- =
￬ ￬ ￬
￬ ￬
￬ ￬
￬
￬
ho c ặ
1 0
3 2 22
y
x y
￬
￬+ =
￬
￬
￬
￬- =
￬
￬
￬
1/
1 0 1
3 2 22 12, 5
x x
x y y
￬ ￬
￬ ￬
+ = = -
￬ ￬
￬ ￬
￬
￬ ￬
￬ ￬
- = = -
￬ ￬
￬ ￬
￬ ￬
2/
1
1 0
20
3 2 22
3
y
y
x y x
￬
￬= -
￬￬
￬+ = ￬
￬
￬ ￬
￬
￬ ￬
￬ ￬
- = =
￬ ￬
￬
￬￬
￬
￬
c/ Bài t p áp d ng:ậ ụ Gi i các h ph ng trình sau: ả ệ ươ
a)
2 2
1 0
22
x y xy
x y x y
￬ + + + =
￬
￬
￬
￬
￬+ - - =
￬
￬
￬
b)
2
( 2 1)( 2 2) 0
3 1 0
x y x y
xy y y
￬+ + + + =
￬
￬
￬
￬
￬+ + + =
￬
￬
￬
c)
(2 3 2)( 5 3) 0
3 1
x y x y
x y
￬+ - - - =
￬
￬
￬
￬
￬- =
￬
￬
￬
d)
2 2
( 2)(2 2 1) 0
3 32 5 0
x y x y
x y
￬+ + + - =
￬
￬
￬
￬
￬+ + =
￬
￬
￬
e)
2
( ) 3( ) 2 0
3 5 5 0
x y x y
x y
￬
￬+ - + + =
￬
￬
￬
￬- - =
￬
￬
￬
f)
2 2
( 1) ( 1) 0
2 3 5 0
x y
x y
￬
￬- - + =
￬
￬
￬
￬+ - =
￬
￬
￬
D ng 4:ạ H gi i b ng ph ng pháp đt n phệ ả ằ ươ ặ ẩ ụ:
Chú ý: C n s d ng các phép bi n đi đng nh t đ đa các h ph ng trình đã ầ ử ụ ế ổ ồ ấ ể ư ệ ươ
cho v d ng h ph ng trình đt đc n ph .ề ạ ệ ươ ặ ượ ẩ ụ
a/ Ví d :ụ Gi i h ph ng trình sau: ả ệ ươ
2 2 6
1 2
5 1 3
1 2
x
x y
x y
+
+ =
+ −
− =
+ −
ĐKXĐ: x
- 1, y
2
2 2 1 2 1 2
6 1 6 5
1 2 1 2 1 2
5 1 5 1 5 1
3 3 3
1 2 1 2 1 2
x
x y x y x y
x y x y x y
+
+ = + + = + =
+ − + − + −
− = − = − =
+ − + − + −
Đt u = ặ
1
1x+
, v =
1
2y−
H ph ng trình đã cho tr thànhệ ươ ở :
2 5 1
5 3 2
u v u
u v v
+ = =
− = =
Suy ra
111 1 0
11 5
12
22 2
2
x x
x
y y
y
=+ = =
+


− = =

=
−
(Tho mãn ĐKXĐ)ả
V y h ph ng trình đã cho có nghi m là: (x;y) = (0; ậ ệ ươ ệ
5
2
)
b/ Bài t p áp d ng:ậ ụ Gi i các h ph ng trình sau:ả ệ ươ
1/
5
2
34
1
2
11
yx
yx
2/
2 2 6
1 2
5 1 3
1 2
x
x y
x y
+
+ =
+ −
− =
+ −
3/
( )
( )
12 3
3 2
x y
x
x x y x
+ + =
+ − =
4/
7,1
13
2
52
yxx
yxx
5/
1 2 2
2 1
3 4
x y x y
x y x y
x y
+ + +
+ =
+ + +
+ =
6/
12
223
yx
yx
7/
2
1
1
1
1
1
1
1
1
2
yx
yx
8/
2 6 3 1 5
5 6 4 1 1
x y
x y
− + + =
− − + =
9/
3 1
3
x y
y x
+ − =
− =
10/
3 5 2
2 2
1 1 2
2 2 15
x y x y
x y x y
+ =
− +
− =
− +
11)
3 2 17
x 2 y 1 5
2x 2 y 2 26
x 2 y 1 5
+ =
− −
− +
+ =
− −
12)
( ) ( )
2
3 4
2 3 12
x y x y
x y
− + − =
+ =
D ng ạ5: H đi x ng lo i I ệ ố ứ ạ ( Là h ph ng trình vai trò c a x và y là nh ệ ươ ủ ư
nhau)
( ; ) 0
( ; ) 0
f x y
g x y
=
=
trong đó f(x;y) = f(y;x), g(x;y) = g(y;x).
a/ Cách gi i: ảTính t ng (ho c tích) hai n (ổ ặ ẩ đa v ph ng trình n ph là t ng ho cư ề ươ ẩ ụ ổ ặ
tích hai nẩ), tìm n t tích (ho c) t ng hai n ố ặ ổ ẩ
áp d ng h th c vi ét đa v pt b c 2ụ ệ ứ ư ề ậ
m t n….ộ ẩ
b/ Ví d :ụ Gi i h ph ng trình: ả ệ ươ
( )
( ) ( )
( )
( )
( )
7 2 24 7 2 24
7 7 2 24
5 5 5 5 5 10 2 10
17 34 2
5
5 5
x y xy x y xy
x y xy
x y xy x y xy x y xy
x y x y
xy
x y xy
+ − = + − =
+ − =
+ + = + + = + + =
+ = + =
= −
+ + =
Do đó x; y là hai nghi m c a ph ng trình: ệ ủ ươ
2
2 5 0 1 6X X X− − = =
V y h ph ng trình có nghi m: ậ ệ ươ ệ
( ) ( )
1 6;1 6 ; 1 6;1 6+ − − +
c/ Bài t p áp d ng:ậ ụ Gi i các h ph ng trình sau: ả ệ ươ
1/
12
25
22
xy
yx
2/
2 2
2
3
xy
x y xy
=
+ − =
3/
2 2
7
13
x y xy
x y xy
￬+ + =
￬
￬
￬
￬
￬+ + =
￬
￬
￬
4/
2 2
1
6
x y xy
x y y x
￬ + + = -
￬
￬
￬
￬
￬+ = -
￬
￬
￬
5/
2 2
102
69
x y x y
xy x y
￬
￬ + - - =
￬
￬
￬
￬+ + =
￬
￬
￬
6/
2 2
3( )
160
x y xy
x y
￬+ =
￬
￬
￬
￬
￬+ =
￬
￬
￬
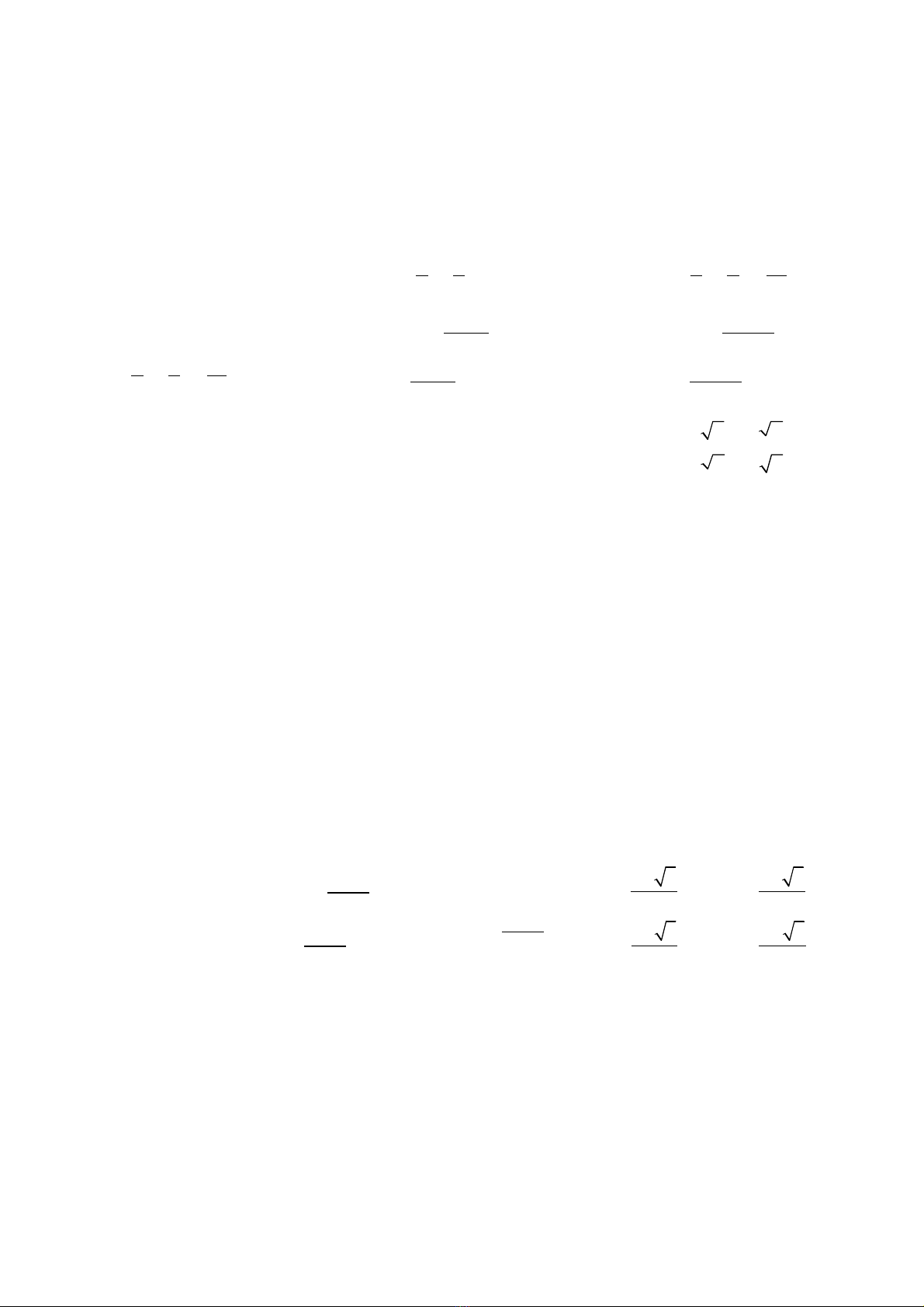
7/
2 2
( 2)( 2) 9
2( ) 6
xy x y
x y x y
￬+ + =
￬
￬
￬
￬
￬+ + + =
￬
￬
￬
8/
2 2
2 ( 3) 2 ( 3) 9 0
2( ) 6 0
x y x y y x
x y xy
￬+ + - + - + =￬
￬
￬
￬
￬+ - + =
￬
￬
￬
9/
2 2
3 3
1x y xy
x y x y
￬+ + =￬
￬
￬
￬
￬+ = +
￬
￬
￬
10/
( 1) ( 1) 17
( 1)( 1) 8
x x y y xy
x y
￬+ + + + =
￬
￬
￬
￬
￬+ + =
￬
￬
￬
11/
2 2
5
7
x y xy
x y xy
+ + =
￬
￬
￬
￬
￬
￬+ + =
￬
￬
￬
12/
11
6 6 11
xy x y
xy
x y
￬ + + =
￬
￬
￬
￬
￬
￬+ + =
￬
￬
￬
￬
13/
7
10
3
xy x y
x y
y x
￬ + + =
￬
￬
￬
￬
￬
￬+ =
￬
￬
￬
￬
14/
2 2
52
1 1 5
12
x y
x y
￬+ =￬
￬
￬
￬
￬
￬+ =
￬
￬
￬
￬
15/
11
2
xx y
x
x y
￬
￬
￬+ = -
￬
￬ +
￬
￬
￬
￬= -
￬
￬+
￬
￬
16/
15
2
6
2
yx y
x
x y
￬
￬
￬+ = -
￬
￬ -
￬
￬
￬
￬=
￬
￬-
￬
￬
17/
3 3
2 2
9
5
x y
x y
￬+ =
￬
￬
￬
￬
￬+ =
￬
￬
￬
18/
3 3
7
133
x y
x y
￬ + =
￬
￬
￬
￬
￬+ =
￬
￬
￬
19/
30
35
x y y x
x x y y
￬+ =
￬
￬
￬
￬
￬+ =
￬
￬
￬
D ng ạ6: H đi x ng lo i Iệ ố ứ ạ I ( Là h ph ng trình vai trò c a x ệ ươ ủ ph ng ở ươ
trình này là y c a ph ng trình kia và ng c l i)ủ ươ ượ ạ
( ; ) 0
( ; ) 0
f x y
g x y
=
=
trong đó f(x;y) = g(y;x).
a/ Cách gi iả: Tr ừhai v c a ph ng trình (1) cho hai v c a ph ng trình (2) ế ủ ươ ế ủ ươ đ đc ể ượ
m t ph ng trình m i d ngộ ươ ớ ạ : (x - y).k(x; y) = 0.
b/ Ví dụ: Gi i h ả ệ ph ng trình:ươ
( ) ( )
2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2 2 2
2 2 0 3 3 0
2 2 0 2 0
2 0 2 0 2 0
3x 3 1 0 0 3x 3 1 0
x x y x y x x y x y
y y x x y y x y x
x y x x y x x y x
hoac
x y y x y y
− = − − = − − + =
− = − + − = − − =
− − =
− − = − − =
− + − = − = + − =
1/
2 2 2
0
2 0 0
1
0
x y
x y x x x
x y
x y x y
= =
− − = − =
= =
− = =
2/
2
2
2
2 2
1 5 1 5
1 3 9 3 1 0
2 0
2 0 6 6
31 3
3x 3 1 0 1 5 1 5
1 3 36 6
3
xx x
x x
x x
x y x hoac
x
yy
xy y
y
+ −
−
= =
− − =
− − =
− − =
−
+ − = =− +
−
= =
=
K t lu n: V y h ph ng trình có 4 c p nghi m: ...................ế ậ ậ ệ ươ ặ ệ
c/ Bài t p áp d ng:ậ ụ Gi i các h ph ng trình sau:ả ệ ươ
1)
2
2
2 4 5
2 4 5
x y y
y x x
￬= - +￬
￬
￬
￬
￬= - +
￬
￬
￬
2)
2
2
2 3
2 3
y x
x y
￬= +
￬
￬
￬
￬
￬= +
￬
￬
￬
3)
2 2
2 2
2 7
2 7
x y x
y x y
￬- =
￬
￬
￬
￬
￬- =
￬
￬
￬
4)
2 2
2 2
2 3 3 1
2 3 3 1
x xy y x
y xy x y
￬- = - -￬
￬
￬
￬
￬- = - -
￬
￬
￬
5)
2
2
2
2
x y
y x
￬= -
￬
￬
￬
￬
￬= -
￬
￬
￬
6)
3
3
2 4
2 4
x y
y x
￬- =￬
￬
￬
￬
￬- =
￬
￬
￬
7)
2 2
2 2
2 3 2
2 3 2
x x y
y y x
￬- + =￬
￬
￬
￬
￬- + =
￬
￬
￬
8)
3
3
5
5
x x y
y y x
￬= +
￬
￬
￬
￬
￬= +
￬
￬
￬
9)
3
3
2
2
x y x
y x y
￬= -
￬
￬
￬
￬
￬= -
￬
￬
￬
10)
3
3
13 6
13 6
x x y
y y x
￬= -￬
￬
￬
￬
￬= -
￬
￬
￬
11)
2 3 2
2 3 2
4 3
4 3
y x x x
x y y y
￬= - +￬
￬
￬
￬
￬= - +
￬
￬
￬
12)
3
3
2 1
2 1
x y
y x
￬- =￬
￬
￬
￬
￬- =
￬
￬
￬
D ng 7: ạH ph ng trình đng c pệ ươ ẳ ấ :
2 2
0 (1)
( ; ) 0
ax bxy cy
f x y
+ + =
=
a/ Cách gi iả: Đt y = xt ặta đa ph ng trình đng c p (1) v d ng ph ng trình tích:ư ươ ẳ ấ ề ạ ươ
( )
2 2
0x at at c+ + =
b/ Ví dụ: Gi i h pt: ả ệ
2 2
2
2 0
2 3
x xy y
x y
+ − =
+ =
Đt y = xt ta có ặ
( )
2 2
1 2 0x t t+ − =
do x = 0 không ph i là nghi m nên ả ệ
2
2 1 0 1t t t− − = =
ho c ặ
0,5t= −
+) N u t = 1 ế
x = y
2
1 2
2 3 0 1; 1,5x x x x + − = = = −
.
+) N u t = -0,5 ế
-0,5x = y
2
3 4
2 6 0 1 7; 1 7x x x x + − = = − − = − +
. T đó tìm ừ
ra y.
c/ Bài t p áp d ng:ậ ụ Gi i các h ph ng trình sau:ả ệ ươ
1)
2 2
2
4 1
3 4
x xy y
y xy
￬- + =
￬
￬
￬
￬
￬- =
￬
￬
￬
2)
2 2
2
21
2 5 0
x xy y
y xy
￬- + =￬
￬
￬
￬
￬- + =
￬
￬
￬
3)
2 2
2 2
3 5 4 38
5 9 3 15
x xy y
x xy y
￬+ - =￬
￬
￬
￬
￬- - =
￬
￬
￬
4)
2 2
2 2
3 5
3 1
x y
x y
￬+ =￬
￬
￬
￬
￬- =
￬
￬
￬
5)
2 2
2 2
2 3 36
3 7 37
x y
x y
￬+ =￬
￬
￬
￬
￬+ =
￬
￬
￬
6)
2 2
2 2
2 3 9
2 2 2
x xy y
x xy y
￬+ + =￬
￬
￬
￬
￬+ + =
￬
￬
￬
7)
2 2
2 2
4 2 3
2 3 4
x xy y
x xy y
￬+ - =
￬
￬
￬
￬
￬- + =
￬
￬
￬
8)
2
2
3 54
4 115
x xy
xy y
￬+ =￬
￬
￬
￬
￬+ =
￬
￬
￬
9)
2 2
2
2 1
2
x y
xy x
￬- =￬
￬
￬
￬
￬+ =
￬
￬
￬
D ng 8: H ph ng trình không m u m cạ ệ ươ ẫ ự
*Dùng ph ng pháp gi i pt b c hai c a m t n, n còn l i coi là tham s .ươ ả ậ ủ ộ ẩ ẩ ạ ố
Ví dụ: Gi i h pt ả ệ
( )
2
2
1 0 (1)
2 1 0 (2)
x y x y
y xy
− − − =
− + =
(1) là pt b c 2 n x ta có: a - b + c = 1 + (y - 1) - y = 0 suy ra ậ ẩ
1 2
1; c
x x y
a
= − = =
+)V i x = -1 suy ra ớ
2
2 1 0 1y y y+ + = = −
.
+)V i x = y suy ra ớ
2 2 2
2 1 1 0 1y y y y− + = − = =
.
V y nghi m c a h là ậ ệ ủ ệ
( ) ( ) ( )
{ }
; 1; 1 , 1;1x y = − −
* Dùng tính ch t t ng các bình ph ng mà b ng 0.ấ ổ ươ ằ
Ví dụ: Gi i h pt ả ệ
3 3 3
3 0 (1)
3 (2)
x y z xyz
x y z
+ + − =
+ + =
(1)
( ) ( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
0,5 0 0x y z x y y z z x x y y z z x

+ + − + − + − = − + − + − =

(vì x +
y + z
0
) suy ra x = y = z k t h p v i (2) ta có x = y = z = 1.ế ợ ớ