
23 CHUYÊN ĐỀ
BỒI DƯỠNG HỌC SINH GIỎI LỚP 9
Tài liệu sưu tầm, ngày 31 tháng 5 năm 2021
1
Mục Lục
Trang
Chủ đề 1. Căn bậc 2, căn thức bậc 2
Chủ đề 2. Liên hệ phép nhân, phép chia và phép khai phương
Chủ đề 3. Biến đổi đơn giản biểu thức chứa căn bậc hai
Chủ đề 4. Căn bậc 3, căn bậc n
Chủ đề 5. Bất đẳng thức Cô - si
Chủ đề 6. Giải phương trình chứa ẩn trong căn
Chủ đề 7. Khái niệm về hàm số và đồ thị
Chủ đề 8. Hàm số bậc nhất và đồ thị
Chủ đề 9. Ứng dụng của hàm số bậc nhất để chứng minh bất đẳng thức
Chủ đề 10. Phương trình bậc nhất hai ẩn, hệ phương trình bậc nhất hai ẩn
Chủ đề 11. Phương pháp giải hệ phương trình bậc nhất hai ẩn
Chủ đề 12. Giải toán bằng cách lập hệ phương trình
Chủ đề 13. Hệ phương trình bậc nhất nhiều ẩn
Chủ đề 14. Hệ phương trình quy về hệ phương trình bậc nhất
Chủ đề 15. Hệ phương trình chứa tham số
Chủ đề 16. Phương trình bậc hai và công thức nghiệm
Chủ đề 17. Hệ thức Vi-et
Chủ đề 18. Phương trình quy về phương trình bậc hai
Chủ đề 19. Giải toán bằng cách lập phương trình
Chủ đề 20. Vị trí tương giao giữa parabol và đường thẳng
Chủ đề 21. Hệ phương trình bậc cao
Chủ đề 22. Phương trình vô tỷ
Chủ đề 23. Phương trình, hệ phương trình, bất phương trình không mẫu mực
Liên hệ tài liệ TÀI LIỆU TOÁN HỌC
Chương 1. CĂN BẬC HAI. CĂN BẬC BA
Chuyên đề 1. CĂN BẬC HAI, CĂN THỨC BẬC HAI
A. Kiến thức cần nhớ
1. Căn bậc hai số học
• Căn bậc hai số học của số thực a không âm là số không âm x mà
2
xa=
.
• Với
0a≥
( )
2
2
0x
xa x aa
≥
= ⇔ = =
Phép toán tìm căn bậc hai số học của một số gọi là phép khai phương.
Với hai số a, b không âm, thì ta có:
ab a b<⇔ <
.
2. Căn thức bậc hai
• Cho A là một biểu thức đại số, người ta gọi
A
là căn thức bậc hai của A, còn A được gọi là
biểu thức lấy căn hay biểu thức dưới dấu căn.
•
0A≥
xác định (hay có nghĩa) khi
0A≥
.
• Hằng đẳng thức
.
3. Chú ý
• Với
0a≥
thì:
2
xa xa=⇒=
2
xax a=⇒=±
.
•
( )
0 0A hay B
AB AB
≥≥
= ⇔ =
•
00A B AB+ =⇔==
.
B. Một số ví dụ
Ví dụ 1: So sánh các cặp số sau mà không dùng máy tính.
a)
10
và 3; b)
32
và
17
;
c)
35 15 1++
và
123
; d)
22+
và 2.
Giải
Tìm cách giải. Khi so sánh hai số
a
và
b
không dùng số máy tính, ta có thể:
• So sánh a và b
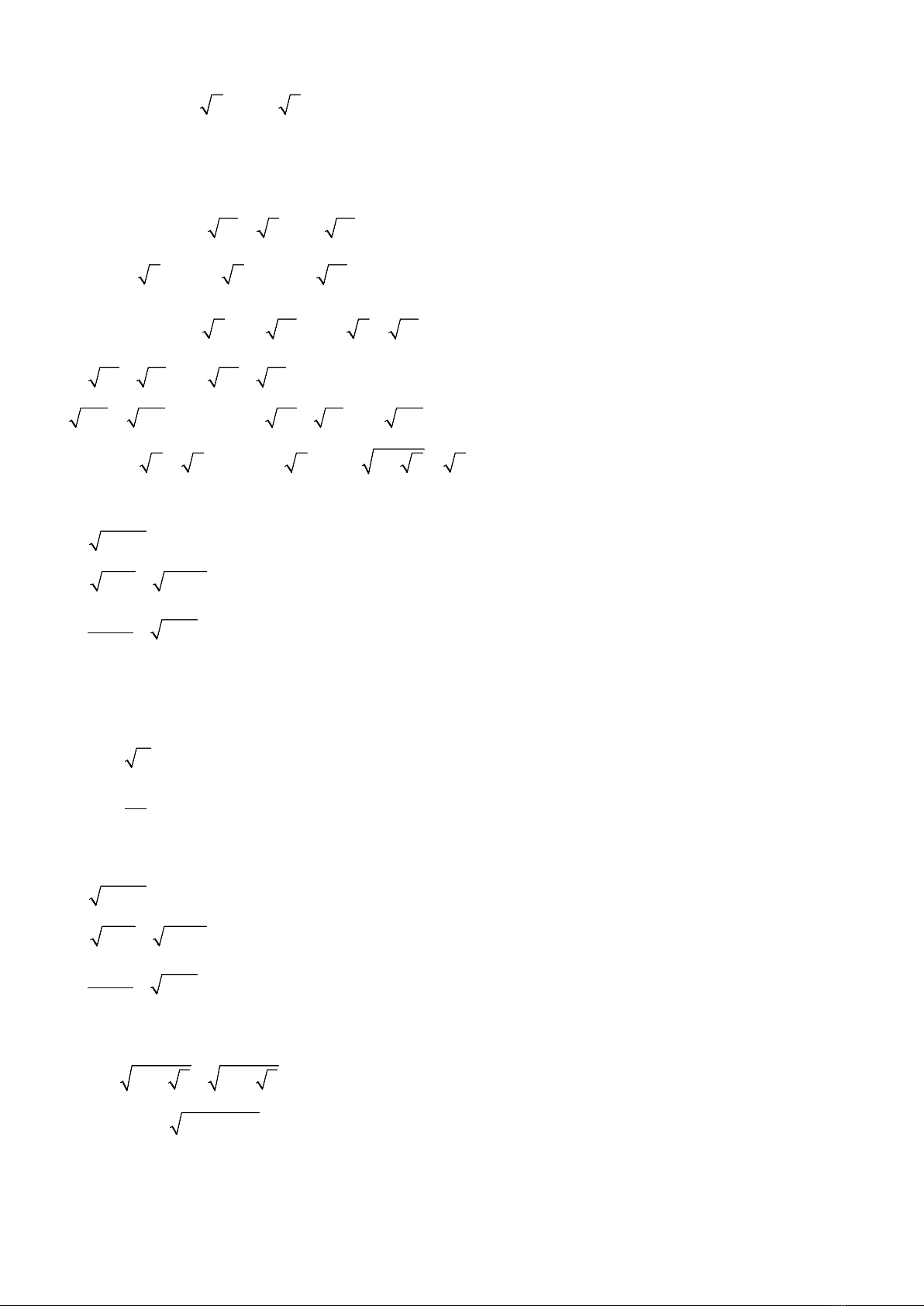
• So sánh
( )
2
a
và
( )
2
b
• Sử dụng kĩ thuật làm trội.
Trình bày lời giải
a) Ta có
10 9 10 9>⇒ >
nên
10 3>
.
b) Xét
( ) ( ) ( )
22 2
2
3 2 3 . 2 18; 17 17= = =
vì
18 17>
nên
( ) ( )
22
3 2 17 3 2 17> ⇒>
c)
35 15 1 36 16 1 6 4 1 11+ +< + += + +=
,
123 121 11>=
suy ra
35 15 1 123+ +<
.
d) Ta có
2 42 2 24 2 2 42<=⇒+<⇒+<=
.
Ví dụ 2: Tìm điều kiện để các biểu thức sau có nghĩa:
a)
82x+
;
b)
1 11xx−+ −
;
c)
2
3
9
xx
x++
−
.
Giải
Tìm cách giải. Để tìm điều kiện biểu thức có ý nghĩa, bạn lưu ý:
•
A
có nghĩa khi
0A≥
•
A
M
có nghĩa khi
0M≠
Trình bày lời giải
a)
82x+
có nghĩa khi
82 0 4xx+ ≥ ⇔ ≥−
.
b)
1 11xx−+ −
có nghĩa khi
10x−≥
và
11 0 1 11xx−≥ ⇔≤ ≤
.
c)
2
3
9
xx
x++
−
có nghĩa khi
30x+≥
và
29 0 3; 3x xx− ≠ ⇔ >− ≠
.
Ví dụ 3: Rút gọn biểu thức sau:
a)
6 25 6 25A=+ −−
;
b)
2
1 21Ba a a= +− − +
với
1a<
Giải
Tìm cách giải. Để rút gọn biểu thức chứa dấu căn, bạn nhớ rằng:
( )
2
21 1aa a± += ±
và lưu ý:
AB AB
AB BA AB
−≥
−=
−<
neáu
neáu
Trình bày lời giải
a) Ta có
6 25 6 25A=+ −−
5 25 1 5 25 1A= + +− − +
( ) ( )
22
51 51A= +− −
( ) ( )
51 51 2A= +− −=
.
b)
2
1 21Ba a a= +− − +
với
1a<
( )
2
11Ba a= +− −
( )
1 1 11 2Ba a a a a= +− − = +− − =
.
Ví dụ 4: Tìm giá trị nhỏ nhất của biểu thức sau:
a)
2
3 2 8 33A xx=+ −+
;
b)
2
8 18 1Bxx= −+−
;
c)
22 2
2 2 2 10 2 8 2020C x y xy x y y y= +− +−++ −+
.
Giải
a) Ta có:
( )
2
2
3 2 8 33 3 2 2 25 3 25 8A xx x=+ − + =+ − + ≥+ =
.
Vậy giá trị nhỏ nhất của biểu thức A là 8 khi
2x=
.
b) Ta có:
( )
2
2
8 181 4 21 21Bxx x= −+−= − +−≥ −
Vậy giá trị nhỏ nhất của biểu thức B là
21−
khi
4x=
.
c) Ta có:
22 2
2 2 2 10 2 8 2020C x y xy x y y y= +− +−++ −+
( ) ( )
22
1 9 2 2 2012C xy y⇒ = −+ ++ − +
9 2012 2015C⇒≥ + =
.
Vậy giá trị nhỏ nhất của C là 2015.
Khi
10 1
20 2
xy x
yy
− += =

⇔

−= =

.
Ví dụ 5: Tìm giá trị nhỏ nhất của biểu thức: