Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 9: Töông quan chuoãi
Ramu Ramanathan 1 Thuïc Ñoan/Haøo Thi
CHÖÔNG 9
Töông Quan Chuoãi
Phöông phaùp bình phöông toái thieåu ñaõ chöùng toû mang laïi caùc öôùc löôïng veà thoâng soá coù moät vaøi
tính chaát mong muoán, vôùi ñieàu kieän caùc soá haïng sai soá (ut) thoûa maõn moät soá giaû thieát. Ñaëc bieät,
caùc öôùc löôïng coù tính khoâng thieân leäch, nhaát quaùn, vaø hieäu quaû nhaát. Khi moät nhaø nghieân cöùu xöû
lyù döõ lieäu daïng chuoãi thôøi gian, moät soá vaán ñeà ñaëc bieät phaùt sinh thöôøng daãn ñeán keát quaû laø vi
phaïm vaøi giaû thieát caàn ñeå phaùt ra nhöõng tính chaát toát ñaõ lieät keâ. Trong chöông naøy, chuùng ta seõ
khaûo saùt moät daïng vi phaïm caùc giaû thieát cô baûn veà caùc soá haïng nhieãu. Thöù nhaát ta xem xeùt
nhöõng aån yù cuûa vieäc boû qua söï vi phaïm naøy vaø duøng thuû tuïc bình phöông toái thieåu thöôøng (OLS).
Ta coù theå kyø voïng raèng, nhö trong tröôøng hôïp phöông sai cuûa sai soá thay ñoåi, vaøi tính chaát coù
theå khoâng coøn giöõ ñöôïc nöõa. Thöù hai, ta kieåm ñònh söï coù maët cuûa söï vi phaïm naøy, vaø cuoái cuøng
thaûo luaän caùc phöông phaùp coù theå löïa choïn cho caùc vaán ñeà.
Giaû thieát 3.6 trong Chöông 3 phaùt bieåu raèng caùc soá haïng sai soá ut vaø us, cho caùc quan saùt
khaùc nhau t vaø s, laø phaân phoái ñoäc laäp. Tính chaát naøy goïi laø ñoäc laäp chuoãi. Töø Chöông 2, Phaàn
2.3, ut vaø us aån yù ñoäc laäp raèng chuùng khoâng töông quan. Khi moät nhaø nghieân cöùu ñang phaân tích
döõ lieäu chuoãi thôøi gian, giaû thieát naøy thöôøng seõ bò vi phaïm. Caùc soá haïng sai soá cho caùc thôøi ñoaïn
khoâng quaù caùch xa coù theå coù töông quan. Tính chaát naøy ñöôïc goïi laø töông quan chuoãi hay töï
töông quan (caùc thuaät ngöõ naøy seõ ñöôïc söû duïng thay theá nhau). Trong Chöông 3 ta ñaõ lieät keâ
moät soá nhaân toá giaûi thích cho söï coù maët cuûa soá haïng sai soá ut. Ñoù laø (1) caùc bieán bò loaïi boû, (2)
boû qua söï phi tuyeán, (3) caùc sai soá ño löôøng, vaø (4) hoaøn toaøn ngaãu nhieân, caùc taùc ñoäng khoâng
döï ñoaùn ñöôïc. Ba nhaân toá ñaàu tieân trong caùc nhaân toá naøy coù theå daãn ñeán caùc sai soá töông quan
chuoãi. Ví duï, giaû söû moät bieán phuï thuoäc Yt töông quan vôùi caùc bieán ñoäc laäp Xt1 vaø Xt2, nhöng nhaø
nghieân cöùu khoâng tính ñeán bieán Xt2 trong moâ hình. Taùc ñoäng cuûa bieán naøy seõ ñöôïc bao goäp qua
soá haïng sai soá ut. Bôûi vì nhieàu bieåu hieän chuoãi thôøi gian kinh teá coù chieàu höôùng theo thôøi gian,
Xt2 coù theå phuï thuoäc vaøo Xt-1,2, Xt-2,2, . . .. Ñieàu naøy seõ bieán thaønh söï töông quan roõ raøng giöõa ut
vaø ut-1, ut-2, . . ., do ñoù vi phaïm giaû thieát ñoäc laäp chuoãi. Vaäy, caùc chieàu höôùng trong caùc bieán bò
loaïi boû coù theå taïo söï töï töông quan trong caùc sai soá.
Töông quan chuoãi cuõng coù theå ñöôïc gaây neân bôûi ñaëc tröng sai veà daïng haøm soá. Ví duï, giaû
söû moái quan heä giöõa Y vaø X laø baäc hai nhöng ta giaû thieát laø ñöôøng thaúng. Vaäy soá haïng sai soá ut
seõ phuï thuoäc vaøo X2. Neáu X taêng hoaëc giaûm theo thôøi gian, ut cuõng seõ bieåu hieän chieàu höôùng nhö
vaäy, cho thaáy söï töï töông quan.
Sai soá coù heä thoáng trong ño löôøng cuõng gaây neân söï töï töông quan. Ví duï, giaû söû moät coâng
ty ñang caäp nhaät soá lieäu haøng hoùa toàn kho trong moät thôøi ñoaïn cho tröôùc. Neáu coù moät sai soùt coù
tính heä thoáng xaûy ra trong caùch ño löôøng, döï tröõ toàn kho tích luõy seõ phaûn aùnh caùc sai soá ño
löôøng tích luõy. Caùc sai soá naøy seõ cho thaáy nhö laø söï töông quan chuoãi.
Moät ví duï cuûa töông quan chuoãi, xeùt söï tieâu thuï ñieän theo caùc giôø khaùc nhau trong ngaøy.
Bôûi vì daïng thay ñoåi nhieät ñoä laø töông töï giöõa caùc thôøi ñoaïn lieân tieáp, ta coù theå kyø voïng daïng
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 9: Töông quan chuoãi
Ramu Ramanathan 2 Thuïc Ñoan/Haøo Thi
tieâu thuï laø töông quan giöõa caùc thôøi ñoaïn laân caän. Neáu moâ hình khoâng ñöôïc ñaëc tröng moät caùch
thích hôïp, taùc ñoäng naøy coù theå ñeå loä söï töông quan cao giöõa caùc sai soá töø caùc thôøi ñoaïn gaàn keà.
Moät ví duï khaùc cuûa töông quan chuoãi ñöôïc tìm thaáy trong döõ lieäu thò tröôøng chöùng khoaùn. Giaù
cuûa moät chöùng khoaùn ñaëc bieät naøo ñoù hoaëc moät chæ soá thò tröôøng chöùng khoaùn taïi thôøi ñieåm
ñoùng cöûa cuûa nhöõng ngaøy lieân tieáp hoaëc trong nhöõng giôø lieân tieáp coù theå töông quan theo chuoãi.
} VÍ DUÏ 9.1
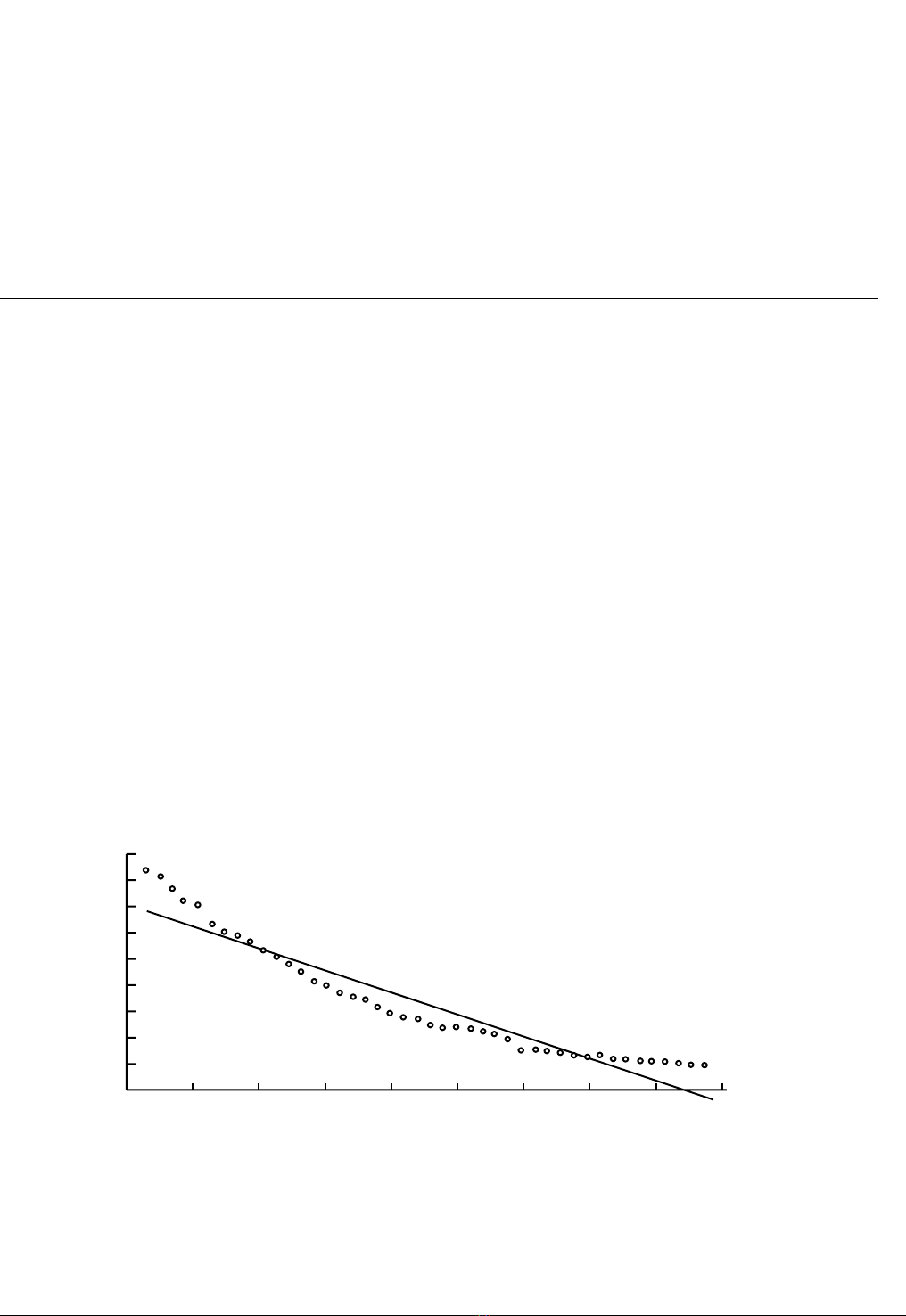
DATA6-6 coù döõ lieäu haøng naêm veà daân soá noâng traïi theo phaàn traêm toång daân soá taïi Myõ. Hình
9.1 laø ñoà thò cuûa daân soá noâng traïi vaø giaù trò phuø hôïp thu ñöôïc töø xu höôùng thôøi gian tuyeán tính
cuûa daïng haøm FARMPOP = α + β TIME + u, trong ñoù TIME laø t töø 1 ñeán 44. Phaàn Maùy Tính
Thöïc Haønh 9.1 coù caùc höôùng daãn ñeå chaïy laïi ví duï naøy. Töø bieåu ñoà ta löu yù raèng trong nhöõng
thôøi ñoaïn ban ñaàu thì caùc giaù trò thöïc teá naèm phía treân ñöôøng bình phöông toái thieåu, trong
nhöõng thôøi ñoaïn giöõa caùc ñieåm phaân taùn tuï hoïp ôû phía döôùi ñöôøng thaúng, vaø trong caùc thôøi
ñoaïn sau cuøng chuùng laïi nhaát quaùn naèm phía treân ñöôøng thaúng. Do ñoù ta kyø voïng söï töông
quan cao giöõa caùc sai soá cuûa caùc thôøi ñoaïn lieân tieáp vaø gaàn keà nhau, nhö vaäy vi phaïm giaû thieát
ñoäc laäp chuoãi. Thöïc teá, heä soá töông quan giöõa ut vaø ut-1 laø 0,97. Moät phöông caùch höõu duïng ñeå
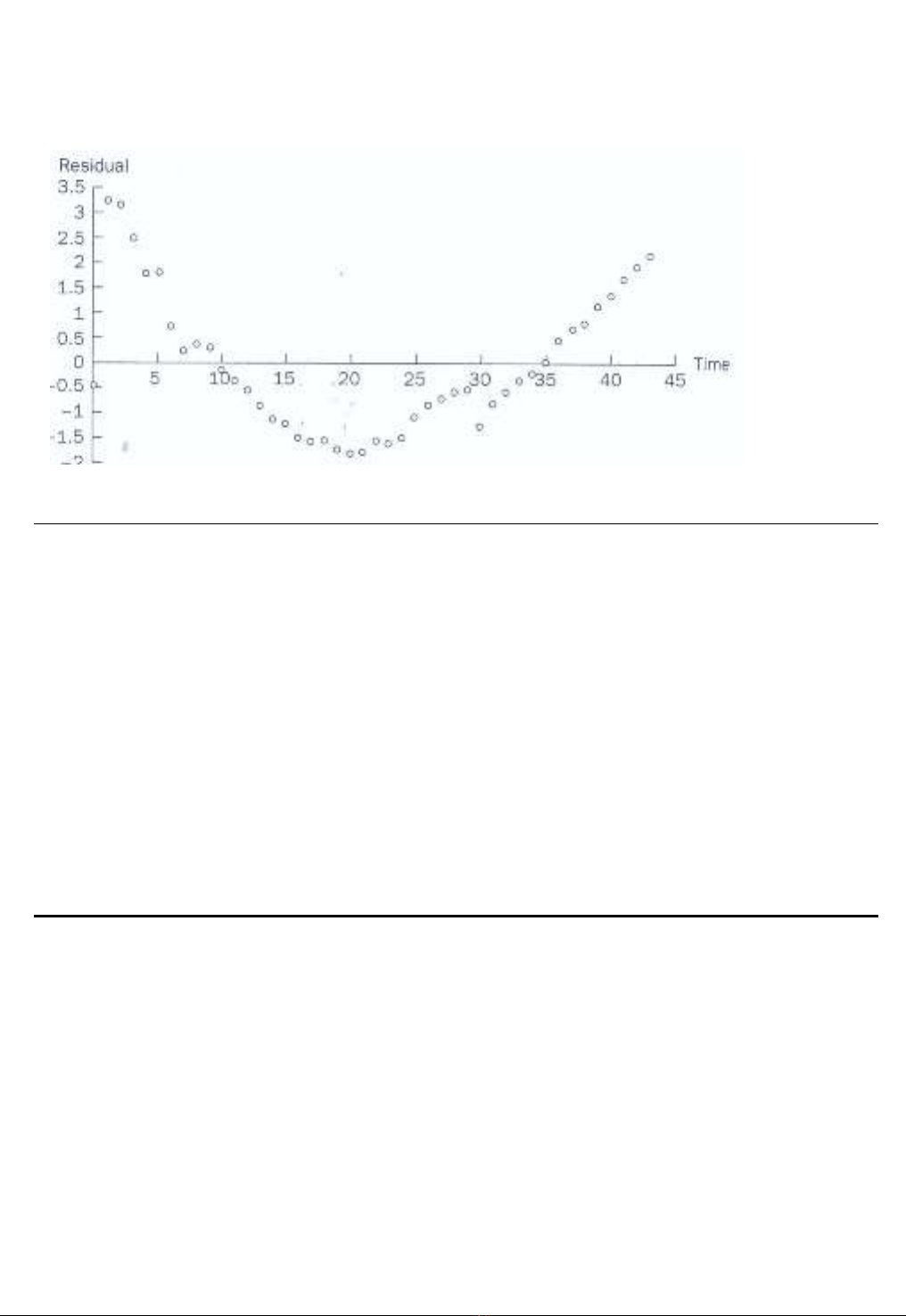
nhaän daïng söï coù maët cuûa töông quan chuoãi laø bieåu ñoà phaàn dö. Ñaây ñôn giaûn laø moät ñoà thò cuûa
caùc soá dö öôùc löôïng ut theo thôøi gian t, Hình 9.2 minh hoïa bieåu ñoà soá dö naøy cho tröôøng hôïp
daân soá noâng traïi. Ta quan saùt thaáy moät xu höôùng roõ raøng caùc phaàn dö lieân tieáp tuï taäp veà moät
phía cuûa ñöôøng thaúng soá khoâng hoaëc phía kia. Ñaây laø moät daáu hieäu theo daïng ñoà thò cho thaáy
söï coù maët cuûa töï töông quan. Neáu ut laø ñoäc laäp, söï tuï hoïp naøy coù theå seõ khoâng xaûy ra.
} Hình 9.1 Minh Hoïa cuûa Töï Töông Quan
0 5 10 15 20 25 30 35 40 45
18
16
14
12
10
8
6
4
2
0
Time
Farmpop
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 9: Töông quan chuoãi
Ramu Ramanathan 3 Thuïc Ñoan/Haøo Thi
} Hình 9.2 Minh Hoïa cuûa Bieåu Ñoà Phaàn Dö
Töø söï thaûo luaän vaø caùc ví duï naøy roõ raøng söï töï töông quan thöïc söï vi phaïm Giaû thieát 3.6.
Baây giôø ta tieáp tuïc thaûo luaän caùc heä quaû khi boû qua söï töï töông quan, trình baøy caùc kieåm ñònh
thích hôïp ñeå nhaän daïng söï coù maët cuûa töông quan chuoãi, vaø cuoái cuøng thaûo luaän caùc phöông
phaùp öôùc löôïng coù theå choïn löïa.
} 9.1 Töông Quan Chuoãi Baäc Nhaát
Ñaàu tieân, ta xeùt tröôøng hôïp ñaëc bieät nhaát cuûa töông quan chuoãi goïi laø töông quan chuoãi baäc
nhaát. Maëc duø ta duøng moâ hình hoài qui tuyeán tính ñôn ñeå khaûo saùt caùc vaán ñeà, taát caû keát quaû
cuõng khaùi quaùt hoùa cho tröôøng hôïp hoài qui boäi. Neáu töông quan chuoãi toàn taïi, thì Cov(ut, us) ≠
0 vôùi t ≠ s, nghóa laø, sai soá cho thôøi ñoaïn t laø töông quan vôùi sai soá cho thôøi ñoaïn s. Giaû thieát
cuûa töï töông quan baäc nhaát ñöôïc phaùt bieåu chính thöùc nhö sau:
GIAÛ THIEÁT 9.1
Y
t = α + βXt + ut (9.1)
ut = ρut-1 + εt –1 < ρ < 1 (9.2)
Vaäy sai soá ut quan heä vôùi sai soá cuûa thôøi ñoaïn tröôùc (ut-1), moät soá haïng sai soá môùi (εt), vaø
moät thoâng soá môùi ρ, ρ phaûi coù trò tuyeät ñoái nhoû hôn 1, neáu khoâng, taùc ñoäng buøng noå coù theå xaûy
ra. Bôûi vì ρ laø heä soá cuûa soá haïng sai soá treã moät thôøi ñoaïn, ñöôïc goïi laø heä soá töï töông quan baäc
nhaát. Quaù trình ñöôïc moâ taû bôûi Phöông trình (9.2) ñöôïc goïi laø quaù trình töï hoài qui baäc nhaát,
ñöôïc bieát ñeán phoå bieán hôn laø AR(1). Sau naøy trong chöông naøy (Phaàn 9.5) ta xeùt caùc quaù
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 9: Töông quan chuoãi
Ramu Ramanathan 4 Thuïc Ñoan/Haøo Thi
trình töï hoài qui baäc cao hôn. Caùc sai soá môùi εt ñöôïc giaû thieát ñeå thoûa maõn caùc ñieàu kieän sau
ñaây:
GIAÛ THIEÁT 9.2
Caùc sai soá εt tuaân theo phaân phoái moät caùch ñoäc laäp vaø ñoàng nhaát vôùi trò trung bình laø 0 vaø
phöông sai khoâng ñoåi sao cho E(εt) = 0, E(ε2t) = σ2ε < ∞, vaø E(εtεt-s) = 0 vôùi s ≠ 0.
Vaäy caùc soá haïng sai soá môùi ñöôïc giaû thieát ñeå coù cuøng tính chaát vôùi caùc tính chaát maø thuû
tuïc OLS giaû thieát ut phaûi coù. Trong taøi lieäu chuoãi thôøi gian, moät chuoãi tuaân theo Giaû thieát 9.2
ñöôïc goïi laø chuoãi coù tính nhieãu traéng vôùi trò trung bình laø 0. Bôûi vì ut phuï thuoäc vaøo ut-1, ta coù
theå kyø voïng laø chuùng töông quan. Löu yù raèng ut khoâng phuï thuoäc tröïc tieáp vaøo ut-2; tuy nhieân,
laïi phuï thuoäc giaùn tieáp qua ut-1 bôûi vì ut-1 phuï thuoäc tröïc tieáp vaøo ut-2. Vaäy, ut töông quan vôùi taát
caû sai soá quaù khöù. Neáu ñoàng phöông sai laø döông, thì coù töï töông quan döông, vaø khi ñoàng
phöông sai aâm, ta coù töï töông quan aâm. Trong Phuï luïc Phaàn 9.A.2 cho thaáy Cov(ut, ut-1) = σ2ρs,
vôùi s ≥ 0.
} 9.2 Caùc Heä Quaû khi Boû Qua Töông Quan Chuoãi
Trong Chöông 3 ta ñaõ chöùng minh raèng theo Giaû thieát 3.3 vaø 3.4, (nghóa laø ut coù trò trung bình
laø 0 vaø khoâng töông quan vôùi Xt), caùc öôùc löôïng OLS laø khoâng thieân leäch vaø nhaát quaùn. Vì söï
chöùng minh caùc tính chaát naøy khoâng phuï thuoäc vaøo Giaû thieát 3.6, giaû thieát bò vi phaïm bôûi söï coù
maët cuûa töï töông quan, caùc öôùc löôïng OLS (vaø caùc döï baùo döïa treân chuùng) laø khoâng thieân leäch
vaø nhaát quaùn ngay caû khi caùc soá haïng sai soá töông quan theo chuoãi. Vaán ñeà laø söï hieäu quaû cuûa
caùc öôùc löôïng. Trong chöùng minh ñònh lyù Gauss-Markov ñaõ thieát laäp söï hieäu quaû (Phaàn 3.A.4),
moät trong caùc böôùc lieân quan vieäc cöïc tieåu phöông sai cuûa toå hôïp tuyeán tính ∑atut:
(
)
∑
∑
∑∑ ≠
+σ=
st
stst
22
ttt )u,u(CovaaauaVar (9.3)
trong ñoù toång keùp laø theo moïi t vaø s coù giaù trò khaùc nhau. Neáu Cov(ut, us) ≠ 0, soá haïng thöù hai
beân tay phaûi seõ khoâng trieät tieâu. Do vaäy, cöïc tieåu ∑at2σ2 (seõ ñöa ra caùc phöông trình chuaån
OLS) khoâng töông ñöông vôùi vieäc cöïc tieåu Phöông trình (9.3). Vì lyù do naøy, öôùc löôïng khoâng
thieân leäch tuyeán tính toát nhaát (BLUE) cöïc tieåu phöông trình (9.3) seõ khoâng gioáng nhö öôùc
löôïng OLS. Noùi caùch khaùc, öôùc löôïng OLS khoâng phaûi BLUE vaø do vaäy khoâng hieäu quaû. Vaäy,
heä quaû khi boû qua söï töï töông quan gioáng nhö khi boû qua phöông sai cuûa sai soá thay ñoåi; nghóa
laø caùc döï baùo vaø öôùc löôïng laø khoâng thieân leäch vaø nhaát quaùn nhöng khoâng hieäu quaû. Tuy nhieân,
coù moät ñieàu neân bieát tröôùc. Neáu caùc bieán X coù bao goàm moät bieán phuï thuoäc coù hieäu öùng treã
nhö Yt-1 thì töông quan chuoãi seõ cho ra caùc öôùc löôïng OLS khoâng nhaát quaùn. Ñieàu naøy ñöôïc
chöùng minh trong chöông keá tieáp.
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 9: Töông quan chuoãi
Ramu Ramanathan 5 Thuïc Ñoan/Haøo Thi
Ta coù theå cho thaáy raèng neáu töông quan chuoãi trong ut laø döông vaø bieán ñoäc laäp Xt taêng
leân theo thôøi gian (tröôøng hôïp thöôøng thaáy), thì phöông sai phaàn dö öôùc löôïng ( 2
ˆ
σ) seõ laø moät
öôùc löôïng quaù thaáp vaø giaù trò cuûa R2 seõ laø moät öôùc löôïng quaù cao. Noùi caùch khaùc, ñoä thích hôïp
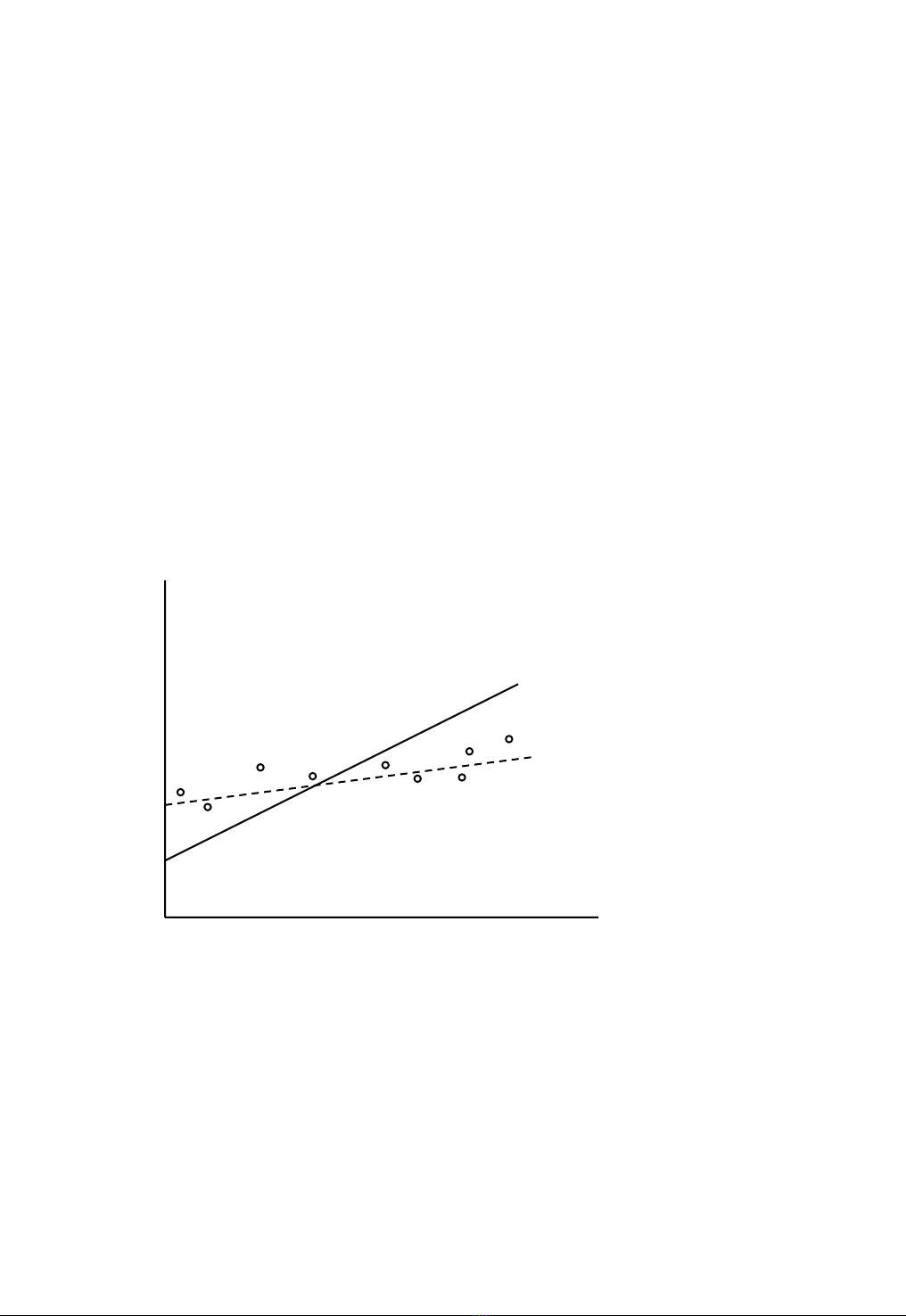
seõ bò phoùng ñaïi vaø caùc sai soá chuaån öôùc löôïng seõ nhoû hôn caùc sai soá chuaån thöïc söï. Caùc ñieåm
naøy ñöôïc minh hoïa trong Hình 9.3, moät bieåu ñoà phaân taùn tieâu bieåu, vôùi söï trôï giuùp cuûa moâ hình
hoài qui ñôn. Ñöôøng ñaäm laø ñöôøng hoài qui “thöïc” α+βX. Giaû söû coù töï töông quan döông; nghóa
laø, ñoàng phöông sai giöõa hai soá haïng nhieãu ngaãu nhieân lieân tieáp laø döông. Giaû söû theâm raèng
ñieåm phaân taùn ñaàu tieân (X1, Y1) naèm phía treân ñöôøng hoài qui thöïc. Ñieàu naøy nghóa laø u1 seõ
döông. Bôûi vì u2 vaø u1 laø töông quan döông, u2 coù theå döông, laøm cho (X2, Y2) cuõng naèm phía
treân ñöôøng thaúng. Do ñoù, moät vaøi ñieåm phaân taùn ñaàu tieân coù theå naèm phía treân ñöôøng hoài qui
thöïc. Giaû söû moät trong caùc ñieåm phaân taùn ngaãu nhieân naèm phía döôùi ñöôøng hoài qui thöïc bôûi do
baûn chaát ngaãu nhieân cuûa caùc soá haïng u. Nhö vaäy moät vaøi ñieåm keá tieáp cuõng coù theå naèm phía
döôùi ñöôøng hoài qui thöïc.
} Hình 9.3 Öôùc Löôïng Quaù Thaáp cuûa Phöông Sai Phaàn Dö
Bôûi vì thuû tuïc bình phöông toái thieåu laøm cöïc tieåu toång bình phöông caùc ñoä leäch, ñöôøng
“thích hôïp” seõ troâng nhö ñöôøng ñöùt neùt. Phöông sai thöïc cuûa caùc sai soá ñöôïc xaùc ñònh bôûi ñoä
leäch cuûa (Xt, Yt) so vôùi ñöôøng hoài qui thöïc, roõ raøng seõ lôùn hôn phöông sai phaàn dö öôùc löôïng,
ñöôïc tính töø caùc ñoä leäch xung quanh ñöôøng thích hôïp. Do ñoù, toång bình phöông sai soá tính toaùn
(ESS) seõ nhoû hôn giaù trò thöïc, vaø R2seõ lôùn hôn giaù trò thöïc.
Trong tröôøng hôïp toång quaùt, caùc phöông sai cuûa caùc heä soá hoài qui seõ bò thieân leäch. Ñeå
bieát theâm phaân tích chi tieát baûn chaát cuûa thieân leäch, baïn ñoïc coù quan taâm neân tham khaûo Phaàn
8.3 saùch cuûa Kmenta (1986).
Ñöôøng “thöïc”
(“true” line)
Ñöôøng “thích hôïp”
(“fitted” line)
Y
X