Chương 9 ỔN ĐỊNH
THANH CHỊU NÉN ĐÚNG
TÂM
9.1 Khái niệm
9.2 Điều kiện ổn định và tính toán ổn định
9.3 Hình dáng hợp lý khi chịu nén
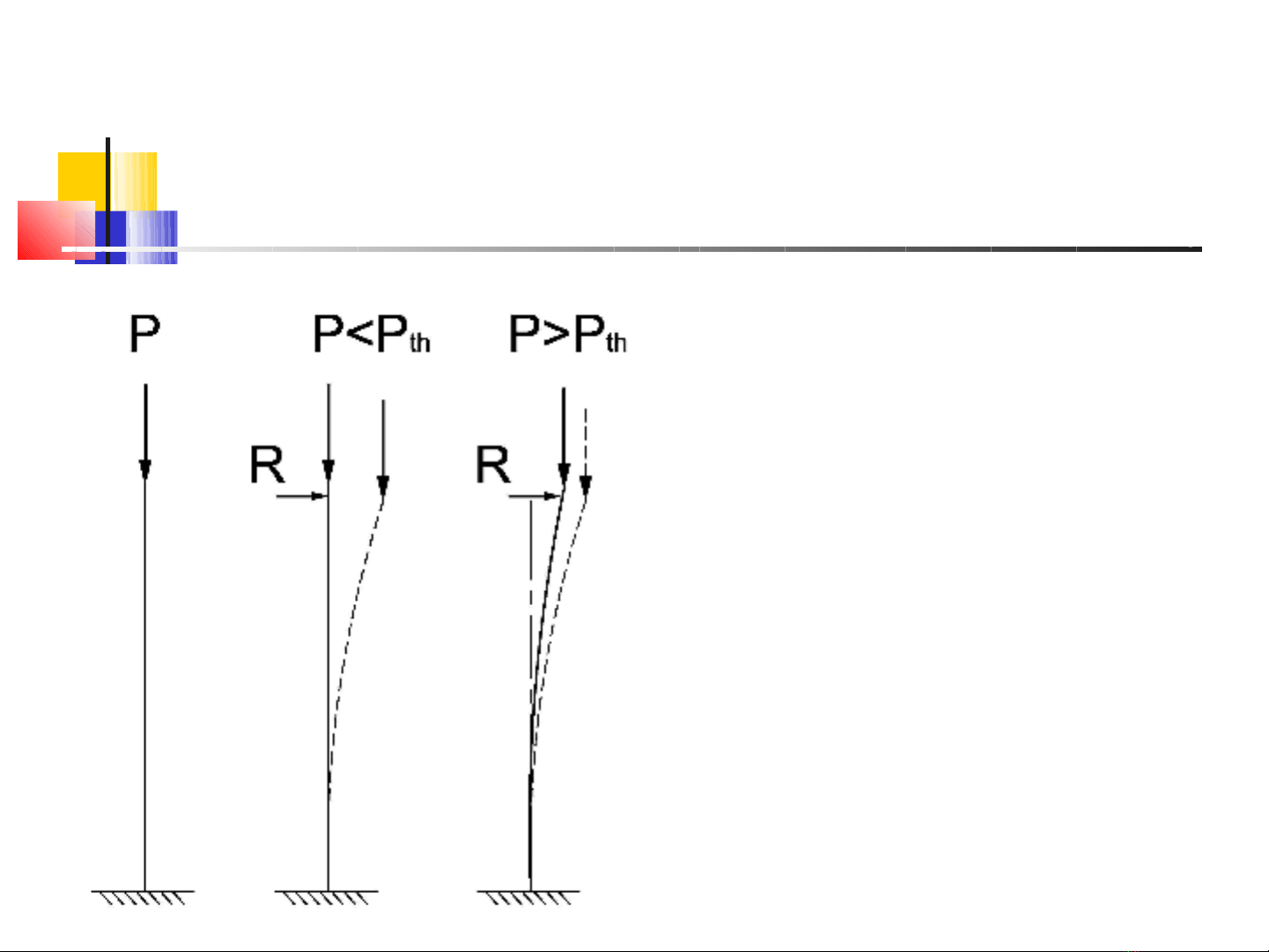
9.1 Khái niệm
Trạng thái cân bằng
ổn định
Trạng thái tới hạn
Trạng thái cân bằng
không ổn định
(trạng thái mất ổn
định)
9.1 Khái niệm
Khi mất ổn định, công trình hay chi tiết máy
làm việc không bình thường.
Khi vượt quá tr.thái tới hạn, công trình hay chi
tiết có thể bị phá hoại một cách bất ngờ vì biến
dạng tăng rất nhanh. Khi thiết kế cần đảm bảo:
độ bền, độ cứng và độ ổn định, nên
Giải b.toán ổn định là phải xác định Pth
ôđ
th
k
P
P
≤
9.2 Điều kiện ổn định
- Tính toán ổn định
Xác định lực tới hạn của thanh chịu nén
đúng tâm (bài toán Ơle)- Tính ổn định
trong miền đàn hồi.
Tính ổn định ngoài miền đàn hồi
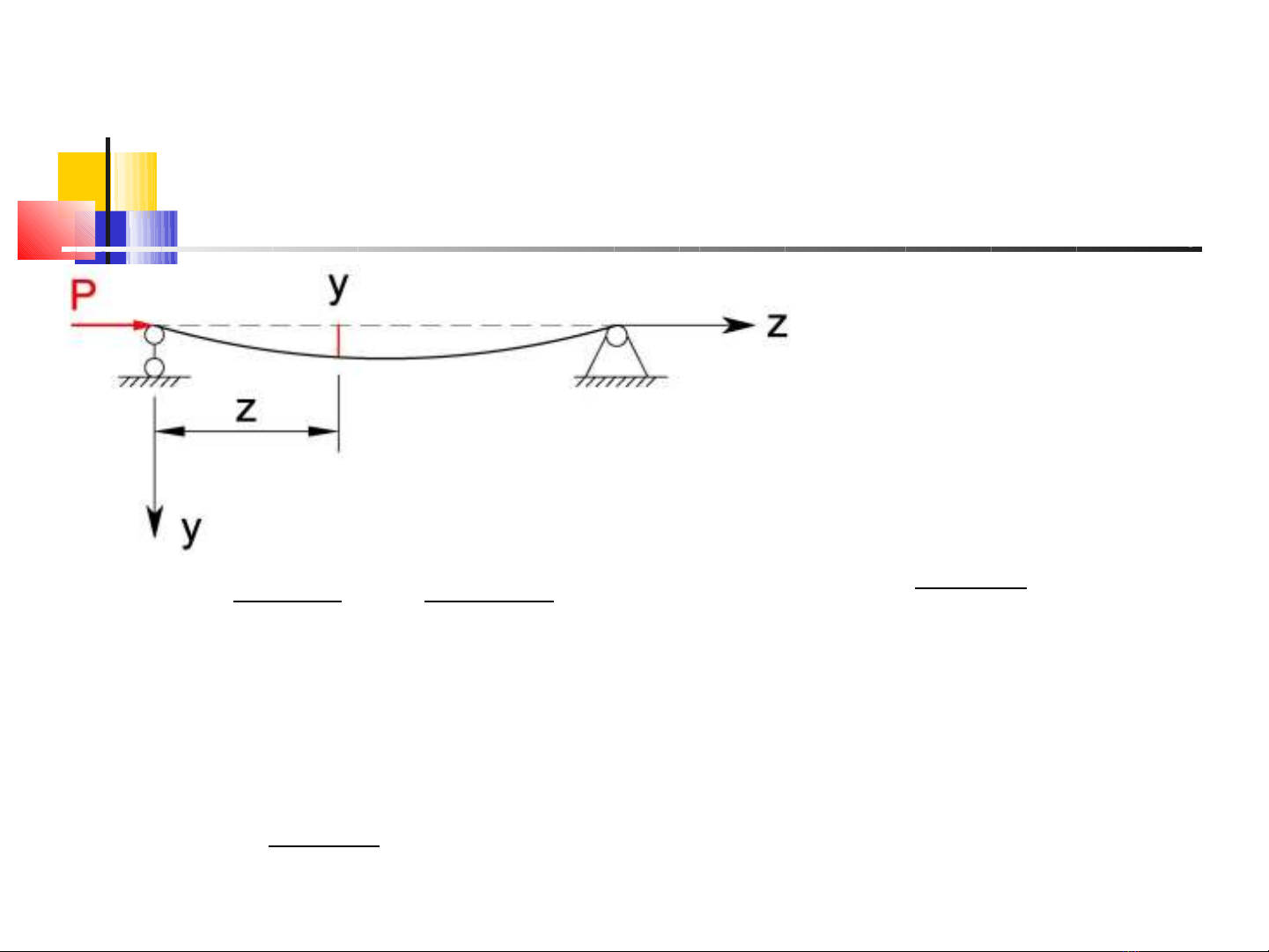
Xác định lực tới hạn của thanh
chịu nén đúng tâm (bài toán Ơle)
( ) ( )
zyPzM
th
=
( ) ( ) ( )
minmin
"EJ
zyP
EJ
zM
zy
th
−=−=
( ) ( )
0"
min
=+⇒
zy
EJ
P
zy
th
( ) ( )
0"
2
=+⇒
zyzy
α
( )
zCzCzy
21
α+α=
cossin
min
2
EJ
P
th
=
α