-E4*E5-G4*G5-I4*I5
ÔN T P PH NG PHÁP T A Đ TRONG KHÔNG GIANẬ ƯƠ Ọ Ộ
3. M t c uặ ầ
4. Ph ng trình m t ươ ặ
ph ngẳ
5. Ph ng trình đ ng ươ ườ
th ng trong không gianẳ
6. M t s bài toánộ ố
2. T a đ vect & đi m ọ ộ ơ ể
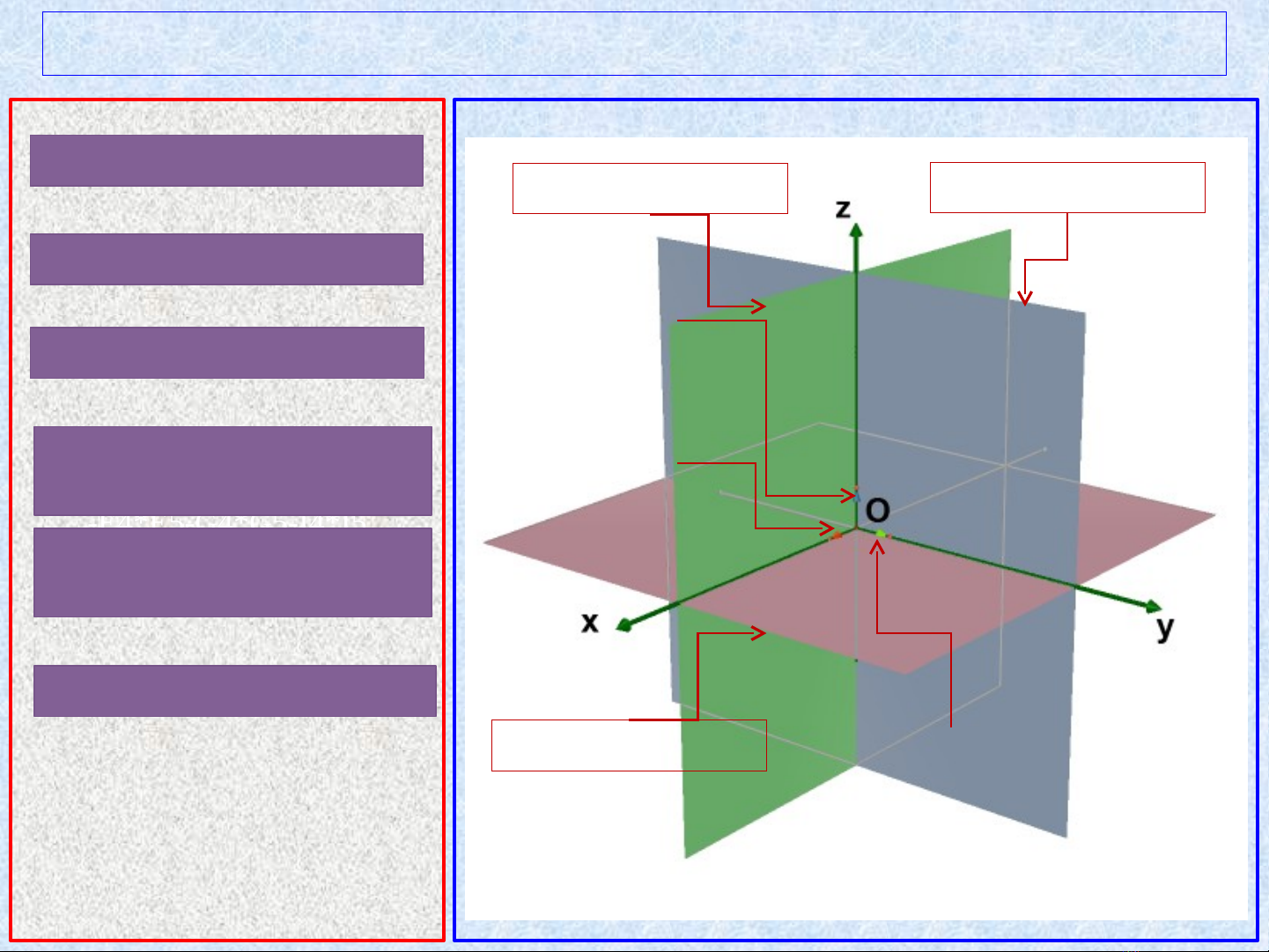
1. H tr c t a đ Oxyzệ ụ ọ ộ
H i đ ng b môn Toánộ ồ ộ
T nh Đ ng Thápỉ ồ
Võ Thanh Hùng
ÔN T P PH NG PHÁP T A Đ TRONG KHÔNG GIANẬ ƯƠ Ọ Ộ
-E4*E5-G4*G5-I4*I5
M t ph ng (Oxy) ặ ẳ
M t ph ng (Oyz) ặ ẳ
M t ph ng (Oxz) ặ ẳ
3. M t c uặ ầ
4. Ph ng trình m t ươ ặ
ph ngẳ
5. Ph ng trình đ ng ươ ườ
th ng trong không gianẳ
6. M t s bài toánộ ố
2. T a đ vect & đi m ọ ộ ơ ể
1. H tr c t a đ Oxyzệ ụ ọ ộ
ÔN T P PH NG PHÁP T A Đ TRONG KHÔNG GIANẬ ƯƠ Ọ Ộ
Các công th c liên quan đ n t a đ vectứ ế ọ ộ ơ:
Các công th c liên quan đ n t a đi mứ ế ọ ể :
-E4*E5-G4*G5-I4*I5
3. M t c uặ ầ
4. Ph ng trình m t ươ ặ
ph ngẳ
5. Ph ng trình đ ng ươ ườ
th ng trong không gianẳ
6. M t s bài toánộ ố
2. T a đ vect & đi m ọ ộ ơ ể
1. H tr c t a đ Oxyzệ ụ ọ ộ
ÔN T P PH NG PHÁP T A Đ TRONG KHÔNG GIANẬ ƯƠ Ọ Ộ
Ph ng trình m t c uươ ặ ầ :
Đi u ki n ph ng trình m t c uề ệ ươ ặ ầ :
Ti p di n c a m t c uế ệ ủ ặ ầ :
M t ph ng () là ti p di n c a ặ ẳ ế ệ ủ
m t c u S(I; R) khi và ch khi ặ ầ ỉ
d(I,()) = R
Ti p di n c a m t c u (S) ế ệ ủ ặ ầ
vuông góc v i bán kính t i ti p ớ ạ ế
đi mể
-E4*E5-G4*G5-I4*I5
3. M t c uặ ầ
4. Ph ng trình m t ươ ặ
ph ngẳ
5. Ph ng trình đ ng ươ ườ
th ng trong không gianẳ
6. M t s bài toánộ ố
2. T a đ vect & đi m ọ ộ ơ ể
1. H tr c t a đ Oxyzệ ụ ọ ộ
-E4*E5-G4*G5-I4*I5
ÔN T P PH NG PHÁP T A Đ TRONG KHÔNG GIANẬ ƯƠ Ọ Ộ
Ph ng trình m t ph ngươ ặ ẳ :
Vect pháp tuy n c a m t ph ngơ ế ủ ặ ẳ :
Vect pháp tuy n c a m t ph ng (P) là vect khác ơ ế ủ ặ ẳ ơ
vect - không và có giá vuông góc m t ph ng (P).ơ ặ ẳ
3. M t c uặ ầ
4. Ph ng trình m t ươ ặ
ph ngẳ
5. Ph ng trình đ ng ươ ườ
th ng trong không gianẳ
6. M t s bài toánộ ố
2. T a đ vect & đi m ọ ộ ơ ể
1. H tr c t a đ Oxyzệ ụ ọ ộ