
TRÇN QUANG THANH-K15-CAO HäC Lý -§H VINH
1
PH¦¥NG PH¸P DïNG §¦êNG TRßN L¦îNG GI¸C øNG DôNG GI¶I BµI TËP
DAO §éNG §IÒU HßA
§Æt vÊn ®Ò: Nh− chóng ta ®· biÕt viÖc gi¶i c¸c bµi tËp trong vËt lý phÇn d®®h cña
con l¾c lß xo, con l¾c ®¬n nãi chung lµ cã nhiÒu c¸ch. Tïy thuéc vµo tõng ng−êi tõng bµi
to¸n cô thÓ mµ dïng c¸ch nµy hay c¸ch kh¸c. Riªng phÇn bµi tËp x¸c ®Þnh thêi ®iÓm vËt
®i qua vÞ trÝ cho tr−íc trªn quü ®¹o vµ kho¶ng thêi gian ng¾n nhÊt ®Ó vËt ®i tõ vÞ trÝ x
1
®Õn
vÞ trÝ x
2
hoÆc x¸c ®ùng pha ban ®Çu cña dao ®éng lµ d¹ng bµi tËp ®iÓn h×nh mµ ta cã thÓ
dïng Ýt nhÊt lµ hai c¸ch. §ã lµ ph−¬ng ph¸p l−îng gi¸c vµ ph−¬ng ph¸p vÏ ®−êng trßn
l−îng gi¸c. víI ph−¬ng ph¸p ®Çu th× phï hîp víi kiÓu lµm bµi tù luËn, nh−ng trong thêi
®iÓm hiÖn nay khi ph¶i lµm quen víi h×nh thøc thi tr¾c nghiÖm th× cÇn 1 ph−¬ng ¸n tèi
−u kh¸c nhanh h¬n vµ hiÖu qu¶ h¬n. Víi tinh thÇn ®ã t«i xin m¹nh d¹n ®−a ra ph−¬ng
ph¸p gi¶i b»ng c¸ch dïng ®−êng trßn l−îng gi¸c. Hy väng phÇn nµo ®ã gióp c¸c b¹n
häc sinh ®ang «n thi TN-C§-§H cã mét ph−¬ng tiÖn, c«ng cô h÷u Ých. Mäi th¾c m¾c, ý
kiÕn trao ®æi xin göi vÒ theo ®Þa chØ thanh17802002@yahoo.com hoÆc 0904.727271 hoÆc
038.3590194. Xin ch©n thµnh c¶m ¬n
C¥ Së Lý THUYÕT: Dùa vµo mèi liªn hÖ gi÷a chuyÓn ®éng trßn ®Òu vµ D§§H th×
kho¶ng thêi gian cÇn tÝnh ®−îc x¸c ®Þnh theo c«ng thøc :
ω
α
=
min
t
ChiÒu quay cña vËt quy −íc quay ng−îc chiÒu kim ®ång hå(nh− HV)
Víi
α
lµ gãc mµ vËt quÐt ®−îc khi chuyÓn ®éng tõ vÞ trÝ x
1
®Õn vÞ trÝ x
2
trªn trôc ox
vµ t−¬ng øng trªn cung trßn nh− h×nh vÏ sau :
x
ω
Ta coi vËt chuyÓn ®éng trªn trôc ox tõ vÞ trÝ x
1
®Õn vÞ trÝ A +
x
2
t−¬ng øng trªn vßng trßn vËt quÐt ®−îc cung MN
x¸c ®Þnh b»ng gãc
α
. N
∆
M
-A
Th«ng th−êng
m
K
f
T=== .2
2
π
π
ω
hoÆc bµi ra cho tr−íc. NhiÖm vô cßn l¹i cña
chóng ta lµ x¸c ®Þnh gãc quÐt
α
. §Ó tÝnh gãc quÐt
α
cã c¸c tr−êng hîp x¶y ra nh−
sau :
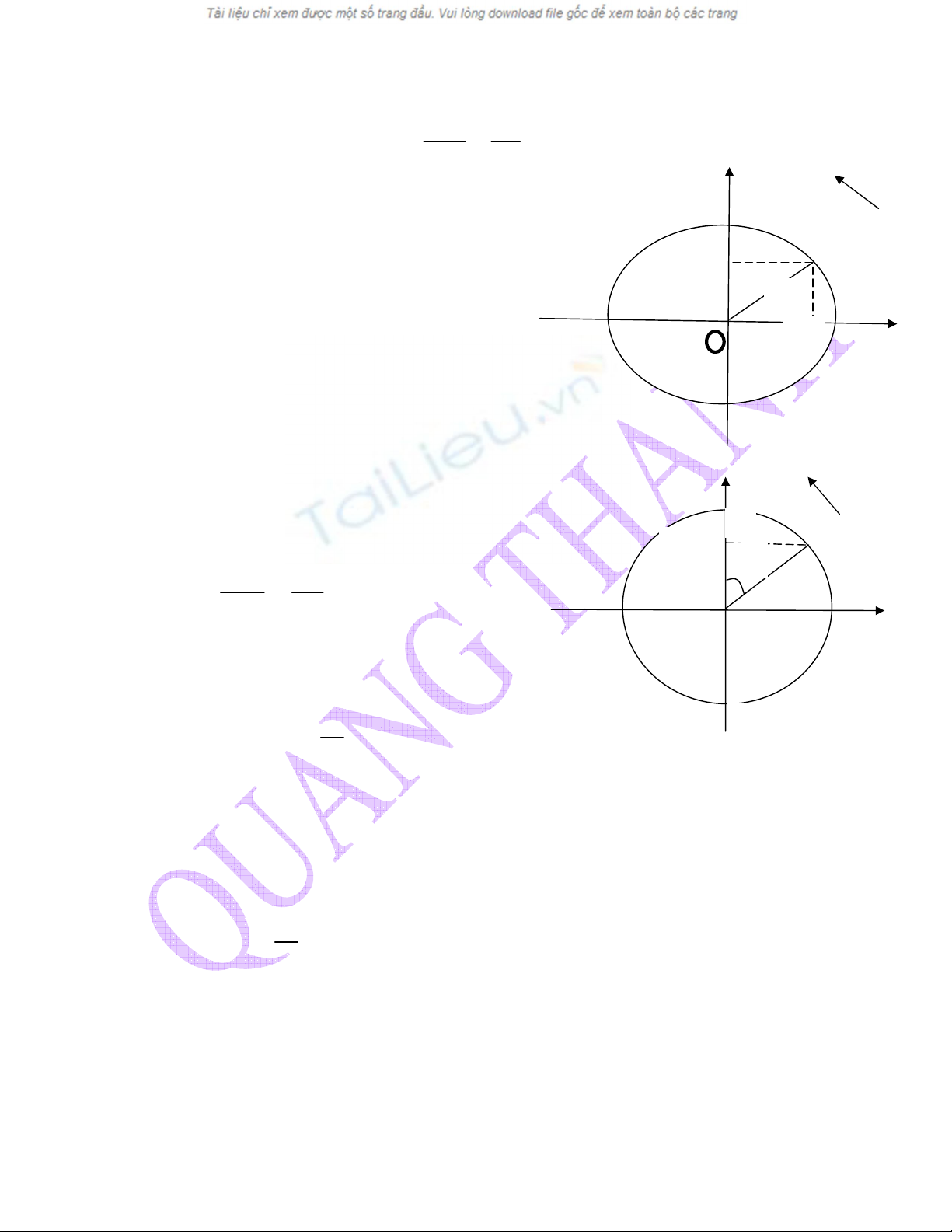
TH 1: Khi vËt ®i tõ VTCB ®Õn vÞ trÝ cã täa ®é x
1
(d−¬ng) th× t−¬ng øng trªn ®−êng trßn
vËt quÐt ®−îc gãc
α
nh− h×nh vÏ:
X
2
X
1
α
TRÇN QUANG THANH-K15-CAO HäC Lý -§H VINH
2
gãc
α
= gãc(HOM)
Ta tÝnh
α
qua c«ng thøc
A
X
OM
HM
1
sin ==
α
(Chó ý : ®−êng trßn cã b¸n kÝnh b»ng biªn ®é A )
ω
+
NÕu bµi tËp cho gi¸ trÞ x
1
cô thÓ th× ta suy ra ngay A
gãc
α
vµ tõ ®ã suy ra thêi gian cÇn tÝnh M
ω
α
=
min
t
víi
α
tÝnh theo rad
(VD:
α
=60
O
th× lÊy lµ b»ng
3
π
)
-A
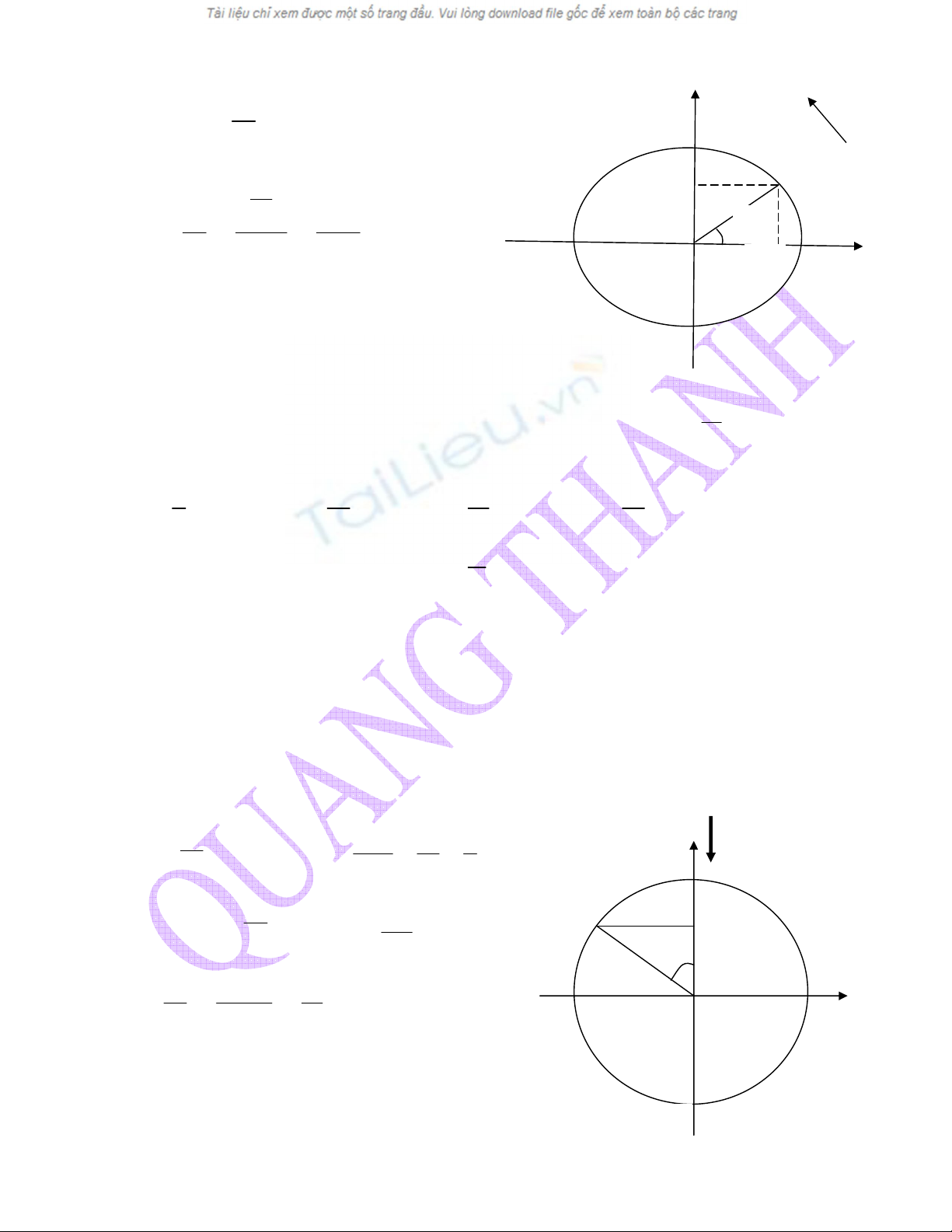
TH2: VËt ®i tõ vÞ trÝ x
1
(d−¬ng) ®Õn vÞ trÝ biªn ®é A
th× gãc quÐt lóc nµy t−¬ng øng trªn h×nh vÏ lµ
α
A +
víi
α
=gãc(HOM). Ta dïng c«ng thøc:
M
A
X
OM
OH
1
cos ==
α
T−¬ng tù suy ra gãc
α
vµ thêI gian
ω
α
=
min
t
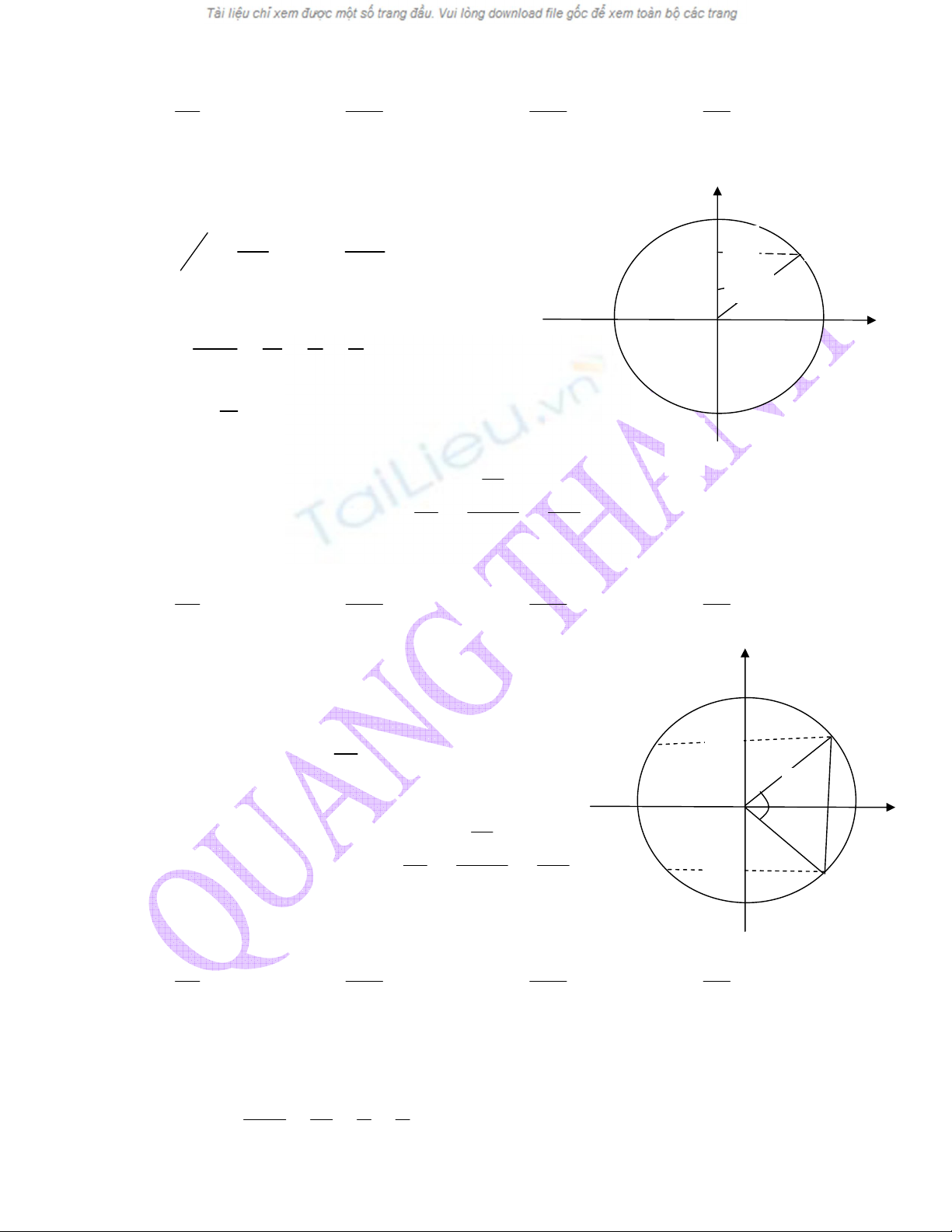
TH 3: VËt ®i tõ vÞ trÝ x
1
®Õn vÞ trÝ x
2
nh− h×nh vÏ bªn
th× th−êng gãc
α
sÏ ®¬n gi¶n h¬n. NÕu tam gi¸c
OMN ®Òu th× gãc
α
= 60
0
lóc nµy chØ cÇn thay
vµo c«ng thóc
lµ xong:
ω
α
=
min
t
TH 4 : Lµ tr−êng hîp phøc t¹p h¬n tïy vµo bµi
ra mµ ta cã thÓ vÏ b»ng ph−¬ng ph¸p trªn t«i se tr×nh bµy trong bµi tËp cô thÓ
PHÇN BµI TËP
BµI 1: mét vËt dao ®éng ®iÒu hßa víi biªn ®é A= 4(cm) vµ chu kú dao ®éng T=0,1(s).
VËt ®i qua VTCB theo chiÒu d−¬ng .
1.TÝnh kho¶ng thêi gian ng¾n nhÊt ®Ó vËt ®i tõ vÞ trÝ cã li ®é X
1
=2(cm) ®Õn X
2
=4(cm) .
X
1
H
α
O
X
1
H
α
-
A
TRÇN QUANG THANH-K15-CAO HäC Lý -§H VINH
3
A.
)(
10
1st =
B.
)(
100
1st =
C.
)(
120
1st =
D.
)(
60
1st =
Bµi gi¶i: Khi vËt chuyÓ ®éng trªn trôc ox tõ vÞ trÝ 2(cm) ®Õn 4(cm) th× t−¬ng øng trªn
vßng trßn vËt M ®Õn Q víi gãc quÐt
α
=gãc ( HOM)
Ta cã A= 4(cm): T=0,1(S) Suy ra
)(20
1,0
2
2
s
rad
T
π
π
π
ω
===
Cßn gãc
α
tÝnh theo c«ng thøc :
2
1
4
22
cos ====
A
OM
OH
α
Suy ra
)(
3
rad
π
α
=
vËy thêi gian cÇn tÝnh lµ :
)(
60
1
20
3
min
st ===
π
π
ω
α
2. TÝnh kho¶ng thêi gian ng¾n nhÊt ®Ó vËt ®i tõ vÞ trÝ X
1
=-2(cm) ®Õn vÞ trÝ X
2
=2(cm)
A.
)(
10
1st =
B.
)(
100
1st =
C.
)(
120
1st =
D.
)(
60
1st =
Bµi gi¶i: T−¬ng tù nh− trªn lóc nµy vËt quÐt ®−îc
mét gãc
α
= gãc(MON)
Do OM=ON=MN= A=4(cm) nªn tam gi¸c
OMN ®Òu. Suy ra
3
π
α
=
VËy thêI gian cÇn t×m lµ
)(
60
1
20
3
min
st ===
π
π
ω
α
3. TÝnh thêi gian ng¾n nhÊt ®Ó vËt ®i tõ VTCB O
®Õn vÞ trÝ cã li ®é X=2(cm)
A.
)(
10
1st =
B.
)(
100
1st =
C.
)(
120
1st =
D.
)(
60
1st =
Bµi gi¶i : T−¬ng tù 2 c©u trªn khi vËt ®i tõ VTCB O
®Õn vÞ trÝ x=2(cm) t−¬ng øng vËt quÐt ®−îc gãc
α
= gãc(MOH)
Ta cã
2
1
4
2
sin ====
A
X
OM
HM
α
Q
M
O
2
4
-
4
H
α
4
-
4
2
-
2
O
N
M
α
TRÇN QUANG THANH-K15-CAO HäC Lý -§H VINH
4
Suy ra
6
π
α
=
VËy thêi gian cÇn t×m lµ :
)(
120
1
20
6
min
st ===
π
π
ω
α
BµI 2: VËt dao ®éng ®iÒu hßa víi ph−¬ng tr×nh :
))(
2
2sin(10 cmtx
π
π
+=
.T×m thêi
®iÓm vËt qua vÞ trÝ cã li ®é X=5(cm) lÇn thø hai theo chiÒu d−¬ng?
A.
)(
6
1st =
B.
)(
16
1st =
C.
)(
6
11 st =
D.
)(
6
15 st =
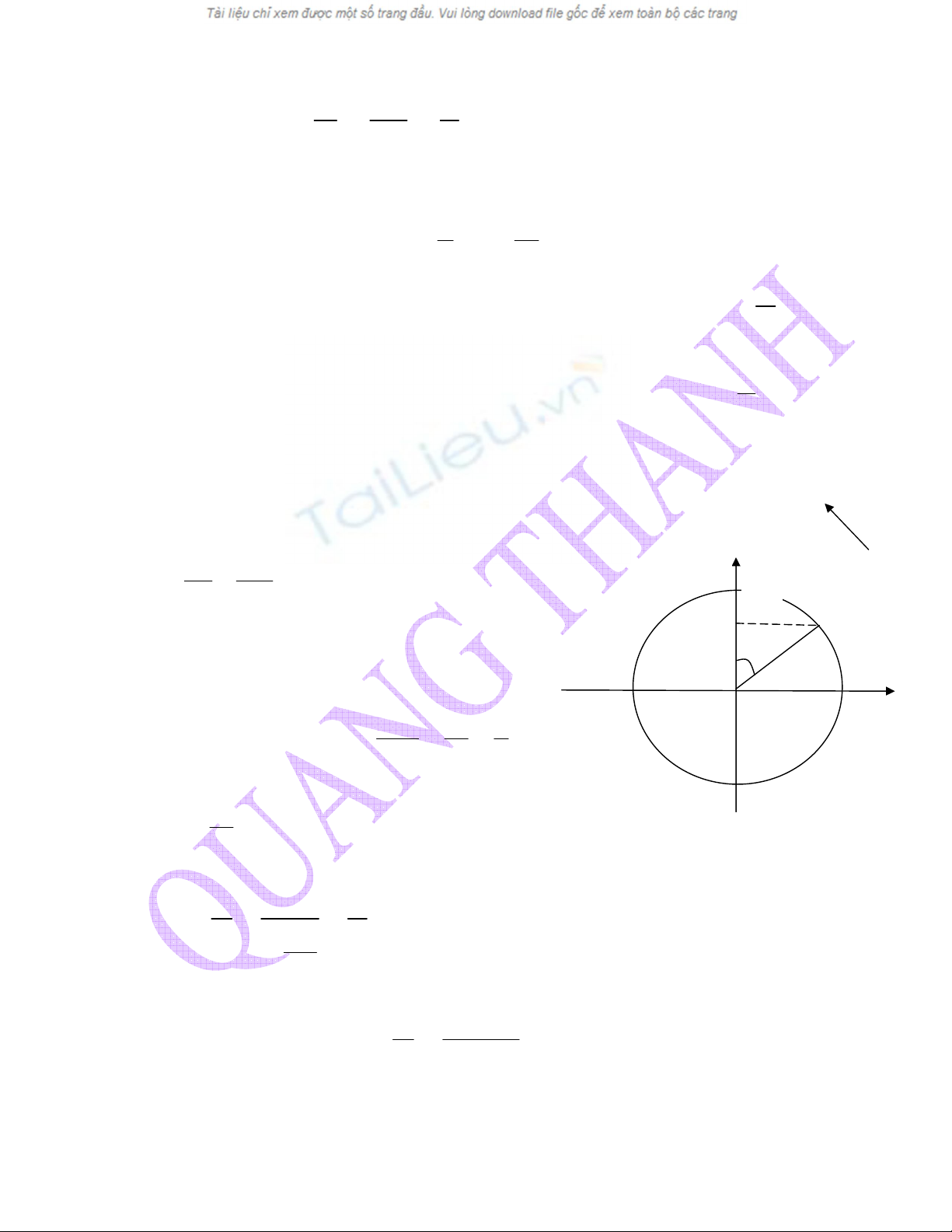
Bµi gi¶i: nhËn xÐt : do pha ban ®Çu
2
π
ϕ
=
nªn t¹i thêi ®iÓm ban ®Çu t=0 vËt b¾t ®Çu
dao ®éng tõ vÞ trÝ biªn d−¬ng ( quay l¹i VTCB) ( trªn h×nh vÏ lµ ®i tõ A vÒ O) . Ta cã
c«ng thøc tÝnh thêi gian vËt ®i qua vÞ trÝ x=5(cm) lÇn thø nhÊt theo chiÒu d−¬ng lµ :
o
tTt −=
1
(víi t
o
lµ kho¶ng thêi gian ng¾n nhÊt ®Ó vËt ®i tõ vÞ trÝ biªn d−¬ng dÕn vÞ trÝ cã li ®é
x=5(cm) , T lµ chu kú )
ViÖc tÝnh t
0
dùa vµo ®−êng trßn l−îng gi¸c nh− sau : khi vËt dao ®éng tõ A vÒ P th× vËt
chuyÓn ®éng trßn ®Òu tõ A ®Õn M . Kho¶ng thêi gian ng¾n nhÊt t
0
®Ó vËt ®i trªn qu·ng
®−êng nµy lµ :
ω
α
=
0
t
víi
2
1
10
5
cos ===
OM
OP
α
Suy ra :
3
π
α
=
vµ
T
π
ω
2
=
nªn
6
2
.
3
.
0
TT
t===
π
π
ω
α
vËy thêi ®iÓm
vËt ®i qua vÞ trÝ cã li ®é x=5(cm) theo
chiÒu d−¬ng lÇn thø nhÊt lµ
4
-
4
O
H
M
2
α
H
O
2
α
A
M
P
O
-
A
TRÇN QUANG THANH-K15-CAO HäC Lý -§H VINH
5
)(
6
5
6
5
6
1
S
TT
TtTt
o
==−=−=
Do T= 1(S) . KÕt luËn thêi gian vËt ®i qua vÞ trÝ cã li ®é x=5(cm) theo chiÒu d−¬ng lÇn
thø 2 lµ :
)(
6
11
1
6
5
12
STtt =+=+=
Bµi 3: Mét vËt dao ®éng ®iÒu hßa theo ph−¬ng tr×nh:
))(
2
10sin(10 cmtx
π
π
+=
X¸c ®Þnh thêi ®iÓm vËt ®i qua vÞ trÝ cã li ®é x=5(cm) lÇn thø 2002?
Bµi gi¶i: V× vËt b¾t dao ®éng t¹i vÞ trÝ biªn d−¬ng( do t=o th×
2
sin10
π
=x
=10 > 0 ) vµ
trong mçi chu kú vËt qua vÞ trÝ x=5(cm0 hai lÇn . Cho nªn vËt qua vÞ trÝ x=5(cm) 2002lÇn
th× vËt ph¶i thùc hiÖn ®−îc 1001 chu kú dao ®éng . VËy thêi ®iÓm vËt qua vÞ trÝ x=5(cm)
lÇn thø 2002 x¸c ®Þnh theo hÖ thøc :
1
1001 tTt
−
=
+
víi
)(2,0
10
22 ST ===
π
π
ω
π
cßn t
1
lµ kho¶ng thêi gian
ng¾n nhÊt ®Ó vËt ®i tõ vÞ trÝ x=5(cm0 ®Õn vÞ trÝ
biªn d−¬ng (x=10cm . Dôa vµo h×nh vÏ ta tÝnh
thêi gian t
1
nh− sau :
2
1
10
5
cos ===
OM
OP
α
Nªn
3
π
α
=
VËy 6
2
.3
1
T
T
t===
π
π
ω
α
Suy ra thêi gian cÇn t×m lµ
)(17,200
6
6005
6
.10011001
1
S
TT
TtTt ==−=−=
10
-
10
5
0
M
P


























