250
PHƯƠNG PHÁP LÝ THUYẾT NHIỄU LOẠN
GIẢI BÀI TOÁN NGUYÊN TỬ HYDRO TRONG TỪ TRƯỜNG ĐỀU
Nguyễn Phương Duy Anh1
1. Viện Phát Trin Ứng Dụng, Trường Đại học Thủ Dầu Một
TÓM TẮT
Các bài toán chuyn động trong thế giới vi mô được mô tả bới phương trình Schrödinger,
một phương trình đạo hàm riêng tuyến tính phức tạp, chỉ có th giải chính xác trong một số
trường hợp đơn giản. Trong công trình này chúng tôi sử dụng lý thuyết nhiễu loạn đ giải
phương trình Schrödinger cho bài toán nguyên tử hydro trong từ trường đều, phương pháp này
đã được giới thiệu trong các sách giáo khoa về Cơ học lượng tử. Thông qua sơ đồ lý thuyết
nhiễu loạn Rayleigh-Schrödinger, chúng tôi đã thu được kết quả số với độ chính xác cao, đến
4 chữ số thập phân. Các kết quả thu được hoàn toàn trùng khớp với các kết quả của các công
trình khác (Rosner 1984; Thirumalai 2009). Qua phân tích kết quả chúng tôi nhận thấy phương
pháp lý thuyết nhiễu loạn cho kết quả tốt trong vùng từ trường yếu, với cường độ
0.4
(từ
trường không thứ nguyên), còn trong vùng từ trường mạnh thì không còn đúng nữa. Nguyên
nhân của vấn đề này đó là do khi từ trường biến đổi trong vùng từ trường mạnh
0.4
thì
thành phần tách ra không đủ nhỏ đ coi là “nhiễu loạn”, vì vậy trong công trình tiếp theo chúng
tôi tiếp tục phát trin phương pháp lý thuyết nhiễu loạn nhằm khắc phục những hạn chế khi
tính toán trong vùng từ trường có giá trị lớn.
Từ khóa: lý thuyết nhiễu loạn, nguyên tử hydro, từ trường đều
1. MỞ ĐẦU
Như chúng ta đã biết, tất cả các bài toán chuyển động trong thế giới vi mô đều dẫn đến việc
giải phương trình Schrödinger. Đây là một phương trình đạo hàm riêng tuyến tính phức tạp mà
nghiệm chính xác của nó chỉ có thể xác định được trong một số trường hợp đơn giản với thế năng
đã được lý tưởng hóa (nguyên tử hydro, bài toán dao động tử đều hòa, chuyển động trong hố thế
vuông góc...). Do đó, đối với các bài toán liên quan đến hệ lượng tử thực, người ta phải dùng các
phương pháp tính gần đúng để tìm hàm riêng, trị riêng của nó. Phương pháp nhiễu loạn là một
trong những phương pháp tính gần đúng rất quan trọng của Cơ lượng tử, tính hiệu quả của nó đã
được kiểm chứng nhiều năm (Đặng Quang Khang 2006; Hoàng Dũng 1999). Bên cạnh những ưu
điểm thì phương pháp này cũng bộc lộ một số hạn chế như tính hội tụ của chuỗi nhiễu loạn và
miền ứng dụng của phương pháp này. Trong công trình này chúng tôi sẽ sử dụng lý thuyết nhiễu
loạn để giải bài toán nguyên tử hydro trong từ trường đều, là một trong số các bài toán có thể giải
được nghiệm số chính xác (Rosner 1984; Thirumalai 2009), dùng kết quả số thu được so sánh với
các công trình (Rosner 1984; Thirumalai 2009) để tìm được vùng làm việc hiệu quả của phương
pháp lý thuyế nhiễu loạn. Có nhiều sơ đồ lý thuyết nhiễu loạn khác nhau nhưng về cơ bản nó chỉ
thay đổi tốc độ hội tụ một ít chứ không giải quyết được vấn đề mở rộng miền sử dụng, trong phần
này chúng tôi trình bày sơ đồ Rayleigh- Schrödinger là sơ đồ thông dụng nhất, được trình bày
trong phần lớn sách giáo khoa về cơ học lượng tử (Đặng Quang Khang 2006; Hoàng Dũng 1999).
Sơ đồ này cũng sẽ được sử dụng để giải bài toán nguyên tử hydro trong từ trường đều.
251
2. SƠ ĐỒ RAYLEIGH- SCHRÖDINGER CHO PHƯƠNG PHÁP NHIỄU LOẠN DỪNG
Xét phương trình Schrödinger dừng:
ˆ( ) ( ).H x E x =
(1)
Giả sử ta có thể tách toán tử Hamiltonian của bài toán thành hai thành phần như sau:
0
ˆ ˆ ˆ,H H V
=+
(2)
trong đó thành phần
0
ˆ
H
là toán tử Hamiltonian có nghiệm riêng chính xác
0
ˆ,
n n n
H
=
(3)
thành phần
ˆ
V
còn lại gọi là thế nhiễu loạn. Điều kiện áp dụng lý thuyết nhiễu loạn là thành
phần nhiễu loạn
ˆ
V
phải “nhỏ” so với
0
ˆ
H
:
0
ˆˆ
VH
. Ở đây ta đưa vào tham số nhiễu loạn
để coi thành phần nhiễu loạn là nhỏ và dễ dàng nhìn thấy các bậc nhiễu loạn trong sơ đồ tính
toán giải tích qua các số mũ của
, trong kết quả cuối cùng khi tính số ta có thể cho
1
=
.
Khi đó nghiệm của phương trình (3) sẽ gần với nghiệm của phương trình (1) còn nghiệm với
gần đúng bậc cao sẽ được tính bằng cách xét đến ảnh hưởng của
ˆ
V
thông qua các bổ chính
năng lượng và hàm sóng.
Ta giả thuyết rằng các trị riêng của
ˆ
H
là không suy biến và có phổ gián đoạn, hệ hàm
riêng
n
của
0
ˆ
H
là đầy đủ và trực giao ứng với năng lượng
n
, với
0,1,2...n=
. Khi đó, ta
tìm nghiệm của (1) dưới dạng khai triển các hàm riêng của
0
ˆ
H
như sau:
( ) ( )
0
.
kk
k
x C x
+
=
=
(4)
Không mất tính tổng quát ta có thể giả thuyết hàm sóng cho trạng thái n như sau:
( ) ( ) ( )
( )
0
.
n n k k
k k n
x x C x

+
=
= +
(5)
Thay (5) vào (1) ta được:
( )
( ) ( )
( )
( ) ( )
( )
0
00
ˆˆ .
n k k n n k k
k k n k k n
H V x C x E x C x
+ +
= =
+ + = +

(6)
Nhân hai vế (6) với
( )
*
nx
rồi tích phân theo toàn miền biến số x ta được:
( )
0
.
nn nn k nk n
k k n
H V C V E

+
=
+ + =
(7)
Làm tương tự như trên cho
( ) ( )
*,
jx j n
ta được:
( )
( )
( )
0
,,
n jj j jn k jk
k k n
E H C V C V j n

+
=
− = +
(8)
với ký hiệu các yếu tố ma trận:
252
( ) ( ) ( ) ( )
*
0
ˆˆ
,.
kk k k jk j k
H x H x dx V x V x dx
+ +
− −
==

(9)
Hệ phương trình đại số (7), (8) có thể xem tương đương với phương trình Schrödinger
(1). Giải hệ phương trình này ta thu được năng lượng
n
E
và các hệ số
j
C
, nghĩa là tìm được
hàm sóng
( )
nx
qua công thức (5). Ta có thể sử dụng lý thuyết nhiễu loạn cho hệ phương
trình này bằng cách phân tích theo tham số nhiễu loạn như sau:
( ) ( )
0
1
,
s
s
nn
s
E E E
+
=
= +
(10)
( ) ( )
0
1
,.
s
s
j j j
s
C C C j n
+
=
= +
(11)
Ở đây ta kí hiệu
( ) ( )
00
,
nj
EC
là năng lượng và hệ số gần đúng bậc không, còn
( )
s
E
,
( )
s
j
C
là các bổ chính vào năng lượng và hệ số hàm sóng. Thay (10) và (11) vào (7) và (8) sau đó đồng
nhất hai vế theo lũy thừa của tham số
ta được:
( ) ( ) ( ) ( ) ( )
( )
0 0 1 1
0
, 0, , .
jn
n nn j n nn j
n jj
V
E H C E V C j n
EH
= = = =
−
(12)
Khi
2s
:
( ) ( )
( )
1
0
,
ss
n nk k
k k n
E V C
+ −
=
=
(13)
( ) ( ) ( )
( )
( ) ( )
( )
1
1
0
01
1,.
s
s s s t t
j jk k n j
k k n t
n jj
C V C E C j n
EH
+ −
−−
= =

= −


−

(14)
Đây là sơ đồ lý thuyết nhiễu loạn mà chúng ta sẽ sử dụng trong các phần sau.
3. ỨNG DỤNG CHO BÀI TOÁN NGUYÊN TỬ HYDRO TRONG TỪ TRƯỜNG
Trước tiên ta xây dựng phương trình Schrodinger cho nguyên tử hydro trong từ trường
đều. Nghĩa là ngoài tương tác Coulomb, electron còn chuyển động dưới tác dụng của từ trường
đều. Với điều kiện định chuẩn Lorentz
.0A=
, Hamiltonian có dạng:
22
22
2
0
1ˆˆ
ˆ..
24
2
e e Ze
H p A p A
m mc r
mc

= + + −
(15)
Trong đó thế vectơ
A
có thể chọn dưới dạng thuận lợi sau:
1,
2
A r B= −
(16)
với
B
là véc-tơ từ trường. Không mất tính tổng quát, ta cho véc-tơ từ trường hướng theo phương
trục z. Khi đó Hamiltonian (15) có dạng:
253
( )
2 2 2
2 2 2
2
0
1 1 1
ˆ
ˆˆ ,
2 2 8 4
z
e e B e Z
H r p BL x y
m mc r
mc


= + + + −

(17)
với
ˆz
L
là toán tử hình chiếu mô-men quỹ đạo trên trục Oz.
Bây giờ ta có thể viết phương trình Schrodinger cho nguyên tử hydro chuyển động trong
từ trường như sau:
( ) ( )
ˆ, , , , ,H x y z x y z

=
(18)
với
( )
2 2 2
2 2 2
2 2 2 2 2 2
1 1 1
ˆ.
2 2 8
z
Z
H L x y
x y z x y z


= − + + + + + −

++

(19)
Ở đây ta đã đưa phương trình về dạng không thứ nguyên, được trình bày như trong phụ
lục, trong đó đơn vị độ dài là bán kính Borh:
2
0
2
4
ame

=
, đơn vị năng lượng là 2 lần hằng số
Rydberg:
4
22
0
8
y
me
Rh
=
, từ trường không thứ nguyên
được xác định bằng biểu thức
2y
mcR
Be
=
.
Để đánh giá độ lớn tương đối của từ trường so với tương tác Coulomb, ta đưa ra phép so
sánh sau: thang năng lượng từ trường được đặc trưng bởi giá trị
c
eB
mc
=
(Nguyen 2019),
trong khi thang năng lượng tương tác Coulomb được đặc trưng bởi hằng số Rydberg
y
R
. Như
vậy hệ số so sánh giữa hai thang năng lượng là
2
c
y
R
=
. Từ đây ta có thể gọi từ trường yếu
ứng với giá trị
1

và từ trường mạnh ứng với giá trị
1

.
Ta sẽ giải phương trình (18) cho trạng thái cơ bản bằng phương pháp nhiễu loạn. Ta tách
toán tử Hamilton (19) làm hai phần:
2 2 2
02 2 2 2 2 2
11
ˆ
2
Hx y z x y z

= − + + −

++

(20)
và
( )
2 2 2
1
ˆ.
8
V x y
=+
(21)
Ở đây với trường hợp trạng thái cơ bản
0
z
L=
, ta xét trường hợp nguyên tử hydro:
1Z=
. Cách tách này hoàn toàn phù hợp với lý thuyết nhiễu loạn là
0
ˆ
H
có nghiệm riêng chính xác
là hàm sóng của electron ở trạng thái cơ bản của nguyên tử hydro
( )
0
1,
r
re
−
=
(22)
254
và ứng với trị riêng là năng lượng gần đúng bậc zero
00.5
=−
.
Năng lượng gần đúng đến bổ chính bậc một có dạng:
( )
( ) ( ) ( ) ( )
2
1*
0 0 0 0
ˆˆ
.
4
r V r r V r dV
= = =
(23)
Khi đó ta có:
( ) ( )
11 2
00 0.5 0.25 ,
= + = − +
(24)
với giá trị cụ thể ghi trong bảng 1. Trong bảng 1, để tiện so sánh với các kết quả của các công
trình khác, ta chuyển sang năng lượng liên kết được tính bằng công thức
1
2,
2
lk

=−


(25)
với đơn vị là hằng số Rydberg.
( )
1
0
0
liên kết
Tài liệu (Rosner 1984)
Tài liệu (Thirumalai 2009)
0
-0.5
1
-
-
0.01
-0.499975
1.00995
1.009950
-
0.02
-0.4999
1.0198
1.019800
1.0198
0.04
-0.4996
1.0392
1.039201
1.0392
0.1
-0.4975
1.095
1.095053
1.0951
0.2
-0.49
1.18
1.180763
1.1808
0.4
-0.46
1.32
1.329211
1.3293
1
-0.25
1.5
1.662338
1.6624
2
0.5
1
2.044428
2.0445
4
3.5
3
2.561596
2.5616
10
24.5
39
3.495594
3.4956
20
99.5
179
4.430797
4.4308
40
399.5
759
5.602058
-
100
2499.5
4899
7.5781
-
Bảng 1: Năng lượng trạng thái cơ bản tính đến bổ chính bậc 1
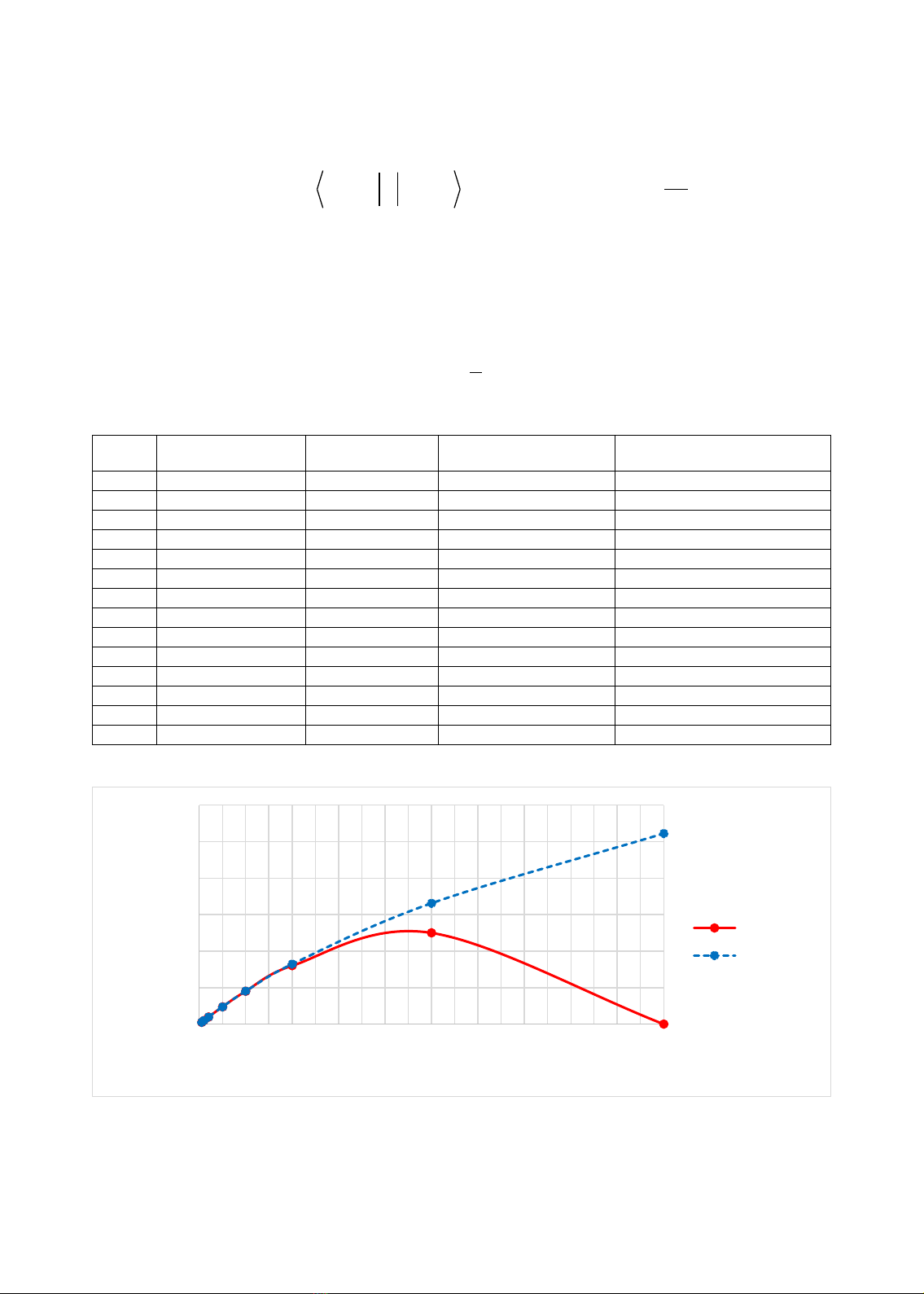
Hình 1: Năng lượng liên kết ở trạng thái cơ bản thu được bằng phương pháp lý thuyết nhiễu
loạn đến bổ chính bậc 1 (đường liền nét màu đỏ) so sánh với kết quả của của công trình khác
(Rosner 1984) (đường đứt nét màu xanh)
1,00000
1,20000
1,40000
1,60000
1,80000
2,00000
2,20000
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2
Năng lượng liên kết
Từ trường γ
LTNL
Rosner 1984