
Lyù thuyeát qui hoaïch tuyeán tính
C H NG VI: T I U TUY N TÍNH CH A THAM SƯƠ Ố Ư Ế Ứ Ố
Trong th c t , m t s mô hình bài toán t i tuy n tính, các h s ban đ u nh aự ế ở ộ ố ố ế ệ ố ầ ư ij, bi,
cj, i = 1,2,…,m; j = 1,2,…,n, có th không đ c cho bi t m t cách chính xác ho c giá trể ượ ế ộ ặ ị
c a chúng th ng ph thu c vào s thay đ i c a m t hay nhi u tham s nh th i gian,ủ ườ ụ ộ ự ổ ủ ộ ề ố ư ờ
th i ti t, ch t l ng nguyên li u, nhiên li u v.v… N u ph i ti n hành vi c gi i bài toánờ ế ấ ượ ệ ệ ế ả ế ệ ả
ng v i t ng giá tr khác nhau c a các tham s y thì kh i l ng và do đóchi phí tính toánứ ớ ừ ị ủ ố ấ ố ượ
s r t l n và, do v y, vi c gi i bài toán T TT tìm ph ng án t i u s m t h t ý nghĩaẽ ấ ớ ậ ệ ả Ư ươ ố ư ẽ ấ ế
kinh t .ế
Đ kh c ph c khó khăn này ng i ta đã phát tri n m t ph ng pháp g i là ể ắ ụ ườ ể ộ ươ ọ ph ngươ
pháp gi i bài toán T TT ch a tham. ả Ư ứ Ph ng pháp này xu t phát t vi c gi i bài toánươ ấ ừ ệ ả
T TT đ i v i m t giá tr xác đ nh c a tham s c n kh o sát b ng ph ng pháp đ n hìnhƯ ố ớ ộ ị ị ủ ố ầ ả ằ ươ ơ
thông th ng, Sau đó s tìm kho ng bi n thiên c a tham s đ cho ph ng án hi n cóườ ẽ ả ế ủ ố ể ươ ệ
v n còn là ph ng án t i u c a bài toán m i ho c s tr c ti p tìm ra ph ng án t i uẫ ươ ố ư ủ ớ ặ ẽ ự ế ươ ố ư
m i d a trên ph ng án t i u hi n có. B ng cách y ng i ta s tìm ra ph ng án t i uớ ự ươ ố ư ệ ằ ấ ườ ẽ ươ ố ư
c a các bài toán T TT ng v i t ng giá tr khác nhau c a tham s c n kh o sát. ủ Ư ứ ớ ừ ị ủ ố ầ ả
Ng i ta phân bi t thành bài toán qui ho ch tuy n tính ch a m t tham s h s hàmườ ệ ạ ế ứ ộ ố ở ệ ố
m c tiêu (cụj), v ph i (bở ế ả i), h s các ràng bu c (aở ệ ố ộ ij), ch a m t tham s c hàm m cứ ộ ố ở ả ụ
tiêu và v ph i ho c ch a hai tham s cùng bi n thiên đ c l p v.v….Trong ph m vi giáoở ế ả ặ ứ ố ế ộ ậ ạ
trình này chúng tôi ch xét hai lo i bài toán đ u tiên. ỉ ạ ầ
T ng t nh các ch ng tr c chúng tôi không đi sâu vào phân tích c s lý thuy tươ ự ư ở ươ ướ ơ ở ế
c a ph ng pháp gi i, không trình bày k ph n ch ng minh các đ nh lý mà chú tr ng trìnhủ ươ ả ỹ ầ ứ ị ọ
bày thu t toán gi i và các ý nghĩa kinh t cũng nh th c ti n. Đ nghiên c u thêm ph n cậ ả ế ư ự ễ ể ứ ầ ơ
s lý thuy t, tìm hi u thêm các ph ng pháp gi i bài toán T TT ch a tham s khác, b nở ế ể ươ ả Ư ứ ố ạ
đ c có th tham kh o thêm [ ].ọ ể ả ở
2.1 Ph ng pháp đ n hình gi i bài toán T TT ch a tham s hàm m c tiêuươ ơ ả Ư ứ ố ở ụ
2.1.1. C s lý thuy t và thu t toánơ ở ế ậ
Ta xét bài toán qui ho ch sau đây: ạ
Tìm giá tr c a xị ủ 1, x2,…, xn làm c c ti u hàm m c tiêuự ể ụ
∑+= =
n
1j jjj x)tdc()x(Z
(2.1)
ng v i các ràng bu cứ ớ ộ
( )
1
, 1,2,..., (2.2)
0, 1,2,..., 2.3
n
ij j i
j
j
a x b i m
x j n
== =
≥ =
∑
u ≤ t ≤ v (2.4)
Trong đó cj, dj, aij, bi, i = 1,2,…,m; j = 1,2,…,n và u, v là các s cho tr c; ố ướ t là tham s ; u cóố
th là -ể∞, v có th là + ể∞; t c tham s t có th không b ch n d i ho c không b ch nứ ố ể ị ặ ướ ặ ị ặ
trên.
Đ th y r ng ng v i m i giá tr c đ nh c a tham s t = tễ ấ ằ ứ ớ ỗ ị ố ị ủ ố 0∈[u,v] bài toán t i uố ư
ch atham s (2.1) – (3.3) tr thành bài toán T TT bình th ng. Vì v y, ng i ta g i bàiứ ố ở Ư ườ ậ ườ ọ
toán (2.1) - (2.4) là bài toán T TT ch a tham s (hay, ng n g n, Ư ứ ố ắ ọ bài toán t i u tham số ư ố).
Ngoài ra, đ cho bài toán tham s có ý nghĩa thì ngoài các gi thi t c n có c a bài toánể ố ả ế ầ ủ
Lê V n Phiă87

Lyù t huyeát qui hoaï ch t uyeán tí nh
T TT thông th ng ng i ta còn gi thi t r ng ít nh t m t h s dƯ ườ ườ ả ế ằ ấ ộ ệ ố j, 1 ≤ j ≤ n, là khác
không, b i vì, n u dở ế j = 0, ∀j, thì bài toán (2.1)-(2.4) tr thành bài toán T TT thông th ng. ở Ư ườ
Nh m đ n gi n cách trình bày b t đ u t đây chúng ta ký hi u bài toán (2.1)-(2.4) làằ ơ ả ắ ầ ừ ệ
P(0, t). Ta nh n th y r ng các aậ ấ ằ ij và bi, i = 1,2,…,m; j = 1,2,…, n, đ u không ph thu c vàoề ụ ộ
tham s t nên t p các ph ng án ch p nh n đ c X là nh nhau ng v i m i giá tr c a t.ố ậ ươ ấ ậ ượ ư ứ ớ ọ ị ủ
Vì v y, n u ng v i m t giá tr nào đó c a tham s t mà mi n ch p nh n đ c r ng thìậ ế ứ ớ ộ ị ủ ố ề ấ ậ ượ ỗ
hi n nhiên mi n ch p nh n đ c c a bài toán (2.1) – (2.4) cũng là r ng v i m i giá tr c aể ề ấ ậ ượ ủ ỗ ớ ọ ị ủ
t. Trong tr ng h p này bài toán t i u tuy n tính tham s (2.1) – (2.4) không gi i đ cườ ợ ố ư ế ố ả ượ
v i m i giá tr c a t, đ c bi t v i tớ ọ ị ủ ặ ệ ớ ∈[u,v].
Ph ng pháp gi i bài toán t i u tham s (2.1) - (2.4) b t đ u b ng vi c cho tham s tươ ả ố ư ố ắ ầ ằ ệ ố
nh n giá tr tậ ị 0 nào đó thu c [u,v] (n u u là h u h n, ta đ t t = u)ộ ế ữ ạ ặ 26. Sau đó áp d ng ph ngụ ươ
pháp đ n hình (ho c đ n hình m r ng) gi i bài toán P(0,tơ ặ ơ ở ộ ả 0). Đ d dàng cho vi c th cể ễ ệ ự
hi n ph ng pháp gi i v sau các h s đ c tr ng aệ ươ ả ề ệ ố ặ ư m+1,j đ c tính tách riêng theo các hượ ệ
s cốj và dj t ng ng d i d ng: aươ ứ ướ ạ m+1,j = h j + gjt ,j = 0,1,2,…,n (trong đó hj đ c tính theo cượ j
và gj theo dj). Có 3 tr ng h p x y ra:ườ ợ ả
•Tr ng h p 1ườ ợ : Bài toán P(0,t0) không có l i gi i ch p nh n đ c. ờ ả ấ ậ ượ
•Tr ng h p 2ườ ợ : Bài toán P(0,t0) không có l i gi i t i u; t c là hàm m c tiêu (2.1) ngờ ả ố ư ứ ụ ứ
v i t = tớ0 không b ch n d i trên t p h p ch p nh n đ c.ị ặ ướ ậ ợ ấ ậ ượ
•Tr ng h p 3ườ ợ : Bài toán P(0,t0) có l i gi i c s t i u là xờ ả ơ ở ố ư 0.
Ta l n l t xét các tr ng h p 1, 2 và 3.ầ ượ ườ ợ
1) Xét tr ng h p 1ườ ợ :
Vì nh nh n xét trên, t p ch p nh n đ c c a bài toán P(0,t) là nh nhau đ i v iư ậ ở ậ ấ ậ ượ ủ ư ố ớ
m i giá tr c a t nên, n u t p này là r ng ng v i m t giá tr t = tọ ị ủ ế ậ ỗ ứ ớ ộ ị 0 nào đó, thì nó cũng là t pậ
r ng ng v i m i giá tr c a t. T c là bài toán t ng quát P(0,t) không có l i gi i ch p nh nỗ ứ ớ ọ ị ủ ứ ổ ờ ả ấ ậ
đ c ng v i m i giá tr t.ượ ứ ớ ọ ị
2) Xét tr ng h p 2ườ ợ :
Không làm m t tính t ng quát và đ đ n gi n cách trình bày, gi s ph ng pháp đ nấ ổ ể ơ ả ả ử ươ ơ
hình gi i bài toán P(0,tả0) d ng l i b ng đ n hình ng v i ph ng án c b n ừ ạ ở ả ơ ứ ớ ươ ơ ả x0 có d ngạ
chính t c m r ng nh sau:ắ ở ộ ư
1
n
i ij j i
j m
x a x b
= +
+ =
∑
, i = 1,2,…,m
1, 0 1 0
1
( ) ( )
n
m j j m
j m
Z a t x b t
+ +
= +
+ =
∑
(2.5)
Giá tr các bi n c s xị ế ơ ở 0i = ai0 ≥ 0, i =1,2,…,m, và giá tr các bi n phi c s xị ế ơ ở j j = m+1, 2, . .
., n, đ u b ng 0; t c là xề ằ ứ m+k = 0. Đ ng th i giá tr hàm m c tiêu t ng ng Zồ ờ ị ụ ươ ứ 0 = bm+1. Theo
qui c nh trên các các h s đ c tr ng aướ ư ệ ố ặ ư m+1,j có d ngạ
am+1,j (t) = h j + g j.t, j = 0, 1,2,…,n (2.6)
Trong đó
1 1
, , 1,2,...
m m
j ij Bi j j ij Bi j
i i
h a c c g a d d j n
= =
= − = − =
∑ ∑
(2.7)
26 Trên th c t , ng i ta th ng ch n t = tự ế ườ ườ ọ 0 sao cho d dàng áp d ng ph ng pháp đ n hình tìm l i gi i t i u c aễ ụ ươ ơ ờ ả ố ư ủ
bài toán P(0,t0).
Lê V n Phiă88

Lyù thuyeát qui hoaïch tuyeán tính
0 0
1 1
,
m m
i i i i
i i
h cb g d b
= =
= =
∑ ∑
(2.8)
Giá tr hàm m c tiêu ng v i ph ng án c s ị ụ ứ ớ ươ ơ ở x0 là
bm+1 (t0) = h 0 + g 0.t0, (2.9)
Theo thu t toán đ n hình, tr ng h p 2 x y ra khi t n t i m t h s đ c tr ng aậ ơ ườ ợ ả ồ ạ ộ ệ ố ặ ư m+1,l =
hl, + gl.t0 > 0, m+1≤ l ≤ n, và yi,l ≤ 0, i =1,2,…, m và do đó hàm m c tiêu s không b ch nụ ẽ ị ặ
d i trên t p các ph ng án ch p nh n đ c c a bài toán ng v i t = tướ ậ ươ ấ ậ ượ ủ ứ ớ 0. T đó ta xét 3ừ
tr ng h p con nh sau:ườ ợ ư
i) gl = 0: Khi đó hàm m c tiêu c a bài toán P(0,t) không b ch n d i ng v i m i giáụ ủ ị ặ ướ ứ ớ ọ
tr c a t, vì ị ủ
am+1,l (t) = hl, + gl.t = hl > 0, ∀t.
K t h p v i đi u ki n aế ợ ớ ề ệ i,l ≤ 0, i =1,2,…, m, suy ra bài toán không gi i đ c ả ượ ∀t.
ii) gl > 0: Khi đó am+1,l (t) = hl, + gl.t > 0 ng v i m i giá tr c a t > t’, v i ứ ớ ọ ị ủ ớ
0
l
lt
g
h
't <−=
(2.10)
Suy ra ∀t > t’ bài toán P(0,t) có hàm m c tiêu không b ch n d i và, do đó, khôngụ ị ặ ướ
gi i đ c. N u t’< u, thì bài toán P(0,t) không gi i đ c v i m i tả ượ ế ả ượ ớ ọ ∈[u,v]. Khi t’≥ u
thì còn ph i xét bài toán P(0,t) ng v i t ả ứ ớ ∈[u,t’]. Đ làm vi c này ta xu t phát tể ệ ấ ừ
b ng đ n hình hi n có, đ t tả ơ ệ ặ 0 = t’ và tính l i các h s đ c tr ng aạ ệ ố ặ ư m+1,j (t’) = hj+gj.t’,j
=1,2,…,n cũng nh giá tr hàm m c tiêu bư ị ụ m+1(t’) = h0+g0t’. Sau đó s xu t hi n ho cẽ ấ ệ ặ
tr ng h p 2 ho c tr ng h p 3.ườ ợ ặ ườ ợ
iii) gl < 0: Khi đó am+1,l = hl, + gl.t > 0 ng v i m i giá tr c a t < t”, v i ứ ớ ọ ị ủ ớ
0
l
lt
g
h
"t >−=
(2.11)
Suy ra ∀t < t” bài toán P(0,t) có hàm m c tiêu không b ch n d i và do đó khôngụ ị ặ ướ
gi i đ c. N u t”> v, thì bài toán P(0,t) không gi i đ c v i m i tả ượ ế ả ượ ớ ọ ∈[u,v]. Khi t”≤ v
còn ph i xét bài toán P(0,t) ng v i t ả ứ ớ ∈[t”,v]. Đ làm vi c này ta xu t phát t b ngể ệ ấ ừ ả
đ n hình hi n có, đ t tơ ệ ặ 0 = t” và tính l i các h s đ c tr ng aạ ệ ố ặ ư m+1,j(t”) = hj + gj.t” =1,2,
…,n cũng nh giá tr hàm m c tiêu bư ị ụ m+1(t”) = h0 +g0t”. Sau đó s xu t hi n ho cẽ ấ ệ ặ
tr ng h p 2 ho c tr ng h p 3 nh trên.ườ ợ ặ ườ ợ ư
3) Xét tr ng h p 3:ườ ợ
Cũng không làm m t tính t ng quát, gi s l i gi i t i u ấ ổ ả ử ờ ả ố ư x0 t ng ng v i b ng đ nươ ứ ớ ả ơ
hình d ng (2.5). Khi đó các h s đ c tr ng aạ ệ ố ặ ư m+1,j (t0) = hj + gjt0 ≤ 0, j=1,2,…,n. D th yễ ấ
r ng ng v i j, 1ằ ứ ớ ≤ j ≤ n, đi u ki n ề ệ
am+1,j (t) = hj + gjt ≤ 0 (2.12)
v n th a mãn v i m i giá tr t sao cho ẫ ỏ ớ ọ ị
t ≤
j
j
g
h
−
, khi gj > 0,
ho c t ặ≥
j
j
g
h
−
, khi gj < 0.
Đ t ặ
Lê V n Phiă89

Lyù t huyeát qui hoaï ch t uyeán tí nh
t -1 =
n,...,1j,0g,u
)
g
h
(max
j
j
j
0g j
=∀≥
−
<
(2.13)
và
t1 =
n,...,1j,0g,v
)
g
h
(min
j
j
j
0g j
=∀≤
−
>
(2.14)
Khi đó d th y r ng (2.12) th a mãn v i m i j = 1,2,…,n, ng v i các giá tr tễ ấ ằ ỏ ớ ọ ứ ớ ị ∈[t -1 , t1]
và t -1 ≤ t0 ≤ t1. T c là ph ng án ứ ươ x0 hi n có là ph ng án t i u ng v i m i bài toánệ ươ ố ư ứ ớ ọ
P(0,t) v i tớ∈[t -1 , t1]. N u t ế–1 ≤ u và t1 ≥ v thì vi c gi i bài toán tham s P(0,t) k t thúc.ệ ả ố ế
Ng c l i, n u tượ ạ ế –1 > u ho c tặ1 < v thì còn ti p t c kh o sát bài toán P(0,t) ng v i tế ụ ả ứ ớ ∈[u, t -1]
ho c tặ∈[t1 , v]. Khi đó x0 có th không còn là ph ng án t i u c a các bài toán P(0,t)ể ươ ố ư ủ
t ng ng. ươ ứ Ta kh o sát t ng tr ng h p c th :ả ừ ườ ợ ụ ể
a) Tr ng h p tườ ợ 1 < v: Gi s ả ử
0g,
g
h
tr
r
r
1>−=
. Vì gm+r > 0, nên,∀t > t1, am+1,r(t) = hr + gr.t >
am+1,r(t) = hr + gr.t1 = 0. Do đó đi u ki n t i u ng v i ề ệ ố ư ứ ớ x0 không còn th a mãn. N u aỏ ế ir
≤ 0, i = 1,2,…,m thì hàm m c tiêu Z(t) không b ch n d i v i m i giá tr t > tụ ị ặ ướ ớ ọ ị 1. Do đó
P(0,t) ng v i m i tứ ớ ọ ∈(t1,v] không gi i đ c. Ng c l i, gi s ả ượ ượ ạ ả ử ∃p, 1≤ p ≤ m, v i aớpr >
0. Ti p t c th c hi n phép bi n đ i đ n hình v i c t chu n là c t r. T đây s xácế ụ ự ệ ế ổ ơ ớ ộ ẩ ộ ừ ẽ
đ nh ti p tị ế 2 theo (2.14). Ph ng án m i cũng s t i u ng v i tươ ớ ẽ ố ư ứ ớ ∈[t1, t2]. Sau đó, ho cặ
thu t toán k t thúc v i k t lu n P(0,t) ng v i tậ ế ớ ế ậ ứ ớ ∈(t2, v] không gi i đ c ho c xác đ nhả ượ ặ ị
ti p tế3, v.v…
b) Tr ng h p tườ ợ -1 > u: Gi s ả ử
0g,
g
h
tr
r
r
1<−=
−
. Vì gm+r < 0, nên,∀t < t-1, am+1,r(t) = hr + gr.t
> am+1,r(t-1) = hr + gr.t-1 = 0. Do đó đi u ki n t i u ng v i ề ệ ố ư ứ ớ x0 không còn th a mãn. N uỏ ế
air ≤ 0, i = 1,2,…,m thì hàm m c tiêu Z(t) không b ch n d i v i m i giá tr t < tụ ị ặ ướ ớ ọ ị -1. Do
đó P(0,t) ng v i m i tứ ớ ọ ∈(u, t-1] không gi i đ c. Ng c l i, gi s ả ượ ượ ạ ả ử ∃p, 1≤ p ≤ m, v iớ
apr > 0. Ti p t c th c hi n phép bi n đ i đ n hình v i c t chu n là c t r. T đây sế ụ ự ệ ế ổ ơ ớ ộ ẩ ộ ừ ẽ
xác đ nh ti p tị ế -2 theo (2.13). Ph ng án m i cũng s t i u ng v i tươ ớ ẽ ố ư ứ ớ ∈[t-1, t-2]. Sau đó,
ho c thu t toán k t thúc v i k t lu n P(0,t) ng v i tặ ậ ế ớ ế ậ ứ ớ ∈[u, t-2) không gi i đ c ho cả ượ ặ
xác đ nh ti p tị ế -3, v.v…
2.1.2 Ví dụ:
Gi i bài toán QHTT ch a tham s sau đây:ả ứ ố
2t3
7,...,2,1j,0x
5xx3x3x2x
5xx2xx3x2
0xxxx2x
minx)t21(x)t23(x)t2(x)t1()x(f
j
74321
64321
54321
4321
≤≤−
=≥
=+−++−
=++−+
=+−+−
→++−+−+−=
Lê V n Phiă90
Lyù thuyeát qui hoaïch tuyeán tính
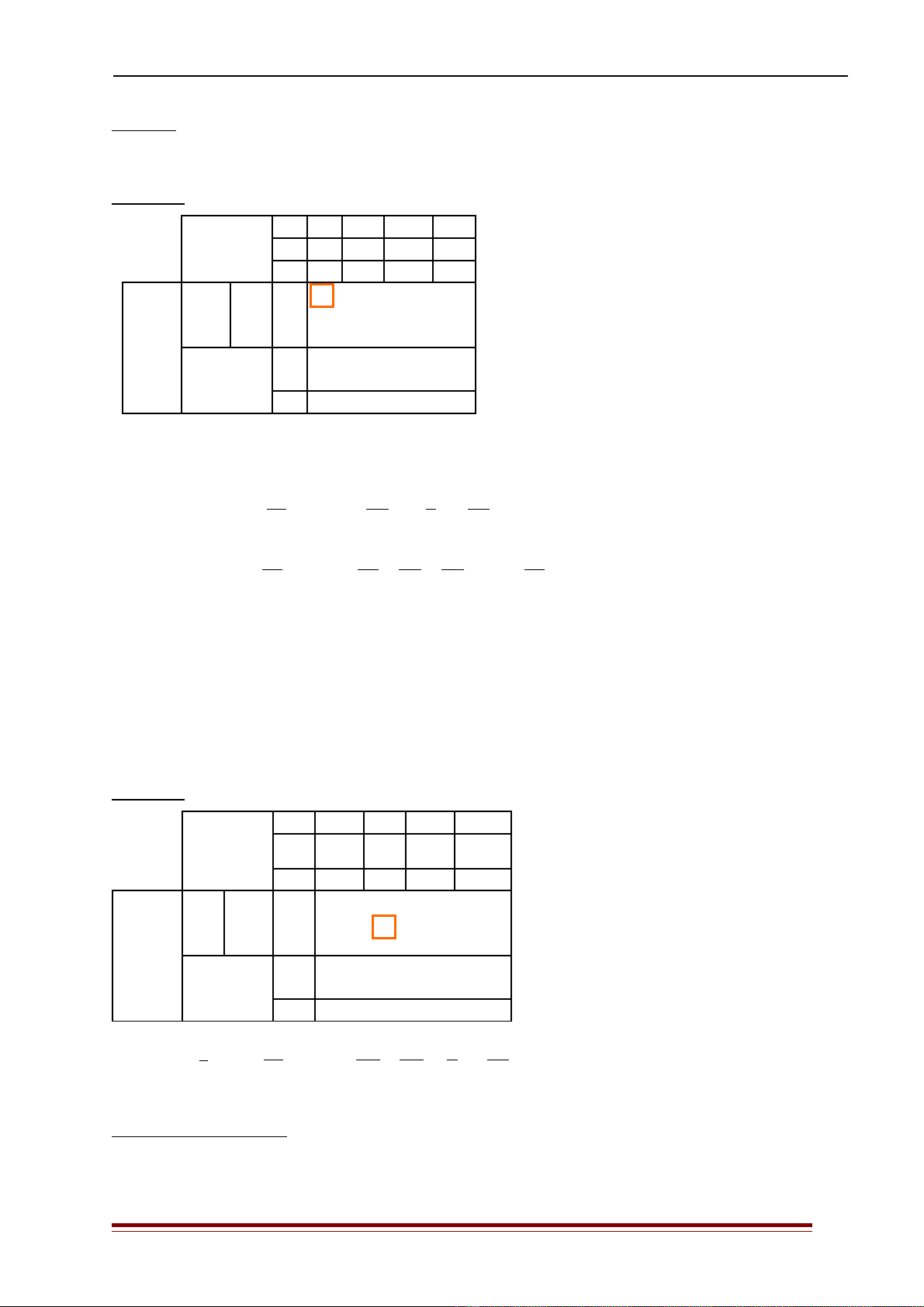
Bài gi iả: Ch n ọt0 = 0. Ph ng án xu t phát v i các bi n c b n xươ ấ ớ ế ơ ả 5 = 0, x6 = 5, x7 = 5 và các
bi n không c b n xế ơ ả 1 = x2 = x3 = x4 = 0. Đây đ ng th i là ph ng án t i u v i Z(xồ ờ ươ ố ư ớ 0,0) = 0.
Ta có b ng đ n hình t ng ngả ơ ươ ứ 27.
B ng 6.1ả:
H s nệ ố ẩ
c sơ ở
cj dj
bix1x2x3x4
cj1 2 3 1
dj-1 -1 -2 2
x50 0 0 1 -2 1 -1
x60 0 5 2 3 -1 2
x70 0 5 -1 2 3 -3
hjt0 = 0 0 -1 -2 -3 -1
gj0 1 1 2 -2
ym+1,j 0 -1 -2 -3 -1
B ng 2.1, ph ng án xu t phát đ ng th i là ph ng án t i u khi tỞ ả ươ ấ ồ ờ ươ ố ư 0 = 0, vì các h sệ ố
đ c tr ng aặ ư m+1,j ≤ 0, j = 1,2,…,n; Z(x0) = 0. Ta xác đ nh các c n tị ậ 1 và t -1 nh sau:ư
,
g
h
2
1
}
2
1
{max
g
h
maxt
4
4
j
j
0g
1
j
−=−=
−
−
−=
−= <
−
,
g
h
1}
2
3
,
1
2
,
1
1
{min
g
h
mint
1
1
j
j
0g
1
j
−==
−
−
−
−
−
−=
−= >
V y là ph ng án ậ ươ x0 = (0, 0, 0, 0, 0, 5, 5) là ph ng án t i u v i m i bài toán P(0,t) trongươ ố ư ớ ọ
kho ng [-1/2, 1]. Chúng ta còn ph i xét P(0,t) trong các kho ng [-3, -1/2) và (1, 2].ả ả ả
Xét kho ng (1, 2]. Th c hi n phép bi n đ i đ n hình v i c t chu n r = 1ta có b ng 2.ả ự ệ ế ổ ơ ớ ộ ẩ ả
Trong b ng này ph ng án t i u v n là xả ươ ố ư ẫ 0, nh ng xư1 tr thành bi n c b n, xở ế ơ ả 5 là bi n phiế
c s . Đ tìm kho ng bi n thiên c a t sao cho xơ ở ể ả ế ủ 0 v n còn là ph ng án t i u ta tính tẫ ươ ố ư 2 như
sau:
B ng 6.2ả:
H s nệ ố ẩ
c sơ ở
cj dj
bix5x2x3x4
cj0 2 3 1
dj0 -1 -2 2
x11 -1 0 1 -2 1 -1
x60 0 5 -2 7 -3 4
x70 0 5 1 0 4 -4
hjt1 = 1 0 0 -4 -2 -2
gj0 0 3 1 -1
am+1,j 0 0 -1 -1 -3
2
2
j
j
0g
2g
h
3
4
}
1
2
,
3
4
min{
g
h
mint
j
−==
−
−
−
−=
−= >
27 Đ đ n gi n, các c t ng v i các bi n c b n không đ c trình bày trong b ng. Ta g i đó là b ng đ n hình rútể ơ ả ộ ứ ớ ế ơ ả ượ ả ọ ả ơ
g n.ọ
Lê V n Phiă91







![Kinh tế số Việt Nam: Chính sách và thực thi [Cập nhật mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2024/20241028/gaupanda058/135x160/4241730112118.jpg)


















