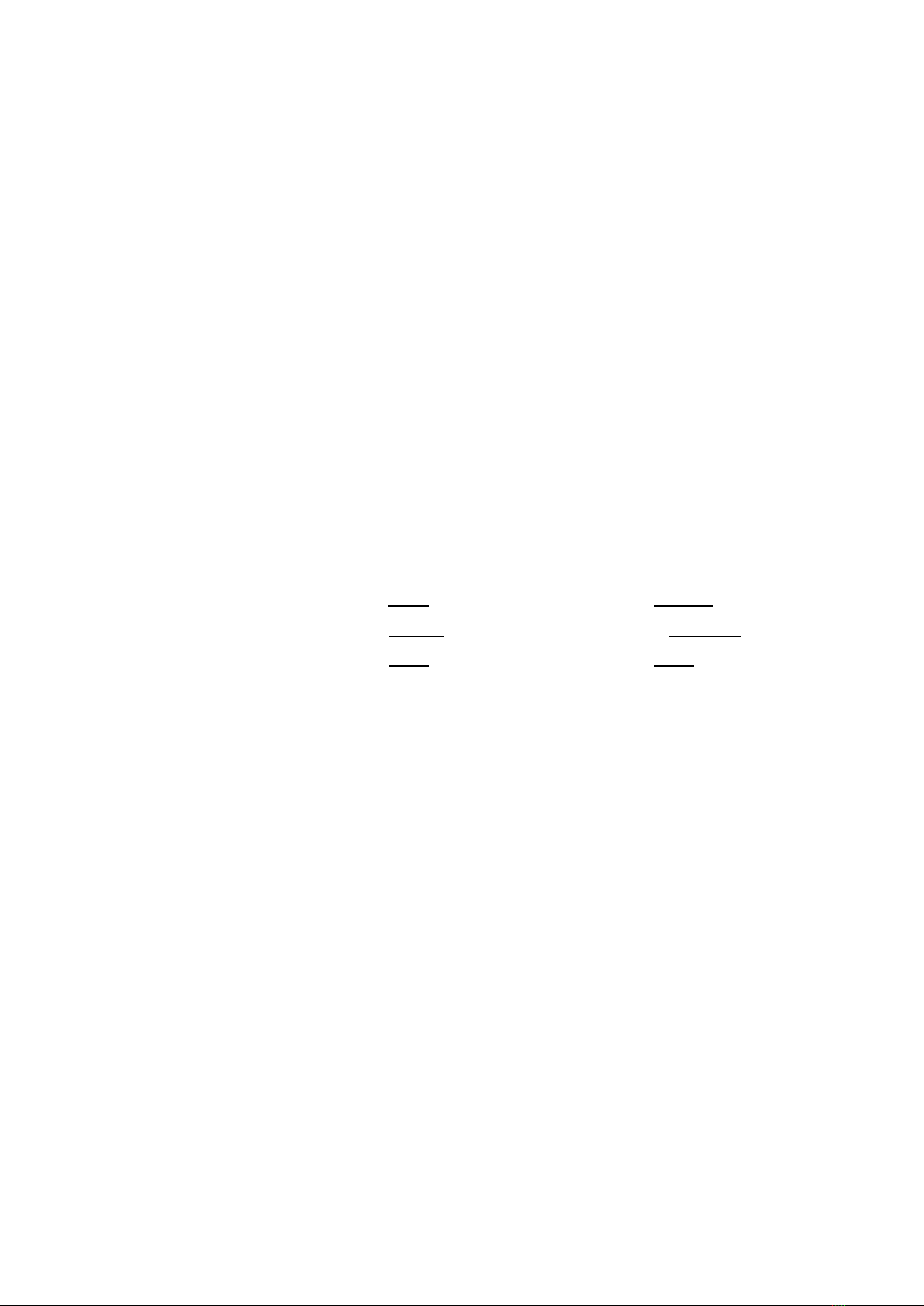MINISTRY OF EDUCATION
AND TRAINING
VIETNAM ACADEMY OF
SCIENCE AND TECHNOLOGY
GRADUATE UNIVERSITY OF SCIENCE AND TECHNOLOGY
________________________________
NGUYEN VAN QUYEN
RESEARCH IMAGE CONTRAST ENHANCEMENT
BASED ON HEDGE ALGEBRA
MATHEMATICS DOCTORAL DISSERTATION
Major: Math Fundamentals for Informatics
Code: 9.46.01.10
SUMMARY OF MATHEMATICS DOCTORAL
DISSERTATION
Ha Noi, 2018
This work is completed at:
Graduate University of Science and Technology
Vietnam Academy of Science and Technology
Supervisor 1: Dr. Tran Thai Son
Supervisor 2: Assoc. Prof. Dr. Nguyen Tan An
Reviewer 1: ……………………………………………………………………
…………………………………………………………………………………
Reviewer 2: ……………………………………………………………………
…………………………………………………………………………………
Reviewer 3: ……………………………………………………………………
…………………………………………………………………………………
This Dissertation will be officially presented in front of the Doctoral
Dissertation Grading Committee, meeting at:
Graduate University of Science and Technology
Vietnam Academy of Science and Technology
At …………. hrs ……. day ……. month……. year …….
This Dissertation is available at:
1. Library of Graduate University of Science and Technology
2. National Library of Vietnam
LIST OF PUBLISHED WORKS
[1]
Nguyen Van Quyen, Tran Thai Son, Nguyen Tan An, Ngo Hoang
Huy and Dang Duy An, “A new method to enhancement the contrast
of color image based on direct method”, Joural of Research and
Development on Information and Communication technology, Vol 1,
No 17 (37): 59-73, 2017
[2]
Nguyen Van Quyen, Ngo Hoang Huy, Nguyen Cat Ho, Tran Thai
Son, “A new homogeneity measure construction for color image direct
contrast enhancement based on Hedge algebra”, Joural of Research
and Development on Information and Communication technology, Vol
2, No 18 (38): 19-32, 2017
[3]
Nguyen Van Quyen, Nguyen Tan An, Doan Van Hoa, Hoang Xuan
Trung, Ta Yen Thai, “Contruct a homogeneity measurement for the
color image bassed on T-norm”, Journal of Military science and
Technology, No 49: 117-131, 2017
[4]
Nguyen Van Quyen, Nguyen Tan An, Doan Van Hoa, Hoang Xuan
Trung, Ta Yen Thai, “A method to construct an extent histogram of
multi channel images and applications”, Journal of Military science
and Technology, No 50: 127-137, 2017
[5]
Nguyen Van Quyen, Tran Thai Son, Nguyen Tan An, Construct an S-
shaped gray-scale transformation function that enhances images
contrast using Hedge Algebra, Proceedings of the 10th National
Conference on Fundamental and Applied Information Technology
Reseach (Fair’ 10), 884-897, Da Nang, 2017
Introduction
Contrast enhancement is a very important issue in processing and
analysing image, is a fundamental step in analyzation and segmentation image.
These are mainly two categories: (1) indirect method of contrast enhancement
and (2) direct method of contrast enhancement.
a) About indirect method
There are many indirect techniques, which were proposed in references.
They only modifies the histogram, without using any contrast measure.
In recent years, many researchers have applied fuzzy set theory to
develope new techniques to enhance the contrast of the image.
Fuzzy approach algorithms often lead to the requirement of designing a
gray-scale transformation S-shape function (The function is continuous
monotonous increase, decreasing the input gray level when the input is below
the threshold, and increasing the value gray level input when the input is above
the threshold). However, the selection of functions in the fuzzy rule inference to
produce the gray-scale transformation S-shape function is not easy. With the
following simple fuzzy rule
R1: If luminance input is dark then luminance output is darker
R2: If luminance input is bright then luminance output is brighter
R3: If luminance input is gray then luminance output is gray
So, the fuzzy reasoning results using fuzzy sets is not obvious and it is quite
difficult to obtain the appropriate gray-scale S-shape function.
b) About direct method
For a long time to date, almost only the studies by Cheng and coworkers
have followed direct approaches, the authors have been proposed a method
which modify the contrast at each pixel of gray-scale image based on the
definition of image’s homogeneity measure.
In addition, Cheng and coworkers have proposed an algorithm that uses
the S-function which have parameters to transform the multi-level gray-scale
input image and then enhance the image’s contrast by direct method.
Cheng's algorithms are the basis of the contrast enhancement of grayscale
images. However, these algorithms still have some limitations when applying to
color images, multichannel images ...:
(i) The resulting image after enhancement the contrast may not change the
brightness of the color compared to the original image.
(ii) Using images that have been modified by Cheng's image modification
method as input of contrast enhancement process may lose details of original
image.
2
For the homogeneity measurement of pixel, Cheng proposed a way to
estimate the homogeneity value of the pixel from local values Eij, Hij, Vij, R4,ij.
When experimenting with color images, we noticed that with this estimate, the
resulting image may not be smooth.
Actually the pixel's homogeneity is a fuzzy value so that we can apply the
fuzzy logic to get this value.
If local values
ij i j
,EH
are passed to computing with word then the formula
is formatted
should reflect the fuzzy rule system as follows:
If
g r a d i e n t
is hight and
e n tr o p y
is hight then homogeneity is hight
If
g r a d i e n t
is low and
e n tr o p y
is low then homogeneity is low
If we add rules with terms like "very", "little", "medium" etc. with
linguistic variables like "homogeneity", "entropy", "gradient" etc then
homogeneity values can be estimated by human inference and thus it will be
finer.
Because fuzzy set theory has no basis form between the relationships of
the linguistic variable with the fuzzy sets and the order of relations between the
words, it is important to consider using a fuzzy reasoning method to ensure
order.
Through surveys, analyses and experiments we have the conclusion:
Firstly, the if-then argument based on the fuzzy set is very difficult to
guarantee the S shape of the gray-scale transformation function. The direct
contrast enhancement method of Cheng uses a transformation gray-scale
function has S-shape but not Symmetric and the gray value may fall outside the
gray-area value.
Secondly, Cheng's homogeneity measurement has still limited, for
example the resulting image may not be smooth.
Thirdly, using Cheng's algorithm directly on the original image channel,
the brightness of the resulting image may be less volatile. In order to change the
brightness, it is necessary to transform the original image before applying
Cheng's contrast enhancement. Cheng's image transform method may cause loss
of detail of the original image.
The research topic of doctoral dissertation is:
Problem 1: Designing the Gray S-type transformation and symmetry.
Problem 2: Constructing a local homogeneity measurement of image.
Problem 3: Constructing fuzzy transformation method for image without
losing details of original image.