
MỤC LỤC
I. ĐẶT VẤN ĐỀ. ...................................................................................................... 1
1. Lí do chọn đề tài. ................................................................................................ 1
2. Mục đích nghiên cứu. ......................................................................................... 2
3. Đối tượng nghiên cứu. ....................................................................................... 2
4. Phương pháp nghiên cứu.................................................................................... 2
5. Giới hạn phạm vi nghiên cứu. ............................................................................ 3
II. NỘI DUNG NGHIÊN CỨU. ............................................................................. 3
1. Cơ sở lí luận của vấn đề ..................................................................................... 3
1.1. Hàm số bậc nhất ........................................................................................... 3
1.2. Hàm số bậc hai ............................................................................................. 4
2. Thực trạng của vấn đề ........................................................................................ 4
3. Các biện pháp đã tiến hành để giải quyết vấn đề. .............................................. 5
3.1. Tiếp cận phương pháp giải và biện luận phương trình có dạng
0ax b
. 5
3.2. Tiếp cận phương pháp giải và biện luận phương trình có dạng
20.ax bx c
................................................................................................... 6
3.3. Tiếp cận phương pháp giải và biện luận bất phương trình có dạng
0.ax b
............................................................................................................ 7
3.4. Tiếp cận phương pháp giải và biện luận bất phương trình có dạng
20.ax bx c
................................................................................................... 7
3.5. Phương pháp giải bài toán liên quan đến phương trình, bất phương trình có
chứa tham số có thể quy về bậc nhất một ẩn. ..................................................... 8
3.6. Thiết kế giáo án dạy học phương trình, bất phương trình bậc nhất và bậc
hai một ẩn thông qua mối liên hệ với hàm số bậc nhất và bậc hai một ẩn ....... 28
4. Kết quả đạt được .............................................................................................. 39
III. KẾT LUẬN ..................................................................................................... 42
TÀI LIỆU THAM KHẢO .................................................................................... 43

1
I. ĐẶT VẤN ĐỀ.
1. Lí do chọn đề tài.
Phương trình, bất phương trình là một trong những chủ đề quan trọng và lâu
đời nhất trong lịch sử toán học. Do đó, giảng dạy phương trình, bất phương trình
luôn có tầm quan trọng dạy học toán ở bất kỳ nền giáo dục nào. Khái niệm phương
trình, bất phương trình đã được đưa vào chương trình toán từ cấp tiểu học dưới hình
thức ngầm ẩn như điền vào ô trống để được đẳng thức đúng, tìm x (trong tập số N),...
Đến cấp trung học cơ sở, trong chương trình lớp 7 có khái niệm về phương trình
ax b
trong tập số hữu tỉ. Khái niệm phương trình, bất phương trình được giới thiệu
tường minh ở lớp 8 và được chính xác hóa trong chương trình toán lớp 10 thông qua
mệnh đề chứa biến hoặc biến của hàm số ban đầu.
Theo cách định nghĩa phương trình dựa vào biến của hàm số ban đầu, trong
chương trình sách giáo khoa môn toán THPT của cả ba khối lớp; bài học phương
trình, bất phương trình luôn được sắp xếp sau bài học về hàm số tương ứng với loại
phương trình đó. Chẳng hạn, lớp 10 có hàm số bậc nhất, bậc hai và phương trình,
bất phương trình quy về bậc nhất, bậc hai một ẩn; lớp 11 có hàm số lượng giác và
phương trình lượng giác; lớp 12 có hàm số mũ, logarit và phương trình, bất phương
trình mũ và logarit. Tuy nhiên, tôi nhận thấy việc dạy và học phương trình, bất
phương trình hiện nay hầu như chỉ tập trung vào các phép biến đổi đại số, các công
thức nghiệm mà chưa tận dụng được hết những tính chất của các loại hàm số đó để
đưa vào bài học phương trình, bất phương trình. Học sinh đã quen thuộc và có xu
hướng chấp nhận các phép biến đổi đó như một lẽ dĩ nhiên mà không hề có tư duy
tìm ra mối liên hệ với kiến thức hàm số vừa học và không hiểu được ý nghĩa của
hàm số đối với phương trình, bất phương trình. Do đó, khi gặp các câu hỏi liên quan
đến phương trình, bất phương trình chứa tham số mà học sinh phải vận dụng tư duy
hàm số như là một công cụ đắc lực để giải quyết thì học sinh thường lúng túng và
gặp nhiều khó khăn và luôn đặt ra câu hỏi: “Tại sao nghĩ và làm được như vậy?”.
Để trả lời được câu hỏi đó trong các giờ dạy, việc bồi dưỡng năng lực tư duy hàm
số và thông qua hàm số để tiếp cận phương trình, bất phương trình tương ứng là một
điều rất cần thiết. Muốn làm tốt được điều đó người thầy không chỉ có phương pháp
truyền thụ tốt mà còn phải có kiến thức vừa chuyên, vừa sâu, dẫn dắt học sinh tìm
hiểu một cách lôgic bản chất của toán học. Từ đó giúp các em có sự say mê trong
việc học môn Toán, để toán học trở nên gần gũi và là sự yêu mến, hứng thú học hỏi,
niềm say mê đối với các em học sinh THPT.
Với nguyện vọng giúp học sinh thay đổi tư duy khi học về phương trình, bất
phương trình tôi tập trung khai thác cách tiếp cận bài học về phương trình, bất
phương trình thông qua mối liên hệ với hàm số. Trước tiên, tôi chỉ khai thác đề tài
này trong khuôn khổ chương trình lớp 10, sau đó sẽ phát triển tiếp đề tài này cho
khối 11,12. Với việc sử dụng phương pháp tiếp cận này, những bài toán về phương

2
trình, bất phương trình sẽ được giải quyết một cách rất tự nhiên, thuần túy, ngắn gọn
và đơn giản. Đó là lí do để tôi chọn đề tài: “Tiếp cận phương trình, bất phương
trình bậc nhất, bậc hai một ẩn thông qua mối liên hệ với hàm số bậc nhất, bậc hai
một ẩn”.
2. Mục đích nghiên cứu.
Với tên đề tài “Tiếp cận phương trình, bất phương trình thông qua mối liên
hệ với hàm số” thì mục tiêu của đề tài được xác định như sau:
Một là, giúp học sinh tiếp cận bài học phương trình, bất phương trình bậc nhất,
bậc hai một ẩn thông qua mối liên hệ với hàm số tương ứng, từ đó giúp các em khắc
sâu kiến thức đã học về hàm số đồng thời hiểu bản chất các kết quả đại số được trình
bày trong sách giáo khoa.
Hai là, giúp học sinh biết kết hợp các phép biến đổi đại số với các ứng dụng
của hàm số trong các bài toán về phương trình, bất phương trình có chứa tham số có
thể quy về dạng bậc nhất, bậc hai một ẩn một cách linh hoạt, hiệu quả.
Ba là, giúp học sinh tránh phải sai lầm thường gặp khi giải các bài toán liên
quan đến phương trình, bất phương trình cần đặt ẩn phụ mà không nghĩ đến tìm điều
kiện của ẩn phụ hoặc tìm sai điều kiện, hoặc đã tìm chính xác điều kiện của ẩn phụ
nhưng khi lập luận trên phương trình, bất phương trình theo ẩn phụ thì lại không xét
trên điều kiện ràng buộc của nó nên dẫn đến kết luận không chính xác. Giúp học
sinh hiểu việc tìm điều kiện của ẩn phụ thực ra là tìm tập giá trị của ẩn phụ trên tập
xác định của bài toán đã cho bằng hàm số. Sau khi tìm được điều kiện của ẩn phụ
thì những yêu cầu của đề bài đối với bài toán theo ẩn chính phải được quy về những
yêu cầu tương ứng cho bài toán theo ẩn phụ trên điều kiện của nó. Đó là điều quan
trọng để chọn đặt hàm số tương ứng trên tập giá trị của ẩn phụ.
3. Đối tượng nghiên cứu.
Trong đề tài này chủ yếu sử dụng các tính chất của hàm số, bảng biến thiên và
đồ thị hàm số để giải toán phương trình, bất phương trình có thể quy về bậc nhất,
bậc hai một ẩn, hệ phương trình, hệ bất phương trình, đặc biệt là các bài toán về
phương trình, bất phương trình, hệ phương trình, hệ bất phương trình có tham số.
4. Phương pháp nghiên cứu.
- Nghiên cứu bằng lí luận dạy và học, nghiên cứu sách giáo khoa, tài liệu tham
khảo.
- Nghiên cứu qua thực tế giảng dạy, ôn thi THPT Quốc gia.
- Nghiên cứu qua kết quả học tập của học sinh về toán phương trình, bất phương
trình, hệ phương trình và hệ bất phương trình.
- Điều tra thống kê, rút kinh nghiệm theo từng đợt khảo sát.
3
5. Giới hạn phạm vi nghiên cứu.
Đề tài này đã được nghiên cứu đối với việc giải toán phương trình, bất phương
trình, hệ phương trình và hệ bất phương trình chứa tham số bằng cách sử dụng hàm
số đối với học sinh lớp 10.
II. NỘI DUNG NGHIÊN CỨU.
1. Cơ sở lí luận của vấn đề
1.1. Hàm số bậc nhất
a. Định nghĩa: Hàm số bậc nhất là hàm số có dạng
y ax b
( 0)a
.
b. Sự biến thiên
TXĐ : D = R
Chiều biến thiên
Với a > 0 hàm số đồng biến trên R
Với a < 0 hàm số nghịch biến trên R
Bảng biến thiên
a > 0
x
- +
y
+
-
a < 0
x
- +
y
+
-
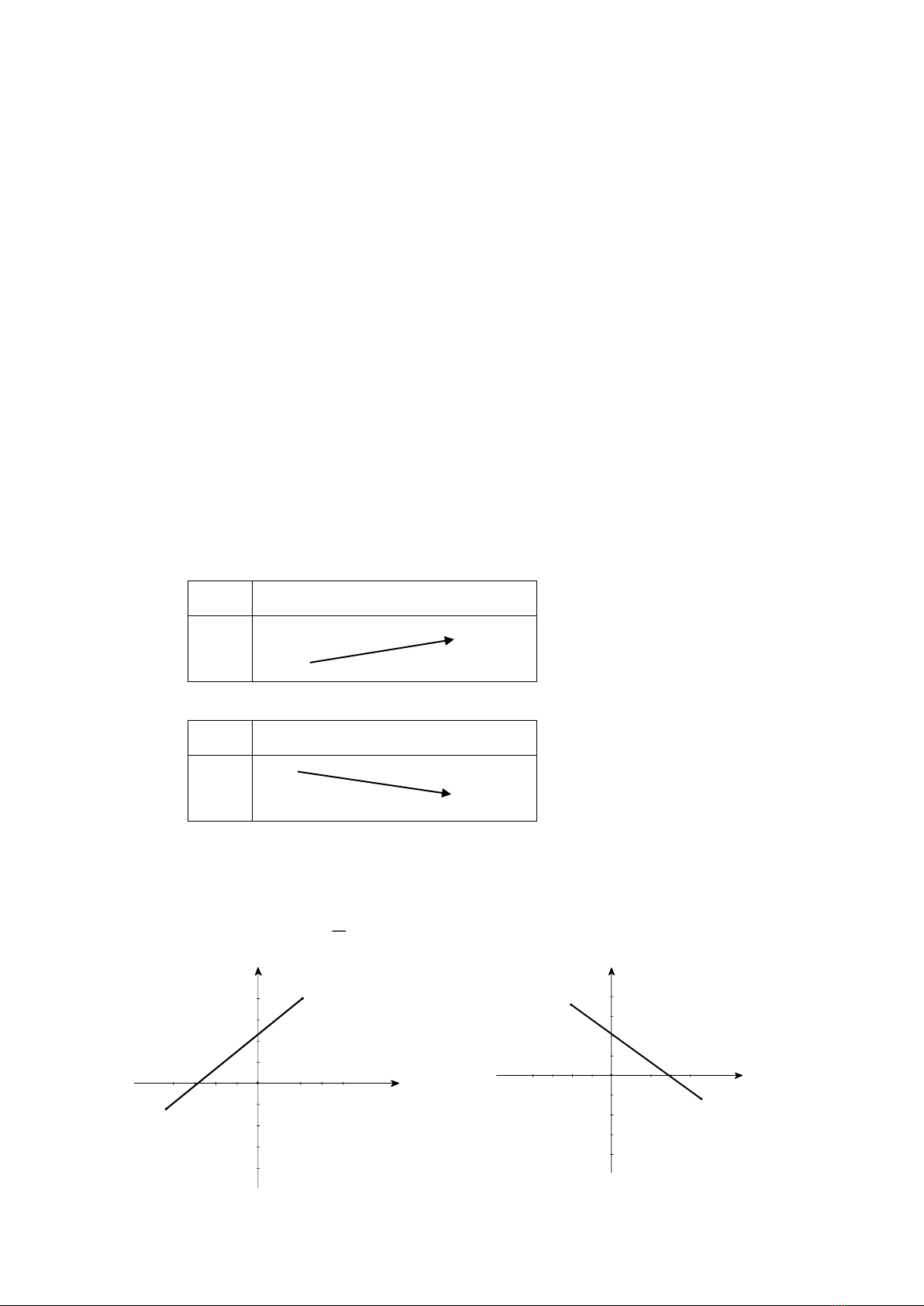
c. Đồ thị
Đồ thị của hàm số
y ax b
( 0)a
là một đường thẳng có hệ số góc bằng
a
,
cắt trục hoành tại
;0
b
Aa
và trục tung tại
0;Bb
x
y
y = ax + b
a > 0
O
x
y
y = ax + b
a < 0
O
4
1.2. Hàm số bậc hai
a. Định nghĩa: Hàm số bậc hai là hàm số có dạng
2() 0y ax bx c a
b. Sự biến thiên:
Tập xác định:
D
Bảng biến thiên
a > 0
x
-
2
b
a
+
y
+ +
4a
a < 0
x
-
2
b
a
+
y
4a
- +
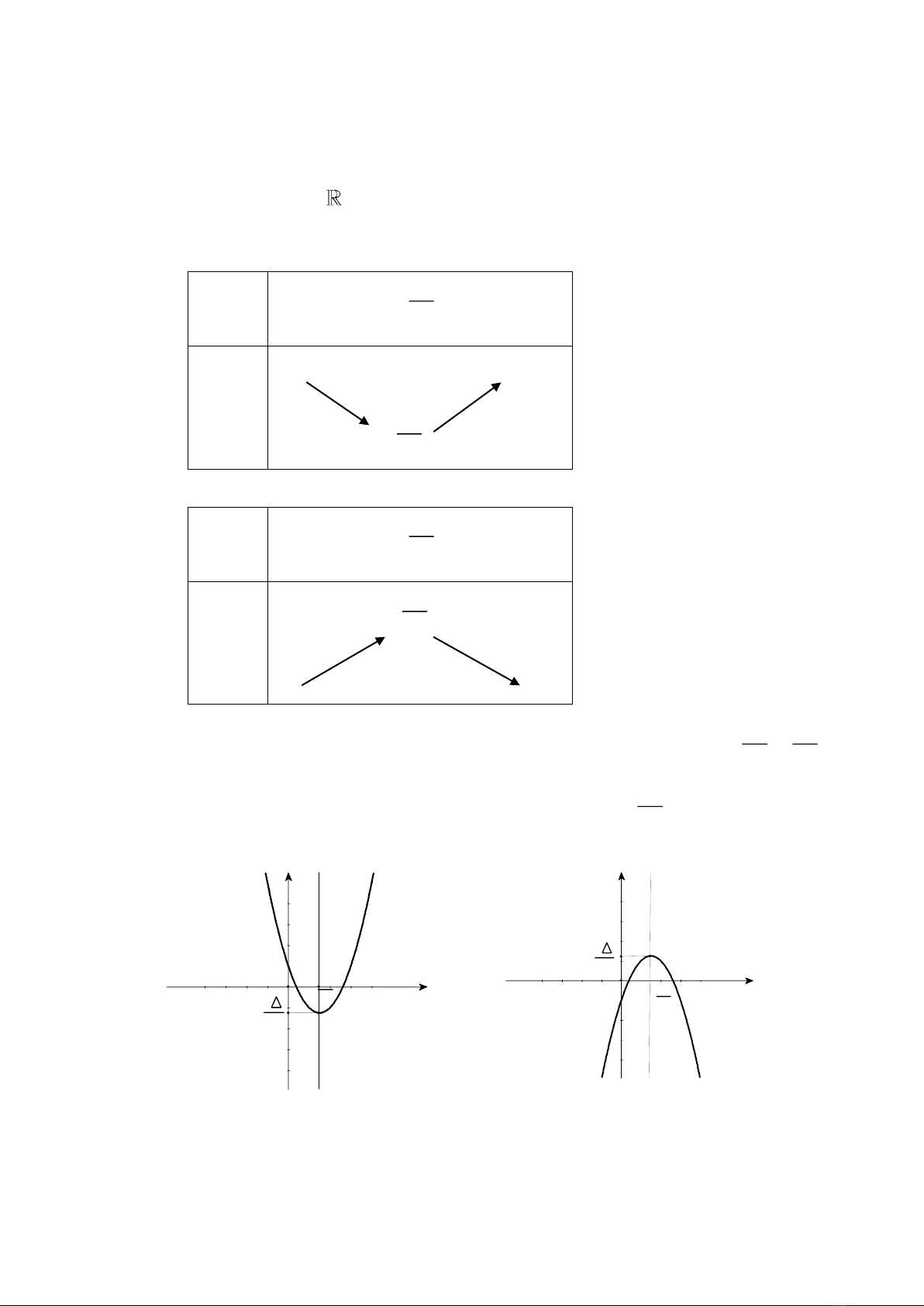
c. Đồ thị : Đồ thị hàm số là một đường Parabol có đỉnh là điểm
;
24
b
Iaa
( = b2 – 4ac), có trục đối xứng là đường thẳng
2
b
xa
. Parabol này quay bề
lõm lên trên nếu a > 0, xuống dưới nếu a < 0.
2. Thực trạng của vấn đề
Qua thực tiễn giảng dạy, tội nhận thấy các tính chất của hàm số và đồ thị hàm
số chưa được nhấn mạnh trong mối quan hệ với phương trình, bất phương trình kể
x
y
a > 0
-
4a
-
b
2a
O
x
y
a < 0
-
4a
-
b
2a
O
















