Simulation of heat exchange between transmission units of an automotive truck

Chia sẻ: Nguyễn Thảo | Ngày: | Loại File: PDF | Số trang:11

Thêm vào BST

Báo xấu

17
lượt xem 3
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

This article details the approach to minimize energy expenditures when using vehicle transmissions. This approach comprises certain mathematical simulation techniques which help to study and minimize energy expenditures of transmission unit systems.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Simulation of heat exchange between transmission units of an automotive truck

International Journal of Mechanical Engineering and Technology (IJMET) Volume 10, Issue 03, March 2019, pp. 1135–1145, Article ID: IJMET_10_03_116 Available online at http://www.iaeme.com/ijmet/issues.asp?JType=IJMET&VType=10&IType=3 ISSN Print: 0976-6340 and ISSN Online: 0976-6359 © IAEME Publication Scopus Indexed SIMULATION OF HEAT EXCHANGE BETWEEN TRANSMISSION UNITS OF AN AUTOMOTIVE TRUCK Dolgushin А.А. Candidate of Technical Sciences, Assistant Professor, Novosibirsk State Agricultural University, Novosibirsk, Russian Federation Voronin D.M. Doctor of Technical Sciences, Professor, Novosibirsk State Agricultural University, Novosibirsk, Russian Federation Mamonov O.V. Lecturer, Novosibirsk State Agricultural University, Novosibirsk, Russian Federation ABSTRACT This article details the approach to minimize energy expenditures when using vehicle transmissions. This approach comprises certain mathematical simulation techniques which help to study and minimize energy expenditures of transmission unit systems. The use of mathematical simulation, when defining an optimum temperature of a transmission unit system, is based on comparison of stabilization temperatures in real conditions, changeover points and optimum temperatures of transmission units. As a criterion of optimization, we suggest using minimization of a resource expenditure function for a whole system of units. This article details possible variants of heat interaction between units and provides guidelines for achieving a target changeover point of a vehicle transmission. We studied possible variants of heat interaction between units and provided recommendations for achieving a target changeover point of a vehicle transmission. Key words: transmission, heat interaction between units, heat exchange simulation, optimum temperature, changeover point, heat distribution. Cite this Article: Dolgushin А.А., Voronin D.M., Mamonov O.V., Simulation of Heat Exchange Between Transmission Units of an Automotive Truck, International Journal of Mechanical Engineering and Technology 10(3), 2019, pp. 1135–1145. http://www.iaeme.com/IJMET/issues.asp?JType=IJMET&VType=10&IType=3 1. INTRODUCTION Nowadays, vehicle efficiency is determined by the amount of resources spent and the volume of wastes produced per run unit of work unit. The main consumable resource is energy generated by an IC engine by burning engine fuel. The amount of consumable fuel depends on http://www.iaeme.com/IJMET/index.asp 1135 editor@iaeme.com
Simulation of Heat Exchange Between Transmission Units of an Automotive Truck the amount of work and energy losses in transmission units. Besides, the amount of combustible fuel determines the amount of hazardous substances emitted by a vehicle to the environment along with exhaust gases. This gets even worse at low temperatures as lubrication oil viscosity is higher. Based on the research findings [1,2], using vehicles under subzero conditions increases engine fuel consumption by 7–9 %. Research by W. Frank shows a significant increase in CO2 emission at subzero temperatures [3]. According to research data [4], when ambient temperature reaches 20 С below zero, CO2 emissions from a moving vehicle increase by 5 %. Furthermore, the need for additional engine warm-up leads to additional emissions of pollutants [5]. Despite of numerous studies on resource saving during use of vehicles, energy losses associated with operation of transmission units were considered negligible, and most of these studies focus on ways to increase engine efficiency. However, continuous increase in costs of energy resources, environmental law enforcement and higher penalties for contamination of the environment make researchers to turn their attention to operational efficiency of transmission units. According to the given data [6], one light motor vehicle consumes an average of 340 l of engine fuel per year to overcome friction forces in transmission units. Given the number of vehicles in the world, they consume up to 208 000 m litres of gasoline and diesel fuel to overcome friction forces. Studies of energy transfer through transmission reduction gears show that mechanical friction in gears and oil churning are the main reasons for energy losses [7,8]. At positive temperatures 52 % of total losses comes to mechanical friction, and 40 % to oil churning [9]. At subzero temperatures the percentage of losses due to oil churning and splashing rises, as oil viscosity is higher. At the current level of science and technology it is obviously impossible to avoid power losses in transmission units. However, some works [10,11] indicate there is potentially a possibility to reduce losses up to 50 %. One of the ways to do that is to improve design of transmission reduction gears. According to the work [12], replacing standard spur gears with skew gears leads to a successful energy loss reduction. Use of gears with shorter teeth helps to reduce friction and decrease unit temperature by 20 %. From the perspective of vehicle owners, methods which would help to reduce losses in real operating conditions are of most interest. Among them is the use of low-viscosity lubrication oils. Replacing the standard oil with a test oil helped to reduce friction in gears by 16–19 % [13]. However, this result occurs only in a limited temperature range. Another way to reduce power losses is regulation of a thermal regime of transmission units by using various technical devices. In production environment, we usually talk about external sources of thermal energy which can use vapour-air mixture [14] or exhaust gas heat [15] as heat conductor. The work [16] proves that the critical factor for reduction of power losses in transmission is monitoring and ensuring the thermal regime of all transmission units. At the first stage, the solution comprises justification of the optimum thermal operating regime of transmission reduction gears in terms of energy expenditures. The work [17] determines an optimum regime as a thermal regime of a unit which correlates with minimum energy resource expenditures to ensure this thermal regime and resource expenditures to overcome a friction torque in the unit. At the second stage, there is a need to justify a temperature range of units which ensures minimum resource expenditures, as well as to develop a strategy to achieve these temperatures within the transmission unit system. http://www.iaeme.com/IJMET/index.asp 1136 editor@iaeme.com
Dolgushin А.А., Voronin D.M., Mamonov O.V. The objective of this work is to develop mathematical models of heat exchange between transmission units which would help to simulate thermal interaction within the unit system, justify target temperature levels and the strategy to achieve them. 2. MATERIALS AND METHODS Apart from the optimum operating regime of a unit, other important features are steady running conditions of the unit and its temperature stabilization regime. The stabilization regime of a unit is characterized by some conditional temperature constancy. By the stabilization regime we mean an operating regime of a unit characterized by equality between heat, that enters the unit, and heat that goes from its surface to the environment. The stabilization temperature value depends on environmental conditions, operating regime of the unit, design and configuration of the transmission, etc. Beside two temperature regimes, we have to take into consideration minimum and maximum operating temperatures of a unit. If stabilization and optimization temperatures go beyond allowable operating regimes, then minimization and stabilization regimes should not be considered while minimizing expenditures. Some adjustments in terms of expenditure minimization should be made here, keeping in mind that these adjustments should be directed towards optimization. Temperature limitations are conditioned by viscosity-temperature properties of the lubricant oil used in transmission. 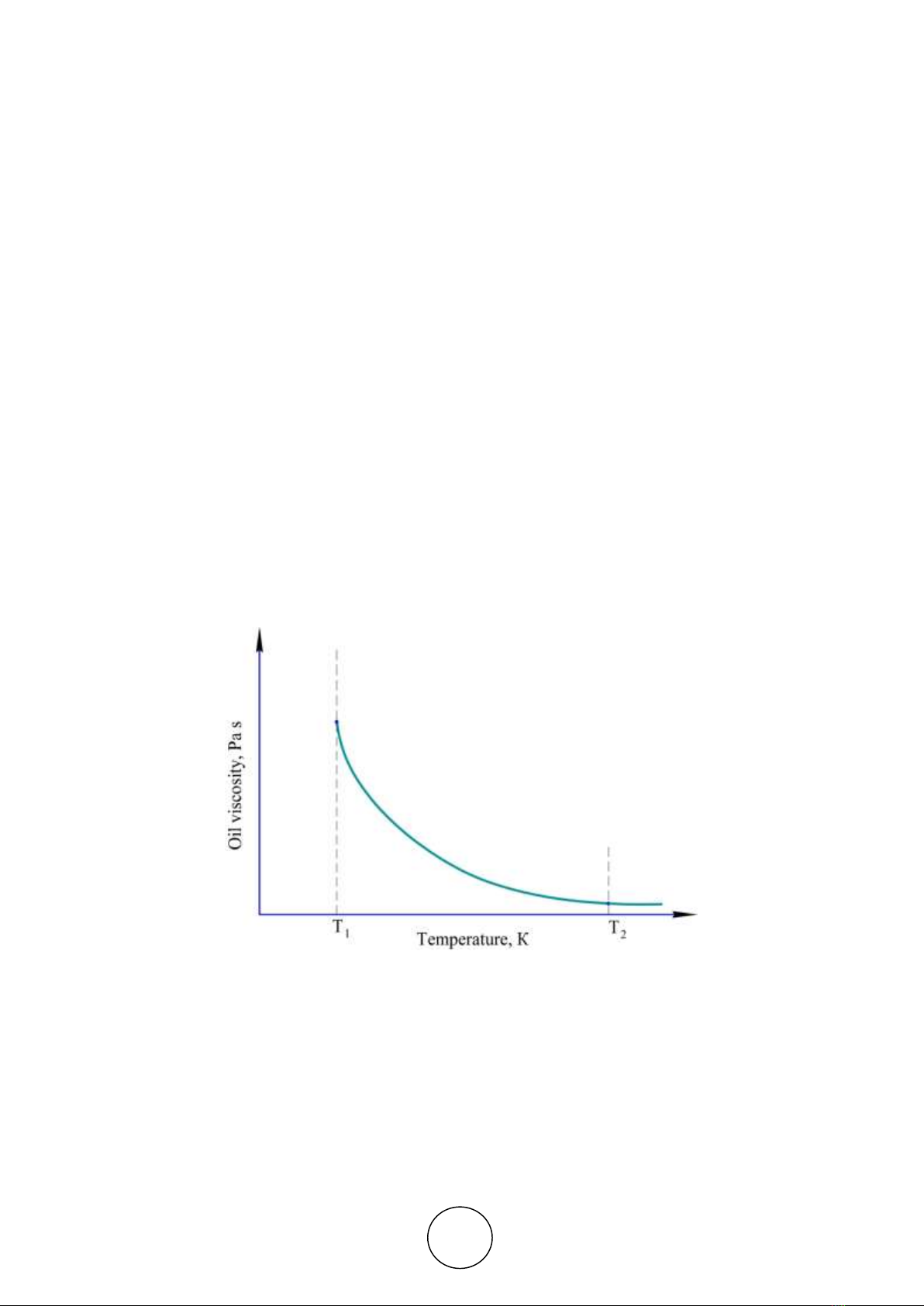In general, the temperature range is limited by the oil temperature that corresponds with the minimum oil viscosity needed for an accident-free start of a vehicle and by the oil temperature that causes a significant decrease in viscosity change rate accompanied by a temperature raise (Fig. 1). Figure 1. Dependency of oil viscosity on temperature — General View In these conditions, if the target optimum temperature of a reduction gear is lower than the final pre-heat temperature Тopt≤Т1, then Т1 shall be considered the optimum temperature. If the equation is Тopt≥Т2, then Т2 shall be considered optimum. We take the stabilization regime as an initial operating regime. Expenditures are minimized when the unit temperature goes from the stabilization temperature to the temperature needed for expenditure optimization. Here we shall make some adjustments within allowable regimes. Each unit has its optimum temperature regime, conditioned by the intent of the given unit and its performance features. To ensure such temperature regime means to use the unit to its http://www.iaeme.com/IJMET/index.asp 1137 editor@iaeme.com
Simulation of Heat Exchange Between Transmission Units of an Automotive Truck full capacity. The optimum thermal regime of a unit is however just conditionally optimum, and reflects neither real work of the unit nor its interaction with other units. That is why determination and further maintenance of the rational thermal regime of vehicle units as a whole are important, both scientifically and practically. This being so, a system is divided into subsystems, and it is expected that thermal regime affects only subsystem units. Each subsystem in its thermal regime may be looked at independently. Let's divide a system of units into subsystems with observationally equivalent thermal regimes. Then define a resource expenditure function for the whole system: S=S(x1 ;x2 ;…,xn )=S1 (x1 ;x2 ;…,xn )+S2 (x1 ;x2 ;…,xn )+…+Sk (x1 ;x2 ;…,xn ), (1) where: x1, x2, … , xn – are values, representing thermal regimes of units; Sj (x1;x2;…;xn) – expenditure functions for various resources; j=1, 2, …, k are types of resources used to ensure the thermal regime. Expenditures (1) are determined for the following constraint system: (1) Тmin ≤Т (1) (x1 ;x2 ;…,xn ) ≤ Т(1) max (2) Тmin ≤ Т(2) (x1 ;x2 ;…,xn ) ≤ Т(2) max (2) … (m) (m) (m) {Тmin ≤ Т (x1 ;x2 ;…,xn ) ≤ Тmax where: Т(i) (x1; x2; … ; xn) – are thermal regimes of units, i=1, 2, …, m; Тmin(i) and Тmax(i) – are minimum and maximum temperature values of given units, i=1, 2, …, m. Via Ti (temperature of the i-unit) we can determine S(i) — total costs of using the i-unit at the unit's temperature Ti, i=1, 2, …, m. Thus, minimization of resource expenditures involves (1) (2) determination of temperature intervals from Тi to Тi for each unit. Achievement of such interval during heat exchange will lead to minimization of all resource expenditures S=S(x1 ;x2 ;…,xn ). While studying thermal regimes of a vehicle, we used simulation methodology at large. Taking into consideration operating features and characteristics of units, we used methods of mathematical simulation to design a math model of thermal regimes of units included into an airtight unit system. Optimization of thermal regimes of transmission units was performed with respect to minimization of resource expenditures. By using an expenditure function analysis technique and mathematical analysis methods, we managed to determine the way this function changes depending on a thermal regime of each particular unit and a system of units as a whole. Relying on the methods of determination of the object system temperature, we defined changeover points of a system of units in various states and with various system features. 3. FINDINGS AND CONSIDERATIONS To determine thermal operating regimes of units let's discuss temperature characteristics of each unit and relations between them. It is worth reminding that we talk about four characteristics here: optimum regime temperature, stabilization regime temperature, temperature interval of operation, minimum and maximum operating temperatures of a unit. Let's label them opt respectively: Тi , Тstabil i , Тmin max i , Тi . For each unit we also determine its current temperature in real time t: Ti (t). Further on, if the time is not specified, the temperature of a unit will be Ti. http://www.iaeme.com/IJMET/index.asp 1138 editor@iaeme.com
Dolgushin А.А., Voronin D.M., Mamonov O.V. Thermal regimes are marked on the 0Ti axis (unit temperature), Fig. 2. The figure also shows opt the direction of total expenditure decrease from Тstabil i to Тi . Figure 2. Thermal regimes of the i-unit and direction of total expenditure decrease The Figure 2 illustrates the case when optimum and stabilization operating regimes of a unit are within an allowable range. Let's discuss cases when this requirement is not met, e.g. when opt Тi ≤Тstabil i . When there is no overlap between the allowable regime interval [Тmin i ; Тi max ] and the opt stabil optimum-stabilization temperature regime interval [Тi ; Тi ], then the allowable regime interval shall be considered optimum. The direction of expenditure decrease depends on the position of intervals. If the interval opt [Тi ; Тstabil i ] lies to the left of the interval [Тmin max i ; Тi ] (Fig. 3), the direction shall be from Тmax i min opt stabil min max to Тi . If the interval [Тi ; Тi ] is to the right of [Тi ; Тi ], then expenditure minimization is from Тi to Тi (Fig. 4). The case when Топт min max ст i >Тi does not affect the approach to determination of the direction of expenditure decrease. opt Figure 3 Thermal regimes of the i-unit when the interval [Тi ; Тstabil i ] is to the left of [Тmin max i ; Тi ] opt Figure 4 Thermal regimes of the i-unit when the interval [Тi ; Тstabil i ] is to the right of [Тmin max i ; Тi ] Let's now discuss overlapping of intervals. opt Assume that Тi ≤Тstabil i . In this case heat exchange is controlled by decreasing temperature of a unit (heat transfer or cooling). Here, the minimum optimization interval value is max opt (Тmin i ;Тi ), and the maximum value is min(Тi ;Тi max stabil ). opt If Тi >Тstabil i , then control is performed by increasing the unit temperature (heat input or warm-up). The minimum optimization interval value is max (Тmin i ;Тi stabil ), and the maximum max opt value is min(Тi ;Тi ). http://www.iaeme.com/IJMET/index.asp 1139 editor@iaeme.com
Simulation of Heat Exchange Between Transmission Units of an Automotive Truck Further on, we will address this interval as the optimization interval of the i-unit, and its threshold values as optimum regime and stabilization regime temperatures. Now, let's turn to the process of heat exchange within the system of transmission units and between units and the environment by looking at a tandem drive three-axle truck. In this case the main components are a speed-change gearbox, an intermediate axle and a rear axle. Due to design similarities of intermediate and rear axles (equal mass, identical materials, same dimensions, etc.), the system of transmission units of such vehicle can be presented as a two- unit system: gearbox and drive axles. Thus, the heat exchange equation for the system of units looks as follows:  ΔQ1+ΔQ2–ΔQenv=0, J (3) where: ΔQ1 – is the amount of heat released by the first unit to the system, J; ΔQ2 – is the amount of heat released by the second unit to the system, J; ΔQenv – is heat losses due to interaction with the environment, J. We believe that if heat is absorbed by the i-unit, the ΔQi value is negative, and a negative ΔQenv value means that heat is transferred to the system of units from the environment. At low ambient temperatures heat losses are significant and relatively similar to the amount of heat emitted by the system. Thus, it makes sense to discuss cases when the system of units is thermally isolated from the environment or heat losses to the environment are insignificant. Let's look at an ideal case of heat exchange when no heat is lost to the environment, i.e. ΔQenv=0. The heat exchange equation is as follows: ΔQ1+ΔQ2=0, J (4) We think that the first unit is a heat source, and the second one is a heat consumer. Then we get the following equation of heat balance for the whole system: ΔQ1=ΔQ2, J (5) where: ΔQ2 – is the amount of heat the second unit gets during heat exchange, J. According to the physical meaning, the amount of heat generated by the first unit to the system and the amount of heat the second unit gets from the system can be defined by the following linear equation: ΔQ1 =ccap-1 Ма1 (Т1 -Т), J (6) ΔQ2 =ccap-2 Ма2 (Т-Т2 ), J (7) where: сcap-i – is a specific heat capacity of the multicomponent i-unit, J/(kg K); Маi – is the weight of the i-unit, kg; Т – is a changeover point of the unit system, K; Тi – is the initial temperature of the i-unit, K. We believe that heat exchange in the unit system takes place when units reach a changeover point. Thereupon, temperatures of Т1 and Т2 units in equations (6) and (7) are none other than stabilization regime temperatures of units Тstabil1 and Тstabil 2 . Thus, we can find the system changeover point based on the equation of the system thermal balance (5): ccap-1 Ма1 Тstabil i , + ccap-2 Ма2 Тstabil 2 , Т= =Тc/o, K (8) ccap-1 Ма1 +ccap-2 Ма2 http://www.iaeme.com/IJMET/index.asp 1140 editor@iaeme.com
Dolgushin А.А., Voronin D.M., Mamonov O.V. Let's take a look at an isolated two-unit system in terms of expenditure minimization. Let opt opt Т1 and Т2 be temperatures of unit regimes in which total operating expenditures are minimum. These temperatures shall be defined with account of the adjustment described for a given unit. Let's discuss relations between stabilization temperatures and optimum temperatures of units on the assumption that Тstabil 1 >Тstabil 2 , where stabilization temperature is the second threshold value of the selected range of the given interval. Let's call it stabilization temperature to show that expenditure minimization takes place when the temperature changes from stabilization to optimum. opt opt Case 1. Тstabil 1
Simulation of Heat Exchange Between Transmission Units of an Automotive Truck Figure 5. Diagram of thermal regimes of units in the system There are three possible types of relations between the changeover point and the optimum opt opt opt opt temperature of given units: Tc/o>Т1 , Т2 ≤Tc/o≤Т1 , Tc/oТ1 , then Tc/o>Т2 . During heat exchange between two units, the first opt unit cannot reach the Т1 temperature. That is why minimum expenditures for the first unit are observed at Tc/o. The second unit reaches the Топт2 temperature during heat exchange. This temperature determines minimum expenditures for the second unit. The first unit temperature is Тc/o c/o 1 . Let's mark Tc/o and Т1 on the diagram of thermal regimes (Fig. 6). The minimum of total resource expenditures S1(T1)+S2(T2) for the first unit is within the Tc/o ≤T1 ≤Тc/o 1 interval, opt and within the Т2 ≤T2≤Tc/o interval for the second unit. opt Figure 6. Diagram of thermal regimes at Tc/o >Т1 http://www.iaeme.com/IJMET/index.asp 1142 editor@iaeme.com
Dolgushin А.А., Voronin D.M., Mamonov O.V. opt opt Case 1.2. Let's discuss the case when Т2 ≤Tc/o≤Т1 . The following figure illustrates thermal regimes in this case (Fig. 7): opt opt Figure 7. Diagram of thermal regimes at Т2 ≤Tc/o≤Т1 c/o c/o opt c/o opt Given the temperature Т1 , there are two options: Т1 ≥Т1 и Т1
Simulation of Heat Exchange Between Transmission Units of an Automotive Truck It is possible to minimize resource expenditures during use of vehicle transmissions through management of thermal operating regimes of transmission units. We have suggested a thermal regime mathematical model for a system of transmission units, based on experimental and theoretical determination of changeover points and optimum temperatures of transmission units in question. We have discussed the use of heat exchange between units and determined intervals of thermal regimes in which total operating expenditures of transmission are minimum. We have justified structural solutions based on the idea of combining units into a thermal system by using additional airtight technical devices on a vehicle. For situations where heat exchange between units cannot minimize energy expenditures, we suggest including an additional heat source or a cooler into the system of transmission units. By ensuring the system's target changeover point, it is possible to minimize energy expenditures on transmission units, which leads to reduce consumption of engine fuel and minimize environmental impact. REFERENCES [1] Anisimov, I., Ivanov, А., Chikishev, Е., Chainikov, D., Reznik, L. and Gavaev, А. Assessment of adaptability of natural gas vehicles by the constructive analogy method. International Journal of Sustainable Development and Planning, 12(6), 2017, pp. 1006- 1017. [2] Weilenmann, M., Favez, J.-Y. and Alvarez, R. Cold-start emissions of modern passenger cars at different low ambient temperatures and their evolution over vehicle legislation categories. Atmospheric Environment, 43(15), 2009, pp. 2419–2429. [3] Frank, W. A novel exhaust heat recovery system to reduce fuel consumption. Proceedings of the World Automotive Congress, FISITA, London, England, 2010, pp. 1-10. [4] Chainikov, D., Chikishev, E., Anisimov, I. and Gavaev A. Influence of ambient temperature on the CO2 emitted with exhaust gases of gasoline vehicles. Innovative Technologies in Engineering VII International Scientific Practical Conference, Conference Proceedings, National Research Tomsk Polytechnic University, 2016. p. 12109. [5] Merkisz, J., Pielecha, I., Pielecha, Ja. and M. Szukalski Exhaust emission from combat vehicle engines during start and warm-up. Transport Problems, 6(2), 2011, pp. 121–126. [6] Holmberg, K., Andersson, P. and Erdemir A. Global energy consumption due to friction in passenger cars. Tribology international, 47, 2012, pp. 221–234. [7] Seetharaman, S., Kahraman, A., Moorhead, M. D., and Petry-Johnson, T. T. Oil Churning Power Losses of a Gear Pair: Experiments and Model Validation. ASME J. Tribol, 131(2), 2009, p. 022202. [8] Patel, D.P. and Patel, J.M. An experimental investigation of power losses in manual transmission gear box. International Journal of Applied Research in Mechanical Engineering, 2(1), 2012. pp. 1–5. [9] Molari, G. and Sedoni E. Experimental evaluation of power losses in a power-shift agricultural tractor transmission. Biosystems engineering, 100(2), 2008, pp. 177–183. [10] Höhn, B.-R., Michaelis, K., and Hinterstoißer, M. Optimization of gearbox efficiency. Goriva Maziva, 48(4), 2009, pp 462–480. [11] Michaelis, K., Höhn, B.R. and Hinterstoißer, M. Influence factors on gearbox power loss. Industrial Lubrication and Tribology, 63(1), 2011, pp. 46–55. [12] Magalhães, L., Martins, R., Locateli, C. and Seabra, J. Influence of tooth profile and oil formulation on gear power loss. Tribol, 43, 2010, pp. 1861–1871. http://www.iaeme.com/IJMET/index.asp 1144 editor@iaeme.com
Dolgushin А.А., Voronin D.M., Mamonov O.V. [13] Nirvesh, S. Mehta, Nilesh, J. Parekh and Ravi, K. Dayatar Improve the Thermal Efficiency of Gearbox Using Different Type of Gear Oils. International Journal of Engineering and Advanced Technology, 2(4), 2013, pp. 120-123. [14] Gabitov, I.I., Negovora, A.V., Khasanov, E.R., Galiullin, R.R., Farhshatov, M.N., Khamaletdinov, R.R., Martynov, V.M., Gusev, D., Yunusbaev, N.M. and Razyapov, M.M. Risk reduction of thermal damages of units in machinery heat preparation for load acceptance. Journal of Engineering and Applied Sciences, 14(3), 2019, pp. 709–716. [15] Dolgushin, А.A, Voronin, D.M., Gus'kov, Y.A. and Kurnosov, A.F. Engine exhaust heat recovery. Scientific and technical achievements of AIC, 30(8), 2016, pp. 87–90. [16] Douglas, CE and Thite, A Effect of lubricant temperature and type on spur gear efficiency in racing engine gearbox across full engine load and speed range. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 229(9), 2015, pp. 1095–1113. [17] Dolgushin, A.A., Voronin, D.M. and Mamonov O.V. Methodology of justification for transmission unit thermal regimes. Scientific and technical achievements of AIC, 32(9), 2018, pp. 89–92. http://www.iaeme.com/IJMET/index.asp 1145 editor@iaeme.com