TRẦN CÔNG NGHỊ
HƯỚNG DẪN GIẢI BÀI TẬP
LÝ THUYẾT ĐÀN HỒI
VÀ
CƠ HỌC KẾT CẤU
(TÀI LIỆU HỌC TẬP DÀNH CHO SINH VIÊN
KHOA ĐÓNG TÀU VÀ CÔNG TRÌNH NỔI)
THÀNH PHỐ HỒ CHÍ MINH 6 – 2009
ĐẠI HỌC GIAO THÔNG VẬN TẢI TP HỒ CHÍ MINH
3
Trang này để trống
4
Chương 1
LÝ THUYẾT ĐÀN HỒI
Tóm tắt
Phương trình cân bằng:
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
=+
∂
∂
+
∂
∂
+
∂
∂
=+
∂
∂
+
∂
∂
+
∂
∂
=+
∂
∂
+
∂
∂
+
∂
∂
0
0
0
Z
yxz
Y
zxy
X
zyx
yz
zx
z
yzyxy
xz
xy
x
τ
τ
σ
ττσ
τ
τ
σ
(1.1)
trong đó X, Y, Z – lực khối.
Phương trình biến dạng:
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎟
⎠
⎞
⎜
⎝
⎛+=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+=
=
=
=
x
w
z
u
y
w
z
v
x
v
y
u
z
w
y
v
x
u
zx
yz
xy
z
y
x
∂
∂
∂
∂
γ
∂
∂
∂
∂
γ
∂
∂
∂
∂
γ
∂
∂
ε
∂
∂
ε
∂
∂
ε
(1.2)
Điều kiện tương hợp (liên tục):
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎬
⎫
∂∂
∂
=
∂
∂
+
∂
∂
∂∂
∂
=
∂
∂
+
∂
∂
∂∂
∂
=
∂
∂
+
∂
∂
zx
zx
zy
yz
yx
xy
xzx
z
yz
z
y
xyy
x
γε
ε
γ
ε
ε
γε
ε
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
và
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎬
⎫
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
−
∂
∂
+
∂
∂
∂
∂
=
∂∂
∂
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
−
∂
∂
∂
∂
=
∂∂
∂
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
−
∂
∂
=
∂∂
∂
zyxzyx
zyxyzx
zyxxzy
xy
xz
yz
z
xy
xz
yzy
xy
xz
yz
x
γ
γ
γ
ε
γ
γ
γε
γ
γ
γ
ε
2
2
2
2
2
2
(1.3)
Công thức chuyển của tensor ứng suất. Nếu ký hiệu ma trận các cosin góc giữa hai hệ trục là
[c], tensor ứng suất điểm trong hệ tọa độ Oxyz là [σ], tensor ứng suất trong hệ tọa độ mới [σ∗] tính
theo công thức:
[]
[][ ][]
T
cc
σσ
=
* (1.4)
5
với
[] [ ]
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
zyzxz
yzyxy
xzxyx
zzzyzx
yzyyyx
xzxyxx
ccc
ccc
ccc
c
σττ
τστ
ττσ
σ
;
***
***
***
Ứng suất chính xác định từ phương trình:
⎪
⎭
⎪
⎬
⎫
=−++
=+−+
=++−
0)(
0)(
0)(
mlk
mlk
mlk
zyzxz
zyyxy
zxyxx
σσττ
τσστ
ττσσ
(1.5)
hoặc dưới dạng ma trận:
}0{=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
m
l
k
zzyzx
yzyyx
xzxyx
σσττ
τσστ
ττσσ
(1.6)
trong đó tổng bình phương các cosin bằng đơn vị k2 + l 2 + m2 = 1. Lời giải hệ phương
trình:
σ3 - σ2J1 + σJ2 – J3 = 0. (1.7)
trong đó J1 = σx + σy + σz
J2 = σyσz + σzσx + σxσy - τyx2 - τzx2 - τxy2 (1.8)
J3 = σxσyσz + 2τxyτyzτxz - τxy2σz - τyz2σx - τzx2σy (1.9)
Các đại lượng J1, J2, J3 được gọi bất biến thứ nhất, bất biến thứ hai, và bất biến thứ ba của
tenso ứng suất.
Trường hợp ứng suất phẳng, trong hệ tọa độ xOy ứng suất chính tính theo công thức:
22
4
1
2,1 )(
2xyyx
yx
τσσ
σ
σ
σ
+−±
+
= (1.10)
Hướng trục ứng suất chính tính từ công thức:
yx
xy
n
tg
σσ
τ
θ
−
=2
2 (1.11)
Ứng suất cắt lớn nhất:
2
21
minmax,
σσ
τ
−
±= (1.12)
xy
yx
s
tg
τ
σ
σ
θ
−
=22 (1.13)
Vòng tròn Mohr xây dựng từ phương trình:
6
2
2
2
22 ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−
=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
−yxyx
σσ
τ
σσ
σ
(1.14)
Định luật Hooke áp dụng cho vật liệu đẳng hướng với mô đun đàn hồi E, hệ số Poisson ν.
()
[]
()
[]
()
[]
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
+−=
+−=
+−=
yxzz
zxyy
zyxx
E
E
E
σσνσε
σσνσε
σσνσε
1
1
1
và
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
=
=
=
zxzx
yzyz
xyxy
G
G
G
τγ
τγ
τγ
1
1
1
(1.15)
trong đó )1(2
ν
+
=E
G (1.16)
Nếu ký hiệu: zyx
e
ε
ε
ε
++= có thể viết:
()( )
()( )
()( )
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
+
+
−+
=
+
+
−+
=
+
+
−+
=
zz
yy
xx
E
e
E
E
e
E
E
e
E
ε
ννν
ν
σ
ε
ννν
ν
σ
ε
ννν
ν
σ
1211
1211
1211
(1.17)
⎪
⎭
⎪
⎬
⎫
+=
+=
+=
zz
yy
xx
Ge
Ge
Ge
ελσ
ελσ
ελσ
2
2
2
(1.18)
trong đó
()( )
νν
ν
λ
211 −+
=E mang tên gọi hằng số Lamé.
Hàm ứng suất Airy Φ(x,y) : ∇4Φ(x,y) = 0.
;;;
2
2
2
2
2
yx
yx xyyx ∂∂
Φ∂
−=
∂
Φ∂
=
∂
Φ∂
=
τσσ
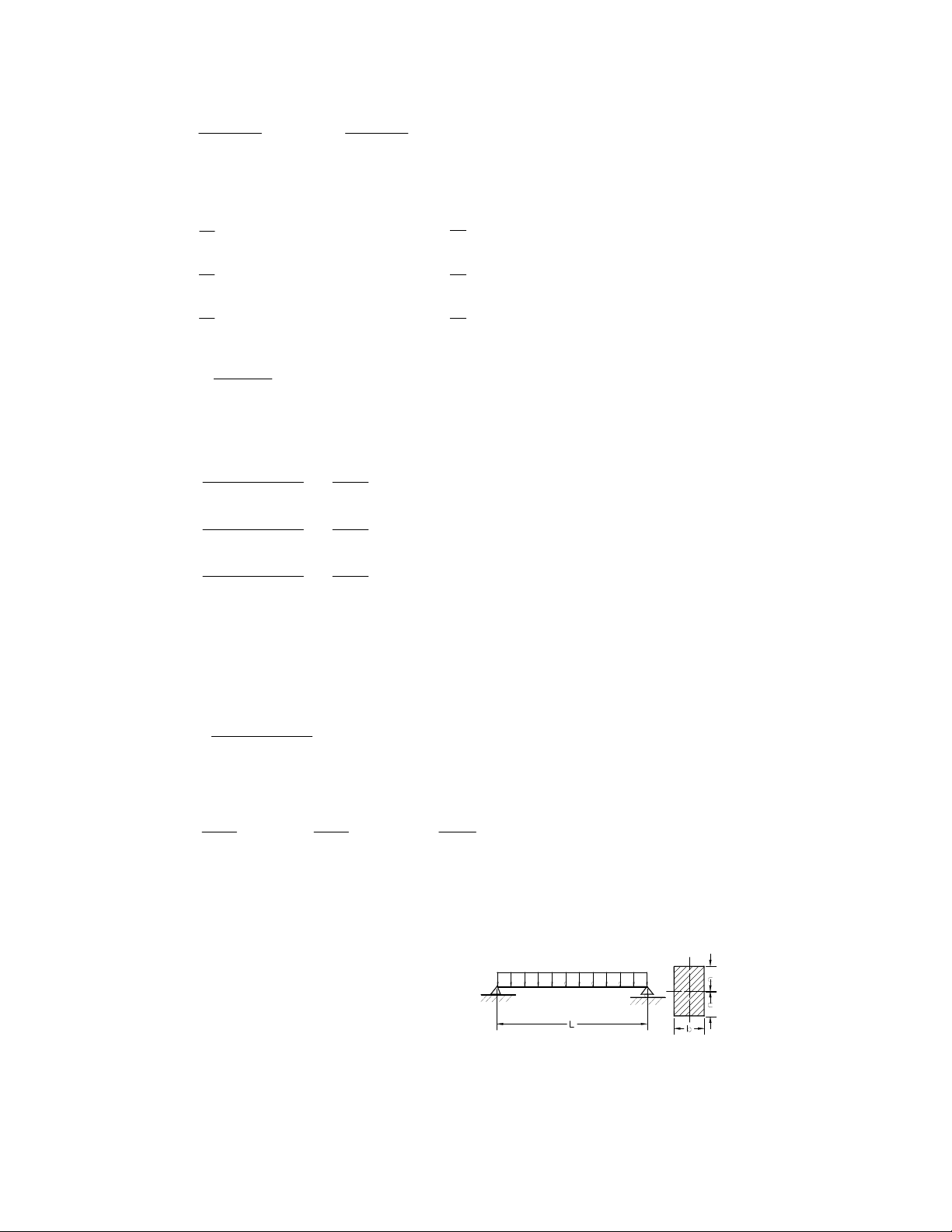
Ví dụ 1: Thành lập hàm ứng suất cho dầm dài L, hình 1.1, mặt cắt ngang hình chữ nhật cạnh đứng 2c,
chiều rộng b, chịu tác động tải phân bố đều q = const.
Điều kiện biên như sau:
a) Tại x = 0:
σx = 0; τxy = 0.
b) Tại x = L:
q
Hình 1.1