zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Tài Liệu Phổ Thông

» Trung học phổ thông

Tài liệu ôn toán - Bài tập hình học lớp 12 - phần 8

Chia sẻ: Nguyễn Ngân | Ngày: | Loại File: PDF | Số trang:10

Báo xấu

164
lượt xem 25
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tham khảo tài liệu 'tài liệu ôn toán - bài tập hình học lớp 12 - phần 8', tài liệu phổ thông, ôn thi đh-cđ phục vụ nhu cầu học tập, nghiên cứu và làm việc hiệu quả

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Tài liệu ôn toán - Bài tập hình học lớp 12 - phần 8

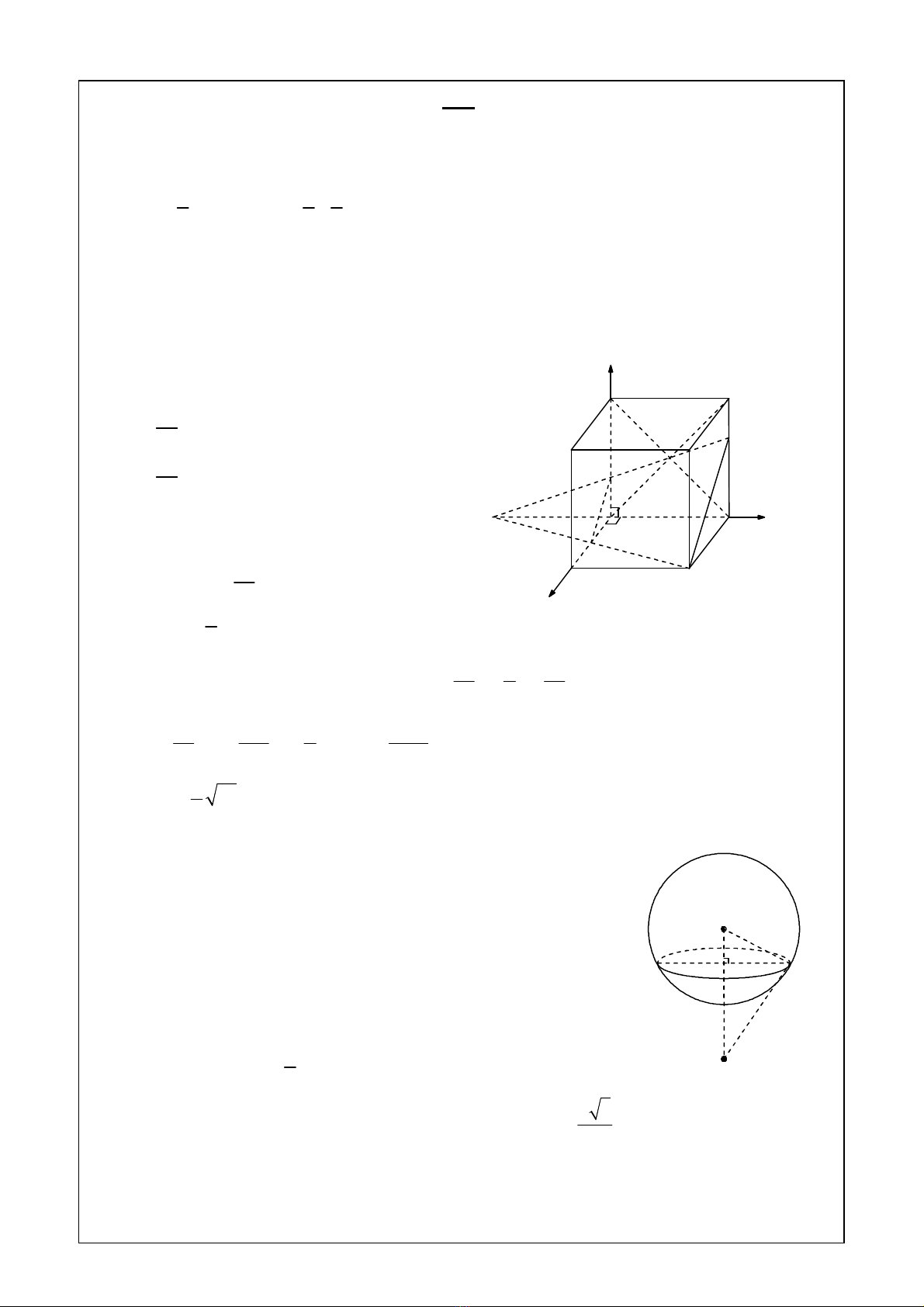
Trần Sĩ Tùng PP Toạ độ trong không gian Giải: Chọn hệ trục tọa độ Axyz sao cho: A(0; 0; 0), B(a; 0; 0), C(a; a; 0), D(0; a; 0) A/(0; 0; a), B/(a; 0; a), C/(a; a; a), D/(0; a; a) æa æ a aö ö Þ M ç ; 0; 0 ÷ , N ç 0; ; ÷ è2 ø è 2 2ø 1. Tính R: Phương trình mặt cầu (S): x 2 + y 2 + z 2 - 2a x - 2 b y - 2g z + d = 0 C , D / , M , N Î (S ) , suy ra: ì2a 2 - 2a a - 2 b a + d = 0 (1) z ï2 ( 2) ï2a - 2b a - 2g a + d = 0 D/ / A ï a2 í -aa + d = 0 (3) L ï4 B/ ï a2 / C K N ( 4) ï - ba -g a + d = 0 î2 D (1) – (2) suy ra: a = g y A (2) – (4) suy ra: d = a2 a M B 5a C (3) Þ a = g = 4 x a (4) Þ b = 4 5a a 5a Þ Phương trình mặt cầu (S): x 2 + y 2 + z2 - x - y - z + a2 = 0 2 2 2 2 2 æ 5a ö æ 5a 2 ö æ a ö 35a 2 2 ÷ + ç ÷ - a2 = R = ç ÷ +ç è 4 ø è 4 ø è 4ø 16 a 35 . Vậy R = 4 2. Tính r: (S) Phương trình mặt cầu (S¢): x 2 + y 2 + z2 - 2a /2 x - 2b / y - 2g / z + d / = 0 A/ , B / , C / , D Î (S / ), suy ra: I ìa2 - 2g / a + d / = 0 R ï2 ïa - 2a / a + d / = 0 (C) C r J í2 / / / / ï3a - 2a a - 2b a - 2g a + d = 0 ï a2 - 2 b / a + d / = 0 î R/ a Þ a / = b / = g / = , d/ = 0 I/ 2 a3 Þ (S / ) : x 2 + y 2 + z2 - ax - ay - az = 0 và bán kính R / = 2 Dễ thấy C(a; a; 0) Î (S / ) Þ C Î (C ) Gọi I , I / , J là tâm của (S), (S/) và (C) Trang 69
PP Toạ độ trong không gian Trần Sĩ Tùng æ 5a a 5a ö / æ a a a ö Þ Iç ; ; ÷, I ç ; ; ÷ è4 4 4ø è2 2 2ø Ta có: JC ^ II / uur uur [II / , CI ] Þ r = d (C, II / ) = II / uur uur uur uur æ a -3a 5a ö a2 / æ 3a a -3a ö / II = ç - ; ÷ ; CI = ç ; ; ÷ Þ [II , CI ] = (-1; 3; 2) è 4 4 4ø è4 4 4ø 4 14 Þr=a 19 3. Tính S: uuur uuu r r a2 n(CMN ) = [CM , CN ] = - (2; - 1; 3) 4 Þ Phương trình mặt phẳng (CMN): 2 x - y + 3z - a = 0 ìx = 0 ï Phương trình đường thẳng AA¢: í y = 0 (t Î R) ïz = t î ìx = 0 ï Phương trình đường thẳng DD¢: í y = a (t Î R) ïz = t î Gọi K = (CMN ) Ç AA/ , L = (CMN ) Ç DD / aö æ 2a ö æ Þ K ç 0; 0; ÷ , L ç 0; a; ÷ è 3ø è 3ø 1 uuur uuu r uuu uuu rr ( ) Þ S = SCMKL = [CM , CK ] + [CK , CL ] 2 1 æ éæ a 2a ö ù ö a öù éæ aö æ öæ = ç êç - ; - a; 0 ÷ , ç - a; - a; ÷ ú + êç - a; - a; ÷ , ç - a; 0; ÷ú ÷ 2 ç ëè 2 3 øû ÷ øè 3 øû ëè 3ø è è ø a 2 14 . ÞS= 4 Trang 70
Trần Sĩ Tùng PP Toạ độ trong không gian BÀI TẬP Baøi 1. Cho tứ diện OABC có đáy OBC là tam giác vuông tại O, OB=a, OC= a 3 , (a>0) và đường cao OA= a 3 . Gọi M là trung điểm của cạnh BC. Tính khoảng cách giữa hai đường thẳng AB và OM. HD: Chọn hệ trục tọa độ sao cho: O(0; 0; 0), A(0; 0; a 3 ), B(a; 0; 0), C (0; a 3; 0) . a 15 Þ d ( AB; OM ) = 5 Baøi 2. Cho hình chóp O.ABC có các cạnh OA = a, OB = b, OC = c đôi một vuông góc. Điểm M cố định thuộc tam giác ABC có khoảng cách lần lượt đến các mp(OBC), mp(OCA), mp(OAB) là 1, 2, 3. Tính a, b, c để thể tích O.ABC nhỏ nhất. HD: Chọn hệ trục tọa độ sao cho: O(0; 0; 0), A(a; 0; 0), B(0; b; 0), C (0; 0; c) . 1231 Þ Vmin = 27 Û === abc3 Baøi 3. Tứ diện S.ABC có cạnh SA vuông góc với đáy và D ABC vuông tại C. Độ dài của các cạnh là SA = 4, AC = 3, BC = 1. Gọi M là trung điểm của cạnh AB, H là điểm đố i xứng của C qua M. Tính cosin góc hợp bởi hai mặt phẳng (SHB) và (SBC). HD: Chọn hệ trục toạ độ sao cho: A(0;0;0), B(1;3;0), C(0;3;0), S(0;0;4) và H(1;0;0). Baøi 4. Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại A, AB = AC = a (a > 0), hình chiếu của S trên đáy trùng với trọng tâm G của DABC. Đặt SG = x (x > 0). Xác định giá trị của x để góc giữa hai mặt phẳng (SAB) và (SAC) bằng 60o. æa a ö æa a ö HD: Chọn hệ trục toạ độ sao cho: A(0;0;0), B(a;0;0), C(0; a; 0), G ç ; ; 0 ÷ , S ç ; ; x ÷ . è3 3 ø è2 2 ø a Þx = . 3 Baøi 5. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy là a. Gọi M, N là trung điểm SB, SC. Tính theo a diện tích DAMN, biết (AMN) vuông góc với (SBC). æa 3 ö HD: Chọn hệ trục toạ độ sao cho: O(0; 0; 0), S(0; 0; h), A ç ; 0; 0 ÷ (SO = h). ç3 ÷ è ø r r 1 uuur uuu r 2 a 2 10 5a Þ SD AMN = é AM , AN ù = Þ ( AMN ) ^ (SBC ) Þ n( AMN ) .n(SBC ) = 0 Þ h 2 = 2ë û 12 16 Baøi 6. Cho lăng trụ ABC.A'B'C' các các mặt bên đều là hình vuông cạnh a. Gọi D, F lần lượt là trung điểm của các cạnh BC, C'B'. Tính khoảng cách giữa hai đường thẳng A'B và B'C'. HD: Chọn hệ trục toạ độ sao cho: æa a 3 ö æ a a 3 ö æa a 3 ö æ aa3 ö A(0; 0; 0), B ç ; ; 0÷, C ç - ; ; 0 ÷ , A '(0; 0; a), B ' ç ; ; a ÷, C 'ç - ; ; a÷ è2 2 ø è2 2 ø è2 2 ø è2 2 ø a 21 Þ d ( A ' B; B ' C ' ) = . 7 Baøi 7. Tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau, AB = 3, AC = AD = 4. Tính khoảng cách từ A tới mặt phẳng (BCD). HD: Chọn hệ trục toạ độ sao cho: A(0;0;0); B(0;0;3); C(0;4;0); D(4;0;0). Baøi 8. Cho hình chóp SABC có độ dài các cạnh đều bằng 1, O là trọng tâm của tam giác DABC. I là trung điểm của SO. a. Mặt phẳng (BIC) cắt SA tại M. Tìm t ỉ số thể tích của tứ diện SBCM và tứ diện SABC. b. H là chân đường vuông góc hạ từ I xuống cạnh SB. Chứng minh rằng IH qua trọng tâm G của DSAC. Trang 71
PP Toạ độ trong không gian Trần Sĩ Tùng æ3 ö æ 31ö æ 31 ö ; 0; 0 ÷ ; B ç - ;- ;0÷ ; C ç - ; ;0÷ ; HD: Chọn hệ trục toạ độ sao cho: O(0; 0; 0), A ç ç3 ÷ ç6 2÷ ç62÷ è ø è ø è ø æ 6ö æ 6ö S ç 0; 0 ÷ ; I ç 0; 0; ÷. ç 3÷ ç 6÷ è øè ø V( SBCM ) 1 Þ = V (SABC ) 4 Baøi 9. Cho hình lăng trụ ABCD. A1B1C1 có đáy là tam giác đều cạnh a. AA1 = 2a và vuông góc với mặt phẳng (ABC). Gọi D là trung điểm của BB1; M di động trên cạnh AA1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của diện tích tam giác MC1D. æa 3 a ö ; ; 2a ÷ , D(0;a;a) HD: Chọn hệ trục toạ độ sao cho: A(0;0;0), B(0;a;0), A1 (0;0;2a), C1 ç ç2 2 ÷ è ø a 2 15 Þ Giá trị lớn nhất SDC M = khi M º A 4 1 Baøi 10. Cho tứ diện SABC có đáy là DABC vuông cân tại B, AB = a, SA ^ ( ABC ) và SA = a. AH ^ SB tại H, AK ^ SC tại K. a. Chứng minh HK ^ SC . b. Gọi I = HK Ç BC. Chứng minh B là trung điểm CI. c. Tính sin góc j giữa SB và (AHK). d. Xác định tâm và bán kính mặt cầu ngoại tiếp SABC. uuur uur a3 2 a/ HK .SC = 0; d/ SJ = JC , R = ; ĐS: c/ 2 6 Baøi 11. Cho tứ diện SABC có đáy là DABC vuông cân tại B, AB = a, SA ^ ( ABC ) và SA = a 2 . Gọi D là trung điểm của AC. a. Chứng minh khoảng cách từ A đến (SBC) gấp đôi khoảng cách từ D đến (SBC). b. Mặt phẳng (a) qua A và vuông góc SC, (a) cắt SC và SB tại M và N. Tính thể t ích hình chóp SAMN. c. Tính cosin của góc tạo bởi hai mặt phẳng (SAC) và (SBC). a3 2 a6 a6 3 ; dB = a/ d A = ĐS: b/ d/ 3 6 18 3 Baøi 12. Cho DABC đều cạnh a. Trên đường thẳng d ^ ( ABC ) tại A lấy điểm S, SA = h. a. Tính d(A, (SBC)) theo a và h. b. Đường thẳng D ^ (SBC ) tại trực tâm H của DSBC, chứng tỏ D luôn qua điểm cố định khi S di động trên d. c. D cắt d tại S/. Tính h theo a để SS/ nhỏ nhất. ah 3 a2 ; d/ a 2 ; h = . b/ Trọng tâm DABC ĐS: a/ 2 3a 2 + 4h 2 Baøi 13. Cho hình chóp S.ABCD đáy là hình vuông cạnh a, SA ^ ( ABCD ) và SA = a 2 . Mặt phẳng (P) qua A và (a ) ^ SC ; (P) cắt các cạnh SB, SC, SD lần lượt tại H, M, K. a. Chứng minh AH ^ SB, AK ^ SD. b. Chứng minh BD // (a) và BD // HK. Trang 72
Trần Sĩ Tùng PP Toạ độ trong không gian c. Chứng minh HK đi qua trọng tâm G của SAC. d. Tính VS.AHMK. uuu r r uuu 3 uuur r uuur uur uuu uuu rr b/ BD.na = 0; BD = HK ; a/ AH .SB = AK .SD = 0 ĐS: 2 a3 2 c/ HG / / GK ; . d/ 18 Baøi 14. Cho hình chóp tứ giác S.ABCD, SA ^ ( ABCD ) và ABCD là hình chữ nhật có AB = a, AD = b, SA = 2a. N là trung điểm SD. a. Tính d(A, (BCN)), d(SB, CN). b. Tính cosin góc giữa hai mặt phẳng (SCD) và (SBC). c. Gọi M là trung điểm SA. Tìm điều kiện a và b để cos· = 1 CMN . 3 Trong trường hợp đó tính VS.BCNM. a3 a2 2ab b ; ; ; c/ a = b; V = . ĐS: a/ b/ 2 4 4a 2 + 5b 2 20a 2 + 5b 2 Baøi 15. Trong mp(P) cho hình vuông ABCD. Trên tia Az ^ (a ) lấy điểm S. Đường thẳng (D1 ) ^ (SBC ) tại S cắt (P) tại M, (D2 ) ^ (SCD ) tại S cắt (P) tại N. Gọi I là trung điểm MN. a. Chứng minh A, B, M thẳng hàng; A, D, N thẳng hàng. b. Khi S di động trên Az, chứng tỏ I thuộc đường thẳng cố định. c. Vẽ AH ^ SI tại H. Chứng minh AH là đường cao tứ diện ASMN và H là trực tâm SMN. d. Cho OS = 2, AB = 1. Tính VASMN. uuur uuu uuu rr uuu r æ h2 h2 ö 2 2 a/ MA = h AB, NA = h AD; b/ I ç - ; - ; 0 ÷ Î AC; ĐS: è2 ø 2 16 c/ AH ^ (SMN ); MN ^ SH ; SM ^ AH ; . d/ 3 Baøi 16. Cho hình chóp S.ABCD có SA ^ ( ABCD ) , đáy ABCD là hình vuông cạnh a. Trên các cạnh BC, CD lấy lần lượt các điểm M, N. Đặt CM = x, CN= y (0 < x, y < a). a. Tìm hệ thức giữa x và y để góc giữa hai mặt phẳng (SAM) và (SAN) bằng 45o. b. Tìm hệ thức giữa x và y để (SAM ) ^ (SMN ) a/ 4a 4 - 4a3 ( x + y ) + 2axy ( x + y ) - x 2 y 2 = 0 b/ x 2 - ax + ay = 0 ĐS: Baøi 17. Cho hình chóp tứ giác đều S.ABCD, cạnh đáy bằng a 2 , đường cao SO, cạnh bên bằng a 5. a. Tính thể tích hình chóp. Xác định tâm I và bán kính R của hình cầu (S) nội tiếp hình chóp. b. Gọi M, N, P lần lượt là trung điểm AB, AD, SC. Mặt phẳng (MNP) cắt SB, SD tại Q và R. Tính diện tích thiết diện. c. Chứng tỏ rằng mặt phẳng (MNP) chia hình chóp ra hai phần có thể tích bằng nhau. 4a3 2a3 a b/ a2 2 ; OI = R = . a/ V = ĐS: c/ 3 2 3 Baøi 18. Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a, đường cao SO. Mặt bên tạo với đáy góc 600 . Mặt phẳng (P) chứa cạnh AB và tạo với đáy góc 300 cắt các cạnh SC, SD lầ n lượt tại M, N. a. Tính góc giữa AN với (ABCD) và BD. Trang 73
PP Toạ độ trong không gian Trần Sĩ Tùng b. Tính khoảng cách giữa AN và BD. c. Tính thể tích hình khố i ABCDMN. 5a3 3 3 3 a/ sin j = . b/ a ĐS: c/ 13 22 48 Baøi 19. Cho hình vuông ABCD cạnh a 2 tâm O. Trên tia Oz ^ ( ABCD ) lấy điểm S, mặt phẳng (SAD) tạo với đáy góc a. a. Xác định và tính độ dài đoạn vuông góc chung của SA và CD. b. Mặt phẳng (b) qua AC và vuông góc (SAD) chia hình chóp thành hai phần. Tính tỉ số thể tích hai phần đó. b/ cos 2 a . a/ a 2 .sin a ĐS: Baøi 20. Cho hình hộp chữ nhật ABCD.A¢B¢C¢D¢ có AB= 2, AD = 4, AA¢ = 6. Gọ i I, J là trung uuuur uuur uuu uuu r r điểm AB, CD¢. Gọi M, N thỏa AM = m AD , BN = mBB / (0 £ m £ 1) a. Tính khoảng cách từ A đến (BDA¢). b. Chứng minh I, M, J, N đồng phẳng. c. Xác định tâm K và bán kính R của mặt cầu (S) ngoại tiếp ABDA¢. d. Tính bán kính r của đường tròn giao của (S) và (BDA¢). uur uu uuu rr 12 5 26 b/ [IN , IJ ].IM = 0 c/ K (1; 2; 3), R = 14; . ĐS: a/ d/ 7 7 Baøi 21. Cho hình lập phương ABCD.A¢B¢C¢D¢ có các cạnh bằng 2. Gọ i M, N là trung điểm AB và DD¢. a. Chứng minh MN // (BDC¢). Tính MN và d(MN, (BDC¢)). b. Gọi P là trung điểm C¢D¢ . Tính VC.MNP và góc giữa MN và BD. c. Tính bán kính R của đường tròn (A/BD). uuuu r r 3 26 b/ V = 1; j = 30o ; a/ MN .n = 0; MN = 6; d = ; . ĐS: c/ 3 3 Baøi 22. Cho lăng trụ OAB.O¢A¢D đáy DOAB vuông tại O, OA= a, OB = b, OO/ = h. Mặt phẳng (P) qua O vuông góc AB¢. a. Tìm điều kiện a, b, h để (a) cắt cạnh AB, AA/ tại I, J (I, J không trùng A, B, A/). b. Với điều kiện trên hãy tính: SDOIJ và tỉ số thể tích 2 phần do thiết diện chia lăng trụ. V1 a 3b a 2 + b 2 + h 2 a4 ; b/ S = a/ a < h = ĐS: V2 3a 2 h 2 + 3b 2 h 2 - a 4 2h(a2 + b 2 ) Baøi 23. Cho tứ diện SABC có ABC là tam giác vuông tại A, SC ^ ( ABC ) và SC = AB = AC = a 2 . Các điểm M thuộc SA và N thuộc BC sao cho AM = CN = t (0 < t < 2a) a. Tính độ dài đoạn MN, tìm t để đoạn MN ngắn nhất. b. Khi MN ngắn nhất, chứng minh rằng MN là đường vuông góc chung của BC và SA. a6 2a a/ MN = 3t 2 - 4at + 2a2 ; min = ,t= b/ MN ^ AM , MN ^ CN . ĐS: 3 3 Baøi 24. Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, có AB= 3, BC = 4. Cạnh bên SA ^ ( ABC ) và SA = 4. a. Tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp SABC. b. Trên AB lấy 1 điểm E với AE = x. Mặt phẳng (P) qua E song song với SA và BC cắt hình chóp theo thiết diện là hình gì? Tính diện tích thiết diện. Tìm x để diện tích này lớn nhất. Trang 74
Trần Sĩ Tùng PP Toạ độ trong không gian 41 3 a/ SI = IC; R = b/ max S = 4, x = . ĐS: 2 2 Baøi 25. Cho tam giác đều SAD và hình vuông ABCD cạnh a nằm trong 2 mặt phẳng vuông góc nhau. Gọi I là trung điểm của AD, M là trung điểm của AB, F là trung điểm của SB. a. Chứng minh rằng mặt phẳng (CMF ) ^ (SIB) . b. Tính khoảng cách giữa 2 đường thẳng AB và SD giữa CM và SA. a3 a3 ; . ĐS: b/ 2 4 Baøi 26. Cho hình lăng trụ đứng ABCD.A¢B¢C¢D¢ có đáy ABCD là hình thoi cạnh a, góc · = 60o . Gọi M là trung điểm cạnh AA¢ và N là trung điểm cạnh CC¢. BAD a. Chứng minh rằng 4 điểm B¢, M, D, N cùng thuộc một mặt phẳng. b. Tính cạnh AA¢ theo a để tứ giác B¢MDN là hình vuông. b/ a 2 . ĐS: Chân thành cảm ơn các bạn đồng nghiệp và các em học sinh đã đọc tập tài liệu này. transitung_tv@yahoo.com Trang 75
Đề thi Tốt nghiệp – Đại học Trần Sĩ Tùng I. KHỐI ĐA DIỆN – KHỐI TRÒN XOAY ĐỀ THI TỐT NGHIỆP Baøi 1. (TN 2006–pb) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, cạnh bên SB bằng a 3 . 1. Tính thể tích của khố i chóp S.ABCD. 2. Chứng minh trung điểm của cạnh SC là tâm mặt cầu ngoại tiếp hình chóp S.ABCD. 1 ĐS: 1) V = a3 2 2) IB = IC = ID = IS. 3 Baøi 2. (TN 2007–pb) Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại đỉnh B, cạnh bên SA vuông góc với đáy. Biết SA = AB = BC = a. Tính thể tích của khố i chóp S.ABC. a3 ĐS: V = . 6 Baøi 3. (TN 2007–pb–lần 2) Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a, cạnh bên SA vuông góc với đáy và SA = AC. Tính thể tích của khố i chóp S.ABCD. a3 2 ĐS: V = . 3 Baøi 4. (TN 2008–pb) Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I là trung điểm của cạnh BC. 1. Chứng minh SA vuông góc với BC. 2. Tính thể tích khố i chóp S.ABI theo a. a3 11 1) BC ^ AI, BC ^ SI Þ BC ^ SA ĐS: 2) V = . 24 Baøi 5. (TN 2008–pb–lần 2) Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B, đường thẳng SA vuông góc với mặt phẳng (ABC). Biết AB = a, BC = a 3 và SA = 3a. 1. Tính thể tích khố i chóp S.ABC theo a. 2. Gọi I là trung điểm của cạnh SC, tính độ dài đoạn thẳng BI theo a. a3 3 a 13 ĐS: 1) V = 2) BI = . 2 2 Baøi 6. (TN 2009) Cho hình chóp S.ABC có mặt bên SBC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Biết · = 120 0 , tính thể tích của khố i chóp S.ABC BAC theo a. a3 2 ĐS: V = . 36 Baøi 7. (TN 2010) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SBD) và mặt phẳng đáy bằng 60 0 . Tính thể tích khố i chóp S.ABCD theo a. a3 6 ĐS: V = . 6 Baøi 8. (TN 2011) ĐS: Trang 76
Trần Sĩ Tùng Đề thi Tốt nghiệp – Đại học ĐỀ THI ĐẠI HỌC Baøi 1. (ĐH 2002A) Cho hình chóp tam giác đều S.ABC đỉnh S, có độ dài cạnh đáy bằng a. Gọi M và N lần lượt là các trung điểm của các cạnh SB và SC. Tính theo a diện tích tam giác AMN, biết rằng mặt phẳng (AMN) vuông góc với mặt phẳng (SBC). a2 10 S= ĐS: 16 Baøi 2. (ĐH 2002B) Cho hình lập phương ABCDA1B1C1D1 có cạnh bằng a. 1. Tính theo a khoảng cách giữa hai đường thẳng A1B và B1D. 2. Gọi M, N, P lần lượt là các trung điểm của các cạnh BB1, CD, A1D1. Tính góc giữa hai đường thẳng MP và C1N. a6 2) MP ^ C1N . ĐS: 1) 6 Baøi 3. (ĐH 2002D) Cho hình tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC); AC = AD = 4cm; AB = 3cm; BC = 5cm. Tính khoảng cách từ điểm A tới mặt phẳng (BCD). 6 34 ĐS: . 17 Baøi 4. (ĐH 2002A–db1) Tính thể t ích khố i tứ diện ABCD, biết AB = 1, AC = b, AD = c và · = · = · = 60 0 . BAC CAD DAB ĐS: Baøi 5. (ĐH 2002A–db2) Cho tam giác vuông cân ABC có cạnh huyền BC = a. Trên đường thẳng vuông góc với mặt phẳng (ABC) tại điểm A lấy điểm S sao cho góc giữa hai mặt phẳng (ABC) và (SBC) bằng 60 0 . Tính độ dài đoạn thẳng SA theo a. ĐS: Baøi 6. (ĐH 2002B–db1) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Gọ i E là trung điểm của cạnh CD. Tính theo a khoảng cách từ điểm S đến đường thẳng BE. ĐS: Baøi 7. (ĐH 2002B–db2) Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc vớ i nhau. Gọ i a, b, g lần lượt là các góc giữa mặt phẳng (ABC) với các mặt phẳng (OBC), (OCA), (OAB). Chứng minh rằng: cos a + cos b + cos g £ 3 . ĐS: Baøi 8. (ĐH 2002D–db1) Cho hình tứ diện đều ABCD, cạnh a = 6 2 . Hãy xác định độ dài đoạn vuông góc chung của hai đường thẳng AD và BC. ĐS: Baøi 9. (ĐH 2002D–db2) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và cạnh bên SA vuông góc với mặt phẳng đáy (ABC). Tính khoảng cách từ điểm A tới mặt phẳng a6 (SBC) theo a, biết rằng SA = . 2 ĐS: Baøi 10. (ĐH 2003A) Cho hình lập phương ABCD.A¢B¢C¢D¢. Tính số đo của góc phẳng nhị diện [B, A¢C, D]. ĐS: 120o Baøi 11. (ĐH 2003B) Cho hình lăng trụ đứng ABCD.A/B/C/D/ có đáy ABCD là một hình thoi cạnh a, góc · = 60o . Gọi M là trung điểm cạnh AA/ và Nlà trung điểm cạnh CC/. BAD Chứng minh rằng bốn điểm B/, M, D, N cùng thuộc một mặt phẳng. Hãy tính độ dài cạnh AA/ theo a để tứ giác B/MDN là hình vuông. Trang 77
Đề thi Tốt nghiệp – Đại học Trần Sĩ Tùng ĐS: a 2 . Baøi 12. (ĐH 2003D) Cho hai mặt phẳng (P) và (Q) vuông góc với nhau, có giao tuyến là đường thẳng D. Trên D lấy hai điểm A, B với AB= a. Trong mặt phẳng (P) lấy điểm C, trong mặt phẳng (Q) lấy điểm D sao cho AC, BD cùng vuông góc với D và AC = BD = AB. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD và tính khoảng cách từ A đến mặt phẳng (BCD) theo a. a3 a2 ; AH = . ĐS: R = 2 2 Baøi 13. (ĐH 2003A–db1) Cho tứ diện ABCD có AB = AC = a, BC = b. Hai mặt phẳng (BCD) và (ABC) vuông góc với nhau và góc · = 90 0 . Xác định tâm và tính bán kính mặt BDC cầu ngoại tiếp tứ diện ABCD theo a và b. ĐS: Baøi 14. (ĐH 2003A–db2) Cho lăng trụ đứng ABC.A¢B¢C¢ có đáy là tam giác cân với AB = AC = a và góc · = 120 0 , cạnh bên BB¢ = a. Gọ i I là trung điểm của CC¢. Chứng minh tam BAC giác AB¢I vuông ở A. Tính cosin của góc giữa hai mặt phẳng (ABC) và (AB¢I). ĐS: Baøi 15. (ĐH 2003B–db1) Cho hình lập phương ABCD.A¢B¢C¢D¢. Tìm điểm M thuộc cạnh AA¢ sao cho mặt phẳng (BD¢M) cắt hình lập phương theo một thiết diện có diện tích nhỏ nhất. ĐS: Baøi 16. (ĐH 2003B–db2) Cho hình chóp đều S.ABC, cạnh đáy bằng a, mặt bên tạo với đáy một góc bằng j (0 0 < j < 90 0 ) . Tính thể t ích khố i chóp S.ABC và khoảng cách từ đỉnh A đến mặt phẳng (SBC). ĐS: Baøi 17. (ĐH 2003D–db1) Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = 2a, cạnh SA vuông góc với đáy và SA = 2a. Gọi M là trung điểm của SC. Chứng minh rằng tam giác AMB cân tại M và tính diện tích tam giác AMB theo a. 22 ĐS: SD AMB = a. 2 Baøi 18. (ĐH 2003D–db2) Cho tứ diện ABCD có AD vuông góc với mặt phẳng (ABC) và tam giác ABC vuông tại A, AD = a, AC = b, AB = c. Tính diện tích S của tam giác BCD theo a, b, c và chứng minh rằng 2S ³ abc(a + b + c) . ĐS: Baøi 19. (ĐH 2004B) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng j ( (00 < j < 900 ) . Tính tang của góc giữa hai mặt phẳng (SAB) và (ABCD) theo j. Tính thể tích khố i chóp S.ABCD theo a và j. a3 2 2 .tan j ; .tan j V= ĐS: 6 Baøi 20. (ĐH 2004B–db1) Cho hình chóp S.ABC có SA = 3a và SA ^ (ABC). Tam giác ABC có AB = BC = 2a, góc · = 1200 . Tính khoảng cách từ điểm A đến mặt phẳng (SBC). ABC ĐS: Baøi 21. (ĐH 2004D–db2) Cho hình vuông ABCD có cạnh AB = a. Trên các nửa đường thẳng Ax, By vuông góc với mặt phẳng (ABCD) và nằm về cùng một phía đố i với mặt phẳng (ABCD), lần lượt lấy các điểm M, N sao cho tam giác MNC vuông tại M. Đặt AM = m, BN = n. Chứng minh rằng m(n - m) = a2 và tìm giá trị nhỏ nhất của diện tích hình thang ABNM. ĐS: Trang 78

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.