intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Tài liệu tự học Toán lớp 11: Hàm số lượng giác và phương trình lượng giác - Trần Quốc Nghĩa

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:107

Thêm vào BST
Báo xấu
21
lượt xem 6
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

"Tài liệu tự học Toán lớp 11: Hàm số lượng giác và phương trình lượng giác - Trần Quốc Nghĩa" gồm 4 phần. Phần 1: Tóm tắt lý thuyết trọng tâm; Phần 2: Các ví dụ mẫu; Phần 3: Các bài tập tự luyện cơ bản; Phần 4: Các câu hỏi trắc nghiệm có đáp án. Mời thầy cô và các em cùng tham khảo.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Tài liệu tự học Toán lớp 11: Hàm số lượng giác và phương trình lượng giác - Trần Quốc Nghĩa

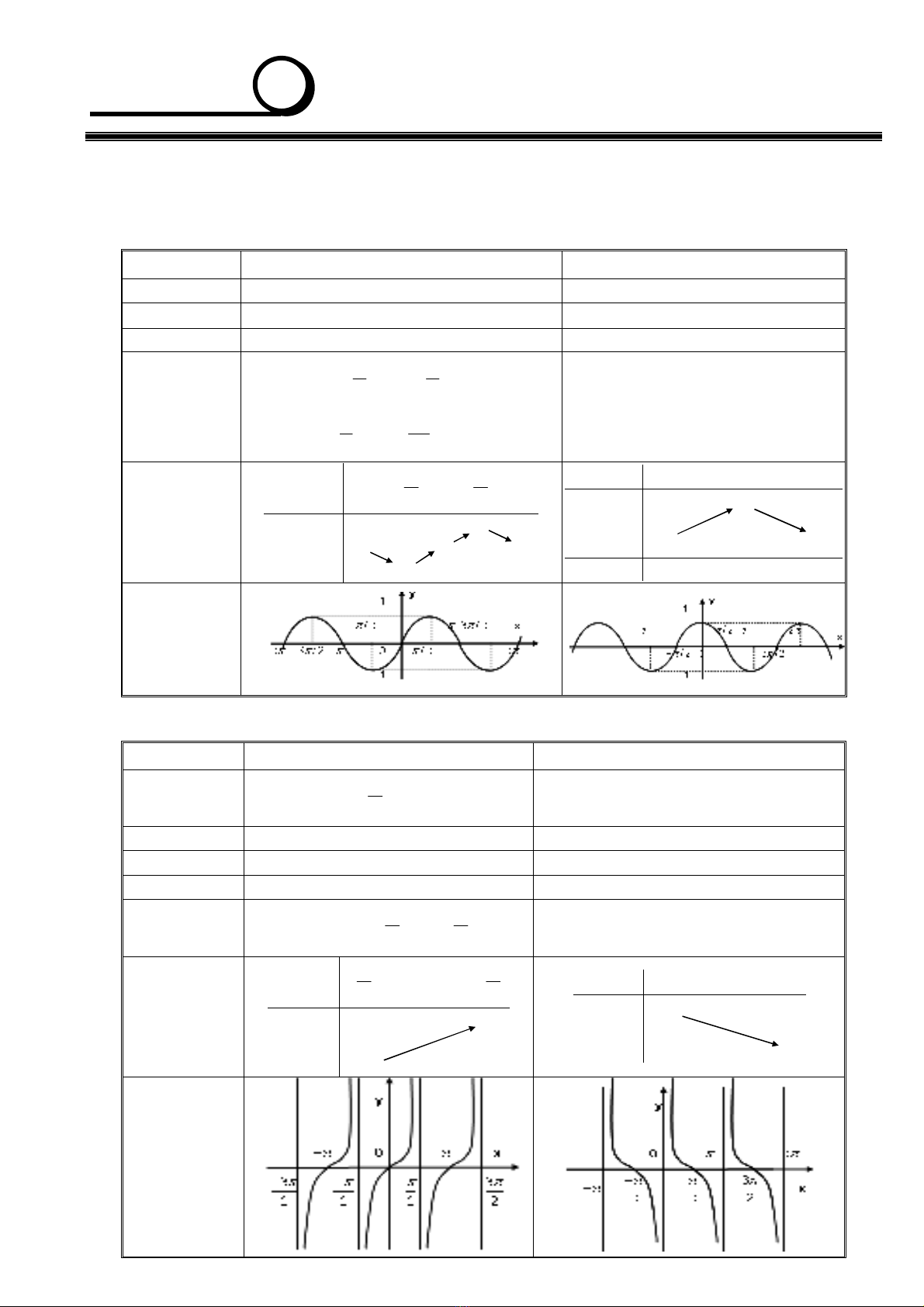
  1. GV. TRẦN QUỐ QUỐC NGHĨA NGHĨA (Sưu (Sưu tầ tầm và Biên tậ tập) 1 Ll20202020v ,. Chuyênđề 1 LƯỢNG GIÁC Phần 1 - HÀM SỐ LƯỢNG GIÁC 1. Hàm số y = sin x và y = cos x y = sin x y = cos x Tập xác định D=ℝ D=ℝ Chu kỳ T = 2π T = 2π Tính chẵn lẻ Lẻ Chẵn  π π  HSĐB trên:  − + k2π ; + k2π   2 2  HSĐB trên: ( −π + k 2π ; k 2π ) Sự biến thiên π 3π  HSĐB trên: ( k 2π ; π + k 2π ) HSNB trên:  + k2π ; + k2π  2 2  π π x –π 0 π x –π − 0 π Bảng biến 2 2 1 1 y = cos x thiên y = sin x 0 0 0 –1 –1 –1 Đồ thị 2. Hàm số y = tan x và y = cot x y = tan x y = cot x π  Tập xác định D = ℝ \  + kπ , k ∈ ℤ  D = ℝ \ {kπ , k ∈ ℤ} 2  Tập giá trị ℝ ℝ Chu kỳ T =π T =π Tính chẵn lẻ Lẻ Lẻ  π π  Nghịch biến trên mỗi khoảng: Sự biến thiên Đồng biến trên  − + kπ ; + kπ   2 2  ( kπ ; π + kπ ) π π x − x 0 π Bảng biến 2 2 +∞ thiên +∞ y = cot x y = tan x –∞ –∞ Đồ thị
  2. TÀI LIỆ LIỆU HỌ HỌC TẬ TẬP TOÁN 11 – CHỦ CHỦ ĐỀ 1: LƯ LƯỢNG GIÁC 2 Dạng 1. Tìm tập xác định của hàm số A. PHƯƠNG PHÁP GIẢI Tập xác định của hàm số y = f ( x ) là tập hợp tất cả các giá trị của biến số x sao cho f(x) có nghĩa. f ( x) • y= có nghĩa ⇔ g ( x) ≠ 0 g ( x) • y = 2 n f ( x ) có nghĩa ⇔ f ( x ) ≥ 0, (n ∈ ℕ) • y = 2 n +1 f ( x) có nghĩa ⇔ f ( x ) có nghĩa (n ∈ ℕ) π • y = tan f ( x ) có nghĩa ⇔ cos f ( x ) ≠ 0 ⇔ f ( x ) ≠ + kπ ,( k ∈ℤ ) 2 • y = cot f ( x) có nghĩa ⇔ sin f ( x ) ≠ 0 ⇔ f ( x ) ≠ kπ ,(k ∈ ℤ) B. BÀI TẬP MẪU Ví dụ 1. Tìm tập xác định của mỗi hàm số sau: 1 − cos x 1 − sin x  π  π a) y = b) y = c) y = tan  x −  d) y = cot  x +  sin x 1 + cos x  3  6 ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. .................................................................................................................................................................................
  3. GV. TRẦN QUỐ QUỐC NGHĨA NGHĨA (Sưu (Sưu tầ tầm và Biên tậ tập) 3 C. BÀI TẬP CƠ BẢN Bài 1. Tìm tập xác định của mỗ i hàm số sau: x 3 2x a) y = sin 3x b) y = cos c) y = d) y = cos 2 2 cos x x −1  π  π e) y = 3 − sin x f) y = tan  2 x +  g) y = cos x h) y = cot  2 x −   3  4 D. BÀI TẬP NÂNG CAO Bài 2. Tìm tập xác định của mỗ i hàm số sau: 1+ x sin x + 2 cot x x a) y = sin b) y = c) y = d) y = tan 1− x cos x + 1 cos x − 1 3 1 2 3 e) y = sin 2 f) y = g) y = tan x + cot x h) y = x −1 cos x − cos 3x sin x − cos 2 x 2 Bài 3. Tìm m để hàm số sau xác định ∀x ∈ ℝ : y = sin 4 x + cos4 x − 2m sin x cos x Bài 4. Tìm tập xác định của các hàm số: a) y = 2 + tan 2 x − cos x b) y = sin 2 x − sin x + 3 Dạng 2. Tìm giá trị lớn nhất. Giá trị nhỏ nhất của hàm số lượng giác A. PHƯƠNG PHÁP GIẢI • Sử dụng phương pháp miền giá trị của hàm số lượng giác. ∀x ∈ ℝ : 2 2  −1 ≤ sin x ≤ 1 , −1 ≤ cos x ≤ 1  0 ≤ sin x ≤ 1 , 0 ≤ cos x ≤ 1  0 ≤ sin x ≤ 1 , 0 ≤ cos x ≤ 1  0 ≤ sin x ≤ 1 , 0 ≤ cos x ≤ 1 (khi sin x ≥ 0 , cos x ≥ 0 ) • Sử dụng các tính chất của bắt đẳng thức: a ≤ b  a≤b⇔b≥a  b ≤ c ⇔ a ≤ c  a ≤ b  a ≤ b ⇔ a + c ≤ b + c (cộng 2 vế với c)  c ≤ d ⇔ a + c ≤ b + d   a ≤ b ⇔ a.c ≤ b.c (nếu c > 0: giữ nguyên chiều) a ≤ b ⇔ a.c ≥ b.c (nếu c < 0: đổi chiều) a > b > 0 1 1  c > d > 0 ⇔ a.c > b.d  a>b>0⇔ a < b  2 n +1 2n 2n *  a > b > 0 ⇔ a > b (n ∈ ℕ )  a>b⇔a > b 2 n +1 ( n ∈ ℕ* ) • Sử dụng các bất đẳng thức quen thuộc: Cô-si, BCS, … B. BÀI TẬP MẪU Ví dụ 2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗ i hàm số sau:  π a) y = 2 cos x + 1 b) y = 3 – 2sin x c) y = 2cos  x +  + 3 d) y = 1 − sin( x 2 ) − 1  3 ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................
  4. TÀI LIỆ LIỆU HỌ HỌC TẬ TẬP TOÁN 11 – CHỦ CHỦ ĐỀ 1: LƯ LƯỢNG GIÁC 4 ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. C. BÀI TẬP CƠ BẢN Bài 5. Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗ i hàm số sau: 1 + 4cos2 x a) y = b) y = 4sin x c) y = 2(1 + cos x ) + 1 3 d) y = cos2 x + 2cos 2 x e) y = 2 + 3cos x f) y = 3 – 4sin 2 x cos2 x g) y = 2sin 2 x – cos 2 x h) y = 3 – 2 sin x i) y = 3 – 4sin x  π  π j) y = 3sin  x −  − 2 k) y = 5 − 2cos2 x sin 2 x l) y = cos x + cos  x −   6  3 D. BÀI TẬP NÂNG CAO Bài 6. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số a) y = sin x + cos x b) y = sin x (1 − 2 cos 2 x ) Bài 7. Tìm giá trị lớn nhất của hàm số y = cot 4 x + cot 4 y + 2 tan 2 x tan 2 y + 2 . Bài 8. Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau  π 2π  a) y = sin x trên đoạn  − ;  .  3 3   π  π  π π b) y = cos  2 x +  − cos  2 x −  trên đoạn  − ;  .  4  4  3 6 Dạng 3. Xét tính chẵn – lẻ của hàm số A. PHƯƠNG PHÁP GIẢI Cho hàm số y = f ( x ) xác định trên D : ∀x ∈ D ⇒ − x ∈ D a) Hàm số chẵn trên D nếu   f (− x ) = f ( x ) ∀x ∈ D ⇒ − x ∈ D b) Hàm số lẻ trên D nếu   f (− x ) = − f ( x )  ∀x ∈ D ⇒ − x0 ∉ D c) Hàm số không chẵn, không lẻ trên D nếu:  0  ∀x0 ∈ D : f (− x0 ) ≠ f ( x0 ) ≠ − f ( x0 )  Nhận xét:  Hàm số chẵn có đồ thị đối xứng qua trục tung  Hàm số lẻ có đồ thị đối xứng qua gốc tọa độ.  Chú ý:  x = −x  (a − b) 2 n = (b − a) 2 n , n ∈ ℝ  (a − b) 2 n +1 = −(b − a) 2 n +1 , n ∈ ℝ
  5. GV. TRẦN QUỐ QUỐC NGHĨA NGHĨA (Sưu (Sưu tầ tầm và Biên tậ tập) 5 B. BÀI TẬP MẪU Ví dụ 3. Xét tính chẵn lẻ của mỗ i hàm sồ sau: a) y = x – sin x b) y = 3sin x – 2 c) y = sin x – cos x cos x d) y = sin x cos x + tan x e) y = f) y = 1 − cos x x ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................
  6. TÀI LIỆ LIỆU HỌ HỌC TẬ TẬP TOÁN 11 – CHỦ CHỦ ĐỀ 1: LƯ LƯỢNG GIÁC 6 C. BÀI TẬP CƠ BẢN VÀ NÂNG CAO Bài 9. Xét tính chẵn lẻ của mỗ i hàm sồ sau: tan x + cot x 1 + cos x a) y = b) y = c) y = x 3 sin 2 x 1 − sin 2 x 1 − cos x  π x3 − sin x d) y = cos3 x e) y = tan  x +  f) y =  5 cos 2 x x sin 4 1 − x 2 − cos 6 x 2 − 1 g) y = h) y = sin x + tan x 1− x Dạng 4. Tính tuần hoàn của hàm số A. PHƯƠNG PHÁP GIẢI Để xét tính tuần hoàn của các hàm số ta dựa vào khái niệm sau: Hàm số y = f ( x ) xác định trên tập D được gọi là hàm số tuần hoàn nếu ∀x ∈ D ⇒ x ± T ∈ D ∃T ≠ 0 sao cho  .  f ( x + T ) = f ( x ) , ∀x ∈ D Nếu tồn tại số T > 0 nhỏ nhất thỏa mãn các điều kiện trên thì T được gọi là chu kỳ của hàm số tuần hoàn y = f ( x ) . 2π 2π Chú ý: ● y = sin ( ax + b ) có chu kỳ T0 = . ● y = cos ( ax + b ) có chu kỳ T0 = . a a π π ● y = tan ( ax + b ) có chu kỳ T0 = . ● y = cot ( ax + b ) có chu kỳ T0 = . a a ● y = f1 ( x ) có chu kỳ T1 và y = f 2 ( x ) có chu kỳ T2 thì hàm số y = f1 ( x ) ± f 2 ( x ) có chu kỳ T0 là bội chung nhỏ nhất của T1 và T2 . C. BÀI TẬP MẪU Ví dụ 4. Xét tính tuần hoàn và tìm chu kỳ của các hàm số sau 1 a) y = 1 + sin 2 2 x . b) y = . sin 2 x ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. .................................................................................................................................................................................
  7. GV. TRẦN QUỐ QUỐC NGHĨA NGHĨA (Sưu (Sưu tầ tầm và Biên tậ tập) 7 ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ Ví dụ 5. Xét tính tuần hoàn và tìm chu kỳ của các hàm số sau a) y = x + sin x . b) y = sin 2 2 x + cos 2 2 x . ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ C. BÀI TẬP CƠ BẢN VÀ NÂNG CAO Bài 10. Xét tính tuần hoàn và tìm chu kỳ của các hàm số sau ( a ≠ 0 ): a) y = sin ( ax + b ) b) y = cos ( ax + b ) c) y = tan ( ax + b ) d) y = cot ( ax + b ) Bài 11. Xét tính tuần hoàn và tìm chu kỳ của các hàm số: a) y = cos3x. (1 + cos x ) b) y = sin 6 x + cos6 x c) y = sin( x 2 )
  8. TÀI LIỆ LIỆU HỌ HỌC TẬ TẬP TOÁN 11 – CHỦ CHỦ ĐỀ 1: LƯ LƯỢNG GIÁC 8 Dạng 5. Sử dụng đồ thị A. PHƯƠNG PHÁP GIẢI • Vẽ đồ thị hàm số trên miền đã chỉ ra. • Dựa vào đồ thị xác định giá tị cần tìm. B. BÀI TẬP MẪU  3π  Ví dụ 6. Hãy xác định giá trị của x trên đoạn  −π ; để hàm số y = tan x nhận giá trị:  2  a) bằng 0 . b) bằng 1 . c) dương. d) âm. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. .................................................................................................................................................................................  3π  Ví dụ 7. Dựa vào đồ thị hàm số y = sin x , tìm những giá trị của x trên đoạn  − ; 2π  để hàm số đó:  2  a) Nhận giá trị bằng –1 . b) Nhận giá trị âm. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. .................................................................................................................................................................................
  9. GV. TRẦN QUỐ QUỐC NGHĨA NGHĨA (Sưu (Sưu tầ tầm và Biên tậ tập) 9 B. BÀI TẬP CƠ BẢN VÀ NÂNG CAO 1 Bài 12. Dựa vào đồ thị hàm số y = cos x , tìm các giá trị của x để cos x = . 2 Bài 13. Cho các hàm số f ( x ) = sin x , g ( x ) = cos x , h ( x ) = tan x và các khoảng:  3π   π π  31π 33π   452π 610π  J1 =  π ;  , J 2 =  − ;  , J3 =  ;  , J4 =  − ;−   2   4 4  4 4   3 4  Hỏi hàm nào trong ba hàm trên đồng biến trên khoảng J1 ? Trên khoảng J 2 ? Trên khoảng J 3 ? Trên khoảng J 4 ? (Trả lời bằng cách lập bảng biến thiên) Bài 14. Trong mỗi khẳng định sau, khẳng định nào đúng? Khẳng định nào sai? Giải thích vì sao? a) Trên mỗ i khoảng mà hàm số y = sin x đồng biến thì hàm số y = cos x nghịch biến. b) Trên mỗ i khoảng mà hàm số y = sin 2 x đồng biến thì hàm số y = cos2 x nghịch biến. Bài 15. Dựa vào đồ thị hàm số y = sin x hãy vẽ đồ thị hàm số y = sin x . Bài 16. Cho hàm số y = f ( x ) = 2 sin 2 x a) Chứng minh rằng với số nguyên dương k tùy ý, luôn có f ( x + kπ ) = f ( x ) với mọ i x .  π π b) Lập bảng biến thiên của hàm số y = 2sin 2 x trên đoạn  − ;  .  2 2 c) Vẽ đồ thị của hàm số y = 2sin 2 x Bài 17. CMR: sin 2( x + kπ ) = sin 2 x với mọ i số nguyên k . Từ đó vẽ đồ thị hàm số y = sin 2 x . 1 x x Bài 18. CMR: cos ( x + k 4π ) = cos với mọ i số nguyên k . Từ đó vẽ đồ thị hàm số y = cos rồi suy 2 2 2 x ra đồ thị hàm số y = cos . 2
  10. TÀI LIỆ LIỆU HỌ HỌC TẬ TẬP TOÁN 11 – CHỦ CHỦ ĐỀ 1: LƯ LƯỢNG GIÁC 10 Phần 2 - PHƯƠNG TRÌNH LƯỢNG GIÁC Dạng 1. Phương trình cơ bản A. PHƯƠNG PHÁP GIẢI  Chú ý:  Khi gặp dấu trừ ở trước thì: – sin x = sin ( – x ) – cos x = cos (π – x ) – tan x = tan ( – x ) – cot x = cot ( – x ) 0  Khi giải phải dùng đơn vị là rad nếu đề bài không cho độ ( ).
  11. GV. TRẦN QUỐ QUỐC NGHĨA NGHĨA (Sưu (Sưu tầ tầm và Biên tậ tập) 11 B. BÀI TẬP MẪU Ví dụ 8. Giải các phương trình sau: 3  π 2 a) sin x = − b) cos  3 x −  = − c) tan ( 3 x – 30° ) = –1 2  6 2  π 3 1 1 d) cot  x +  = e) sin x = f) cos ( x + 3) =  3 3 4 3 ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................
  12. TÀI LIỆ LIỆU HỌ HỌC TẬ TẬP TOÁN 11 – CHỦ CHỦ ĐỀ 1: LƯ LƯỢNG GIÁC 12 C. BÀI TẬP CƠ BẢN Bài 19. Giải các phương trình sau: 1 2 a) sin ( x – 60° ) = b) sin 2 x = –1 c) cos ( x – 2 ) = 2 5  π 1 1  π d) cos  2 x +  = − e) cos ( 2 x + 50° ) = f) cot  4 x −  = 3  3 2 2  6 x π π x  3 2π g) tan  −  = tan h) cot  + 20°  = − i) tan 2 x = tan 2 4 8 3  3 7 2 3 3 j) sin 4 x = k) cos ( 3x – 45° ) = l) sin 3x = – 3 2 2 3 x  1 3 m) sin ( 2 x –15° ) = − n) sin  + 10°  = − o) sin 2 x = 2 2  2 2 Dạng 2. Phương trình bậc nhất theo một hàm số lượng giác A. PHƯƠNG PHÁP GIẢI  Phương trình bậc nhất theo một hàm số lượng giác là các phương trình có dạng: asinx + b = 0 ; acosx + b = 0 ; atanx + b = 0 ; acotx + b = 0  Phương pháp giải: Chuyển về phương trình lượng giác cơ bản. B. BÀI TẬP MẪU Ví dụ 9. Giải các phương trình sau:  π a) 3sin 4 x = 2 b) 2sin 2 x − 1 = 0 c) 3 cot  x +  − 1 = 0  3 d) 2cos ( x + 50° ) = − 3 e) 2cos x – 3 = 0 f) 3 tan 3x – 3 = 0 ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. .................................................................................................................................................................................
  13. GV. TRẦN QUỐ QUỐC NGHĨA NGHĨA (Sưu (Sưu tầ tầm và Biên tậ tập) 13 Ví dụ 10. Giải các phương trình sau:  π  x  x  a) cos 2 x.cot  x −  = 0 b)  cot − 1 cot + 1 = 0  4  3  2  c) (1 + 2 cos x )( 3 – cos x ) = 0 d) ( cot x + 1) .sin 3 x = 0 ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ Ví dụ 11. Giải các phương trình sau: a) cos 3x – sin 2 x = 0 b) tan x. tan 2 x = –1 ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................
  14. TÀI LIỆ LIỆU HỌ HỌC TẬ TẬP TOÁN 11 – CHỦ CHỦ ĐỀ 1: LƯ LƯỢNG GIÁC 14 C. BÀI TẬP CƠ BẢN Bài 20. Giải các phương trình sau: a) sin 2 x.cot x = 0 b) tan ( x – 30° ) .cos ( 2 x –150° ) = 0 c) ( 2cos 2 x –1) (2sin 2 x – 3 ) = 0 ( ) d) 3tan x + 3 ( 2sin x –1) = 0 e) tan ( 2 x + 60° ) cos ( x + 75° ) = 0 f) ( 2 + cos x )( 3cos 2 x – 1) = 0 ( g) ( sin x + 1) 2cos 2 x – 2 = 0 ) h) ( sin 2 x – 1)( cos x + 1) = 0 C. BÀI TẬP NÂNG CAO Bài 21. Giải các phương trình sau: a) sin 3x = cos 2 x b) cos x = – sin 2 x c) sin 3x + sin 5 x = 0 d) cot 2 x.cot 3x = 1 e) sin x – cos ( x + 60° ) = 0 f) cos ( x –10° ) + sin x = 0  π  π  π g) sin  x +  = − sin  2 x −  h) cos  2 x −  = − cos x  3  4  4 i) tan 3 x + tan x = 0 f) tan 3 x + tan ( 2 x – 45° ) = 0 k) sin 2 x + cos 3x = 0 l) tan x.tan 3 x = 1 m) cot 2 x cot ( x + 45° ) = 1 n) tan ( 3 x + 2 ) + cot 2 x = 0  π π   π  π o) cos  2 x −  − sin  − x  = 0 p) cos  2 x +  + cos  x −   4 3   3  6 ( q) ( sin x + 1) 2cos 2 x – 2 = 0 ) r) ( sin 2 x – 1)( cos x + 1) = 0 Bài 22. Giải các phương trình sau: 1 a) sin 2 x = b) 4cos 2 x – 3 = 0 c) sin 2 3 x – cos 2 x = 0 4 d) sin ( x – 45° ) = cos 2 x 2 e) 8cos3 x –1 = 0 f) tan 2 ( x + 1) = 3 Dạng 3. Tìm nghiệm phương trình lượng giác trên khoảng, đoạn cho trước A. PHƯƠNG PHÁP GIẢI  Bước 1. Giải phương trình lượng giác đã cho và tìm các họ nghiệm (nếu có)  Bước 2. Với mỗi họ nghiệm tìm được, cho thuộc khoảng, đoạn đề cho và tìm k (k ∈ℤ)  Bước 3. Ứng với mỗi giá trị k vừa tìm được, thế vào họ nghiệm tìm nghiệm tương ứng. B. BÀI TẬP MẪU Ví dụ 12. Giải các phương trình sau: 2  π 3 a) sin ( 2 x –15° ) = với –120° < x < 90° b) tan  2 x +  = − với 0 < x < π 2  4 3 ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. .................................................................................................................................................................................
  15. GV. TRẦN QUỐ QUỐC NGHĨA NGHĨA (Sưu (Sưu tầ tầm và Biên tậ tập) 15 ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ C. BÀI TẬP CƠ BẢN Bài 23. Giải các phương trình sau: 1  π 1 a) cos ( 2 x + 10 ) = với –π < x < π b) sin  2 x −  = − với 0 < x < 2π 2  3 2 1 2 c) sin x = – với –π < x < 0 d) cos ( x – 2 ) = với x ∈ [0; π ] 2 2  π e) tan ( x – 10° ) = 1 với –15° < x < 15° f) sin  x +  = 1 với x ∈ [π ; 2π ]  4 C. BÀI TẬP NÂNG CAO Bài 24. Tìm nghiệm thuộc đoạn [ 0;14] của phương trình: cos 3x − 4 cos 2 x + 3cos x − 4 = 0  π  sin 2 x − cos 2 x Bài 25. Tính giá trị của x ∈  − ; 0  thỏa mãn phương trình: cot x =  2  2 + sin 2 x  cos 3x + sin 3 x  Bài 26. Tìm nghiệm thuộc ( 0; 2π ) của phương trình: 5  sin x +  = cos 2 x + 3  1 + 2sin 2 x 
  16. TÀI LIỆ LIỆU HỌ HỌC TẬ TẬP TOÁN 11 – CHỦ CHỦ ĐỀ 1: LƯ LƯỢNG GIÁC 16 Dạng 4. Phương trình bậc hai, bậc 3 đối với một hàm số lượng giác A. PHƯƠNG PHÁP GIẢI  Là các phương trình mà sau khi biến đổi ta được một trong các dạng sau ( a ≠ 0 ) : • asin 2 u + bsinu + c = 0 ( 1) • acos 2 u + bcosu + c = 0 ( 1) Đặt t = sinu Đặt t = cosu Điều kiện: –1 ≤ t ≤ 1 Điều kiện: –1 ≤ t ≤ 1 (1) ⇔ at 2 + bt + c = 0 (1) ⇔ at 2 + bt + c = 0 • a tan 2 u + b tan u + c = 0 ( 1) • acot 2 u + bcotu + c = 0 ( 1) Điều kiện: cos u ≠ 0 . Điều kiện: sinu ≠ 0 Đặt t = tanu , Đặt t = cotu , (1) ⇔ at 2 + bt + c = 0 (1) ⇔ at 2 + bt + c = 0 B. BÀI TẬP MẪU Ví dụ 13. Giải các phương trình sau: a) 2sin 2 x + 3sin x − 2 = 0 b) 3cot 2 x + 3cot x − 2 = 0 c) 3cos 2 x − 5cos x + 2 = 0 d) 3 tan 2 x − 2 3 tan x + 1 = 0 ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. .................................................................................................................................................................................
  17. GV. TRẦN QUỐ QUỐC NGHĨA NGHĨA (Sưu (Sưu tầ tầm và Biên tậ tập) 17 Ví dụ 14. Giải các phương trình sau: a) tan 3 x – 3tan 2 x – 2 tan x + 4 = 0 b) 4sin 3 x + 4sin 2 x – 3sin x = 3 ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ ................................................................................................................................................................................ C. BÀI TẬP CƠ BẢN Bài 27. Giải các phương trình sau: a) 2cos 2 x + 2 cos x – 2 = 0 b) 2cos 2 x – 3cos x + 1 = 0 c) 6sin 2 x – 5sin x – 4 = 0 ( ) d) 3 tan 2 x − 1 + 3 tan x + 1 = 0 x x ( ) e) tan 2 3 x + 1 − 3 tan 3x − 3 = 0 f) 4cot 2 − 2( 3 − 1) cot − 3=0 3 3 x x x x g) 4cos 2 2 ( − 2 2 + 1 cos + 2 = 0 2 ) h) 2sin 2 2 + 2 sin − 2 = 0 2 2 2 i) 2sin x − 3sin x − 5 = 0 j) 2 tan x + 3tan x + 1 = 0 Bài 28. Giải các phương trình sau: a) sin 2 x – 2cos x + 2 = 0 b) cos2 x + sin x + 1 = 0 c) 2cos 2 x + 4sin x + 1 = 0 d) 2cos 2 x – 2 ( ) 3 + 1 cos x + 3 + 2 = 0 e) cos 2 x + 9 cos x + 5 = 0 f) cos5 x.cos x = cos 4 x.cos 2 x + 3cos 2 x + 1  π π  5 g) cot 4 x – 4cot 2 x + 3 = 0 h) cos 2  x +  + 4cos  − x  =  3 6  2 4 1 i) tan 2 x – +5 = 0 j) – 1 + tan x – 3 ( tan x + 1) = 0 cos x cos 2 x 1 − tan 2 x k) tan x − 2 cot x + 1 = 0 l) cos 4 x – 3 +2=0 1 + tan 2 x C. BÀI TẬP NÂNG CAO Bài 29. Giải các phương trình sau:  π  π 9 a) sin 4 x + sin 4  x +  + cos 4  x +  =  4  4 8  π  π b) cos  2 x +  + cos  2 x −  + 4sin x = 2 + 2 (1 − sin x )  4  4 Bài 30. Giải các phương trình sau: 1 π  a) tan 3 x –1 + 2 + 2cot  − x  = 3 b) 2sin 2 x = 1 + sin 3 x cos x 3  c) 1 + sin 3x = sin x + cos 2 x d) tan 2 x + cot 2 x + 2 ( tan x + cot x ) = 6 1 1 7 1 5 e) cos 2 x + 2 + cos x − − =0 f) 2 + cot 2 x + ( tan x + cot x ) + 2 = 0 cos x cos x 4 cos x 2
  18. TÀI LIỆ LIỆU HỌ HỌC TẬ TẬP TOÁN 11 – CHỦ CHỦ ĐỀ 1: LƯ LƯỢNG GIÁC 18 Dạng 5. Phương trình bậc nhất đối với sin x và cos x (Phương trình cổ điển) A. PHƯƠNG PHÁP GIẢI a sin x + b cos x = c (1) với a, b, c ∈ ℝ , và a 2 + b 2 ≠ 0 Điều kiện để phương trình có nghiệm là: a 2 + b 2 ≥ c 2 Chia 2 vế phương trình cho a 2 + b 2 , ta được: a b c .s inx + .cos x = a 2 + b2 a 2 + b2 a 2 + b2 2 2  a   b  a b Vì  2 2  + 2 2  = 1 nên đặt cos α = 2 2 , sin α =  a +b   a +b  a +b a + b2 2 c Khi đó ta được: sin ( x + α ) = rồi giải như phương trình cơ bản. a + b2 2  Chú ý: Nếu a = b có thể dùng công thức sau để giải:  π  π sin x ± cos x = 2 sin  x ±  = ± 2 cos  x ∓   4  4 B. BÀI TẬP MẪU Ví dụ 15. Giải các phương trình sau: a) sin x + 3 cos x = 1 b) cos x – 3 sin x = 2 c) 3sin 3 x – 4cos 3x = 5 d) 2sin x + 2cos x − 2 = 0 ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. ................................................................................................................................................................................. .................................................................................................................................................................................
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
6=>0