TOÁN HỌC RỜI RẠC
PHẦN 1
DISCRETE MATHEMATICS
PART ONE
NỘI DUNG ÔN TẬP
PHẦN 1
1. CƠ SỞ LOGIC
a. Phép tính mệnh đề & vị từ
b. Quy tắc suy luận. Quy nạp
2. ĐẠI SỐ BOOL
a. Quan hệ thứ tự & tập hợp được sắp
b. Dàn và đại số bool
c. Hàm bool
d. Phương trình bool & hệ phủ tối tiểu
e. Công thức tối tiểu của hàm bool
PHẦN 2
1. PHÉP ĐẾM
a. Nguyên lý cộng, nhân & bù trừ
b. Giải tích tổ hợp
c. Nguyên lý Dirichlet
d. Công thức đệ quy
2
NỘI DUNG ÔN TẬP (cont.)
2. LÝ THUYẾT ĐỒ THỊ
a. Đại cương
b. Đồ thị liên thông
c. Đường đi ngắn nhất
d. Cây khung trọng lượng tối tiểu
e. Luồng cực đại
2. SỐ HỌC
a. Lý thuyết chia hết
b. Lý thuyết đồng dư
3
CƠ SỞ LOGIC (1)
A. PHÉP TÍNH MỆNH ĐỀ & VỊ TỪ
–Mệnh đề
–Chân trị của mệnh đề: đúng, sai (true, false)
–Các phép toán mệnh đề
•Phép phủ định (NOT, ¬, …)
•Phép hội (AND, ∧)
•Phép tuyển: (OR, ∨)
•Phép tuyển loại trừ (XOR, ⊕)
•Phép toán trên bit
•Phép kéo theo: →
•Phép tương đương: ↔
–Biểu thức mệnh đề
–Mệnh đề hệ quả & mệnh đề tương đương
•Hằng đúng (tautology), hằng sai
•Tiếp liên
•Mệnh đề hệ quả: P → Q hằng đúng
•Tương đương logic: P ↔ Q hằng đúng
4
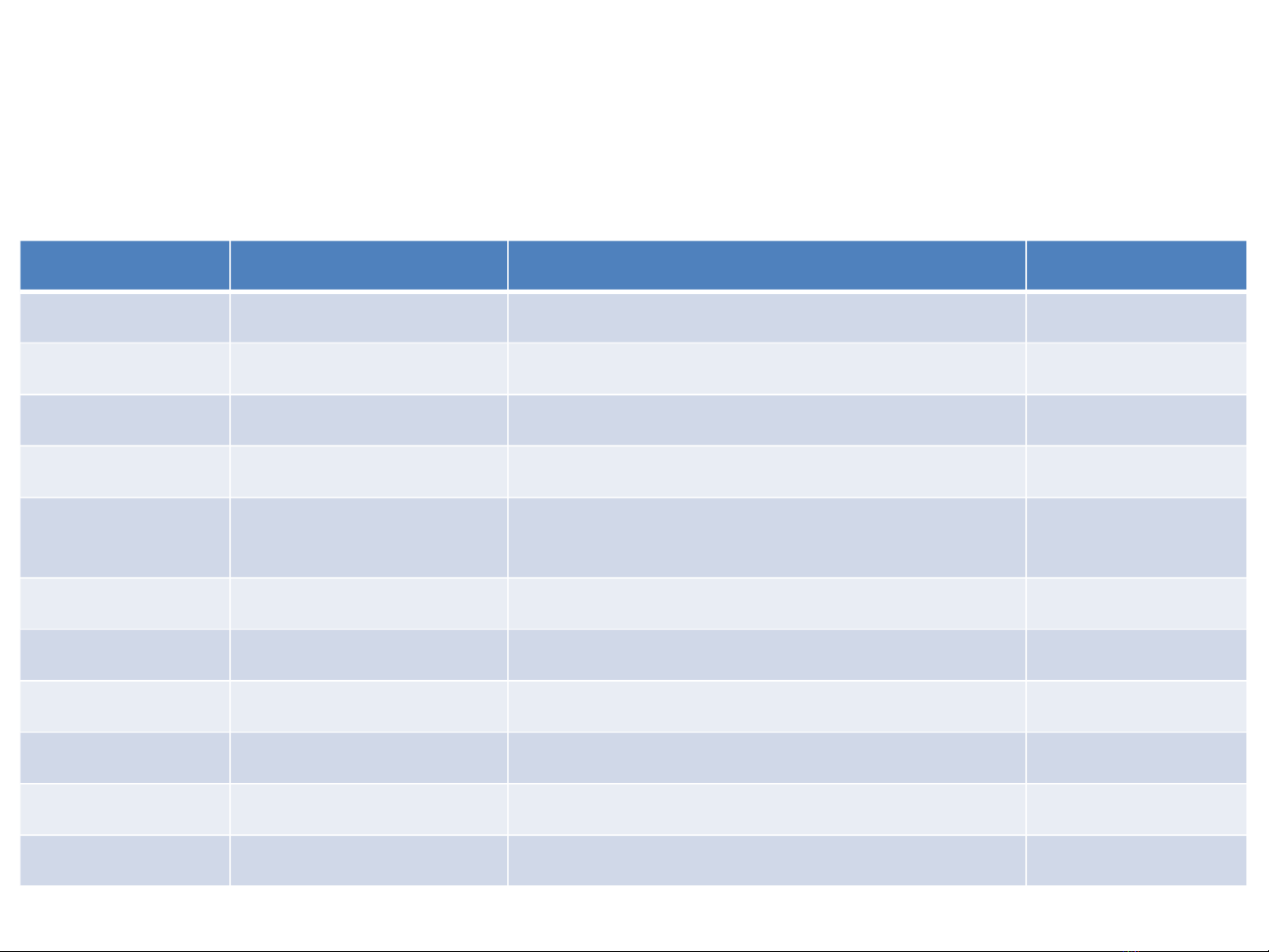
CƠ SỞ LOGIC (2)
Các tương đương thường dùng (T=hằng đúng, F=hằng sai)
P ∨ T = T Domination laws (P ∨ Q) ∨ R=P ∨ (Q ∨ R) = P ∨ Q ∨ R Associative laws
P ∧ F = F (P ∧ Q) ∧ R = P ∧ (Q ∧ R) = P ∧ Q ∧ R
P ∨ F = P Identity laws P ∨ (Q ∧ R)=(P∨Q) ∧ (P∧R) Distributive laws
P ∧ T = P P ∧ (Q ∨R)=(P∧Q) ∨ (P∧R)
P ∨ P = P Idempotent laws ¬(P ∨ Q) = ¬P ∧ ¬Q De Morgan’s
laws
P ∧ P = P ¬(P ∧ Q) = ¬P ∨ ¬Q
¬(¬P)=P Double negation laws P ∨ (P ∧ Q) = P Absortion laws
P ∨ ¬P = T Comlement laws P ∧ (P ∨ Q) = P
P ∧ ¬P = F P → Q = ¬P ∨ Q
P ∨ Q = Q ∨ P Commutative laws
P ∧ Q = Q ∧ P
5