TÓM TẮT KIẾN THỨC TOÁN LỚP 10
PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
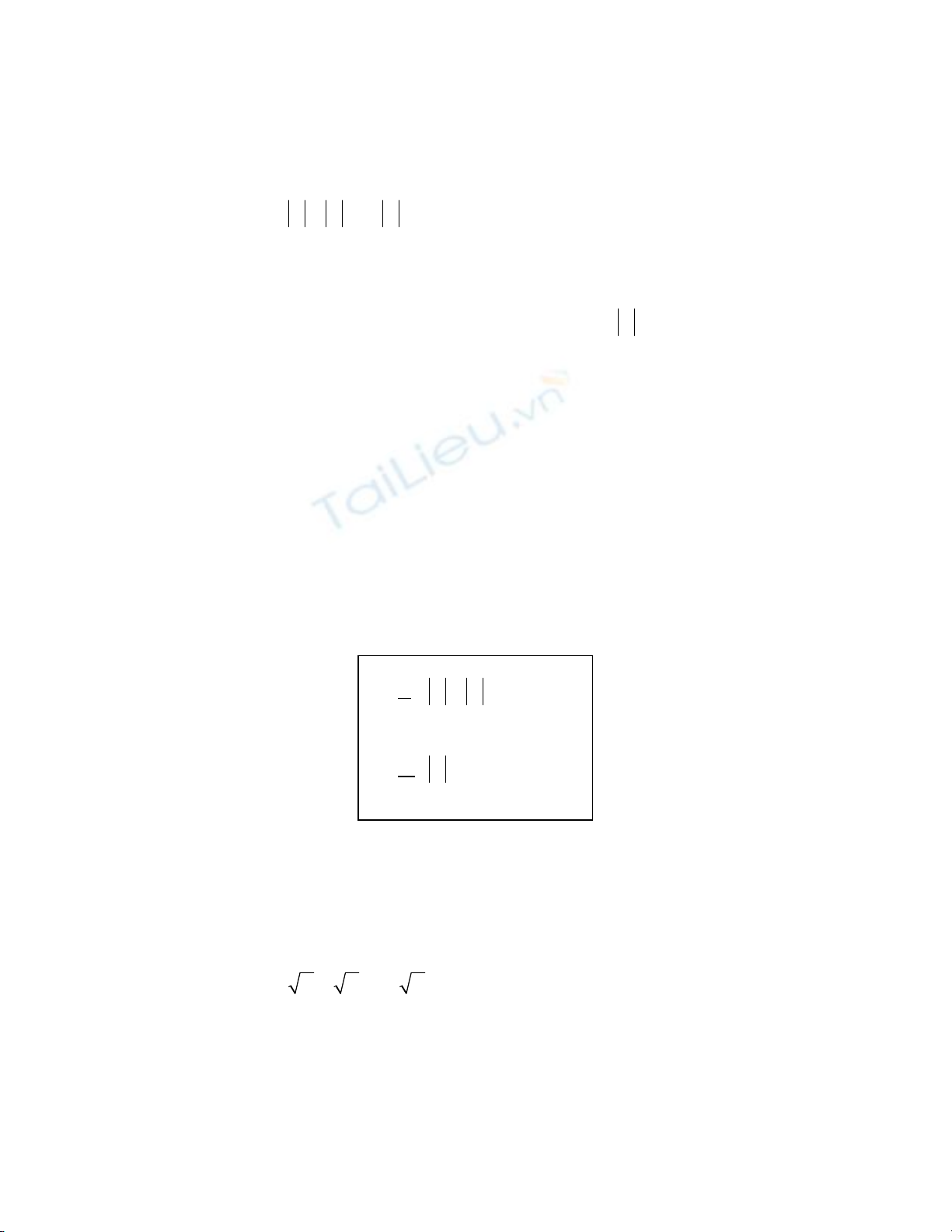
I. Phương trình chứa ẩn trong dấu giá trị tuyệt đối:
Các dạng cơ bản: i)
A B
, ii)
A B
Cách giải 1: Dùng định nghĩa trị tuyệt đối để bỏ trị tuyệt đối:
0
0
A neáu A
AA neáu A
Cách giải 2: Bình phương hai vế dẫn đến phương trình hệ quả. Khi giải xong phải thử lại
nghiệm để loại nghiệm ngoại lai.
Cách giải 3: Dùng công thức:
II. Phương trình chứa ẩn dưới dấu căn:
Các dạng cơ bản: i)
, ii)
A B
A B
A B
A B
0
B
A B
A B
A B
Cách giải 1: Bình phương hai vế dẫn đến phương trình hệ quả. Khi giải xong phải thử lại
nghiệm để loại nghiệm ngoại lai.
Cách giải 2: Dùng công thức:
III. Phương trình và hệ phương trình bậc nhất nhiều ẩn:
1. Phương trình bậc nhất hai ẩn: ax + by + c = 0 (2). Trong đó a, b, c là các hệ số, a và
b không đồng thời bằng 0.
Cặp (x0;y0) được gọi là nghiệm của phương trình (2) nếu chúng nghiệm đúng
phương trình (2).
2. Hệ hai phương trình bậc nhất hai ẩn:
1 1 1
2 2 2
a x b y c
a x b y c
.
Cách giải: Có 3 cách:
0 ( 0)
A hoaëcB
A B A B
2
0
B
A B
A B
1. Dùng phương pháp cộng đại số.
2. Dùng phương pháp thế.
3. Dùng định thức:
Đặt
1 1
2 2
a b
D
a b
,
1 1
2 2
x
c b
D
c b
,
1 1
2 2
y
a c
D
a c
* Nếu
0
x y
D D D
thì hệ có vô số nghiệm
* Nếu
0, 0 0
x y
D D hoaëcD
thì hệ vô nghiệm.
* Nếu
0
D
thì hệ có 1 nghiệm
x
y
D
x
D
D
y
D
3. Hệ ba phương trình bậc nhất ba ẩn:
1 1 1 1
2 2 2 2
3 3 3 3
a x b y c z d
a x b y c z d
a x b y c z d
Cách giải:Khử dần từng ẩn số để đưa hệ phương trình trình về dạng tam giác:
1 1
2 2 2
3 3 3 3
a x d
a x b y d
a x b y c z d
(pp Gausse)
4. Hệ phương trình gồm một bậc nhất và một bậc hai đối với 2 ẩn:
Ví dụ: 2 2
3 4
2 4
x x y y
x y
Cách giải:
- Từ phương trình bậc nhất ta rút một ẩn theo ẩn kia rồi thế vào phương trình bậc
hai ta được phương trình bậc hai một ẩn.
- Giải phương trình bậc hai ta tìm được nghiệm, thay nghiệm vừa tìm vào phương
trình bậc nhất ta tìm được nghiệm của ẩn còn lại.
5. Hệ phương trình đối xứng loại 1: