
1
B GIÁO DC VÀ ĐÀO TO
ĐI HC ĐÀ NNG
HUỲNH NGC TUN
M RNG MÔ HÌNH HI QUY
TUYN TÍNH HAI BIN
Chuyên ngành : PHƯƠNG PHÁP TOÁN SƠ CP
Mã s: 60.46.40
TÓM TT LUN VĂN THC SĨ KHOA HC
Đà Nng - Năm 2012
2
Công trình ñưc hoàn thành ti
ĐI HC ĐÀ NNG
Ngưi hưng dn khoa hc: TS. CAO VĂN NUÔI
Phn bin 1: TS. NGUYN DUY THÁI SƠN
Phn bin 2: GS.TS. LÊ VĂN THUYT
Lun văn ñưc bo v ti Hi ñng chm lun văn tt nghip
Thc sĩ khoa hc hp ti Đi hc Đà Nng vào ngày 02
tháng 02 năm 2012.
* Có th tìm hiu lun văn ti:
- Trung tâm Thông tin - Hc liu, Đi hc Đà Nng
- Thư vin trưng Đi hc Sư phm, Đi hc Đà Nng

3
M ĐU
1. LÝ DO CHN Đ TÀI
Vic xác ñnh mt cách ñnh lưng trong kinh t ñưc kho sát khá
k trong b môn kinh t lưng. B môn này, ra ñi vào nhng năm
1930 ca th k XX, cho ñn nay môn khoa hc này ñã ñem li cho
các nhà kinh t mt công c sc bén, nht là trong ưc lưng, kim
ñnh các quan h kinh t, d báo các thay ñ i kinh t vĩ mô quan
trng như lãi sut, t! l lm phát, GDP…các mô hình kinh t như:
Hi quy tuyn tính, mô hình log tuyn tính, mô hình n"a log
(semilog),....
Hin nay giáo trình và tài liu trình bày mt cách có h thng kin
th#c v$ m% rng mô hình hi quy tuyn tính t ng quát trong kinh t
lưng b&ng ngôn ng toán hc vn còn hn ch. Vì vy, tôi chn ñ$
tài “M RNG MÔ HÌNH HI QUY TUYN TÍNH HAI
BIN” ñ làm lun văn tt nghip ca mình.
2. MC ĐÍCH NGHIÊN CU
Tác gi rt hi vng ñây s' là tài liu tham kho b ích v$ m% rng
mô hình hi quy tuyn tính hai bin và áp dng ca nó trong thc t.
3. Đ I TƯ!NG VÀ PHM VI NGHIÊN CU
3.1. Đi tư%ng: Áp dng mô hình hi quy trong kinh t lưng.
3.2. Ph&m vi nghiên c'u: Mô hình hi quy tuyn tính hai bin và
m% rng mô hình hi quy tuyn tính hai bin.
4. PHƯƠNG PHÁP NGHIÊN CU
Tham kho, phân tích, t ng hp, h thng các tài liu chuyên kho
và các bài báo trên internet khác nhau có liên quan ñn hi quy tuyn
tính và #ng dng trong mt s vn ñ$ kinh t. T( ñó trình bày mt
4
cách có h thng vi các ví d minh ha ñ)y ñ cho ph)n lý thuyt
ñã trình bày.
5. Ý NGHĨA KHOA HC VÀ TH+C TIN C,A Đ TÀI
5.1. Ý nghĩa khoa h1c: H thng kin th#c v$ “m% rng mô hình hi
quy tuyn tính hai bin” và #ng dng vào gii mt s bài toán kinh t
lưng da trên s liu thc t.
5.2. Ý nghĩa th2c ti3n: Đ$ tài hoàn thành tr% thành tài liu tham
kho cho giáo viên, sinh viên % các trưng ñi hc và cao ñ4ng, các
bn yêu toán và các #ng dng ca toán trong kinh t, ñ6c bit là kinh
t lưng.
6. CU TRÚC LUN VĂN
Lun văn gm 3 chương:
CHƯƠNG 1. MÔ HÌNH HI QUY TUYN TÍNH C4 ĐI5N
Đnh nghĩa mô hình hi quy tuyn tính cơ bn và các tích cht liên
quan.
CHƯƠNG 2. CÁC M RNG C,A HI QUY TUYN TÍNH
HAI BIN
Trình bày s m% rng v$ hi quy tuyn tính hai bin.
CHƯƠNG 3. MT S ÁP DNG C,A CÁC MÔ HÌNH M
RNG T6 MÔ HÌNH HI QUY TUYN TÍNH HAI BIN
Trình bày mt s áp dng ca mô hình hi quy tuyn tính hai bin
m% rng.
5
CHƯƠNG 1. MÔ HÌNH HI QUY TUYN TÍNH
C4 ĐI5N
1.1. KHÁI NI7M HÀM HI QUY ĐÁM ĐÔNG
Gi thit r&ng mt cm dân cư có 60 h dân. Gi s" r&ng chúng ta
ch! quan tâm ñn vic nghiên c#u mi quan h gia ñi lưng Y tiêu
dùng hàng tu)n và ñi lưng X kh năng thu nhp kh dng ca m8i
gia ñình.
Gi s" chúng ta chia 60 gia ñình này thành 10 nhóm có thu nhp xp
x! nhau và ñánh giá thu chi ca các gia ñình này trong t(ng nhóm thu
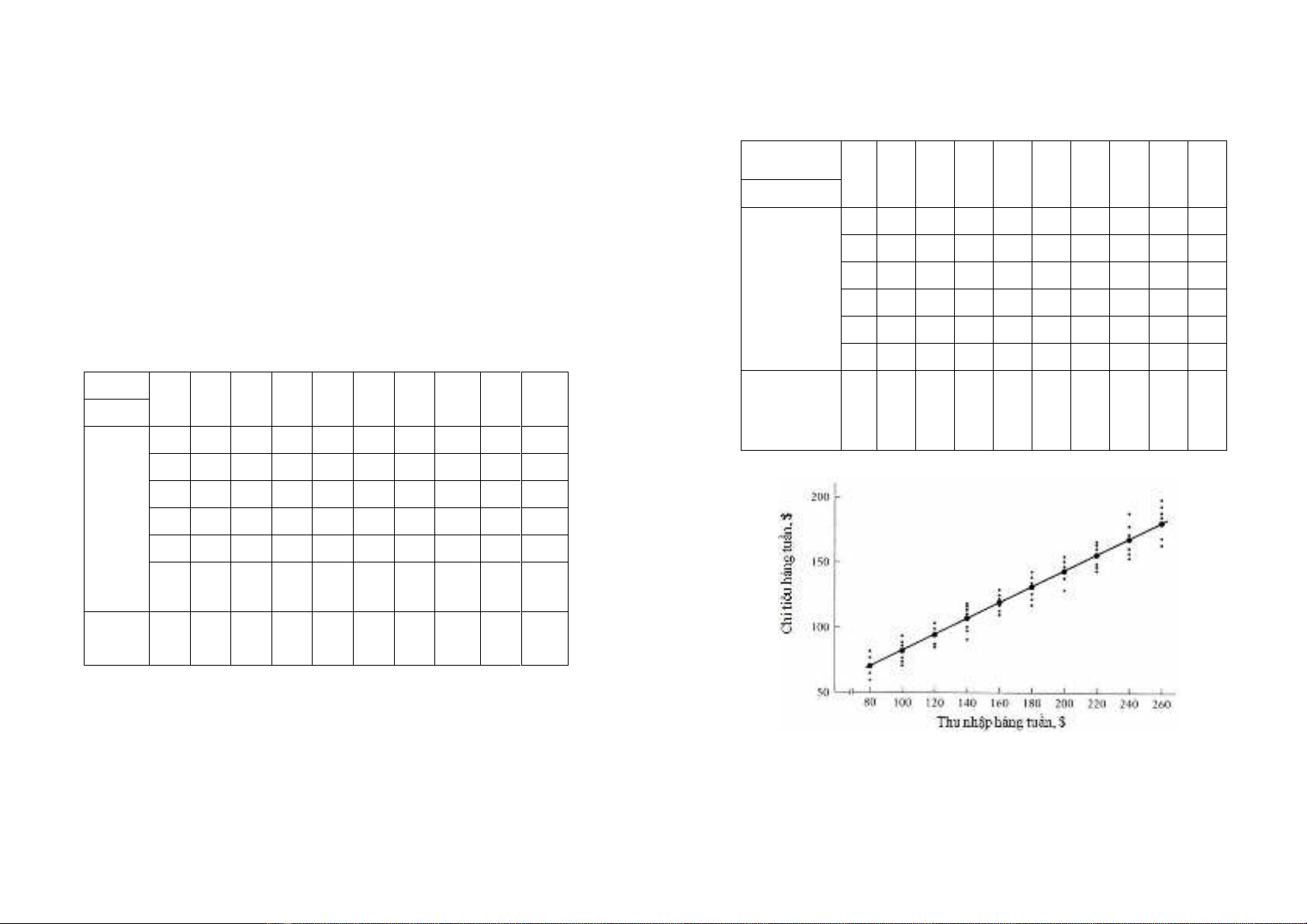
nhp. S liu ñưc cho b%i bng sau:
B8ng 1.1. S liu thu nhp ca 60 gia ñình
X
→
Y
↓
80 100 120 140 160 180 200 220 240 260
55 65 79 102 102 110 120 135 137 150
60 70 84 93 107 115 136 137 145 152
65 74 90 95 110 120 140 140 155 175
70 80 94 103 116 135 145 157 175 180
- 88 -- 113 125 140 - 160 189 185
Chi tiêu
tiêu
dùng
gia ñình
hàng
tu)n Y,
$ - - - 115 - - - 162 - 191
T ng
cng 325 462 445 707 678 750 685 1043 966 1211
Bng 1.1, các giá tr trung bình ca Y tăng khi X tăng. Nu chúng
ta tp trung vào các ñim có kích thưc ln ñ th hin các giá tr
trung bình ca Y thì các trung bình có ñi$u kin này n&m trên mt
ñưng th4ng vi mt ñ dc dương. Đưng th4ng này ñưc gi là
ñưng hi quy t ng th.
6
T( bng trên ta tính ñưc:
B8ng 1.2. Các thông s v$ xác sut và trung bình
X
→
(
)
|
i
p Y X
↓
80 100 120 140 160 180 200 220 240 260
1/5 1/6 1/5 1/7 1/6 1/6 1/5 1/7 1/6 1/7
1/5 1/6 1/5 1/7 1/6 1/6 1/5 1/7 1/6 1/7
1/5 1/6 1/5 1/7 1/6 1/6 1/5 1/7 1/6 1/7
1/5 1/6 1/5 1/7 1/6 1/6 1/5 1/7 1/6 1/7
- 1/6 - 1/7 1/6 1/6 - 1/7 1/6 1/7
Xác sut có
ñi$u kin
(
)
|
i
p Y X
- - - 1/7 - - - 1/7 - 1/7
Trung bình
có ñi$u kin
ca Y
65 77 89 101 113 125 137 149 161 173
Bng 1.2 ñưc th hin qua các hình sau:
Hình 1.1. Phân phi có ñi$u kin ca chi tiêu ñi vi
m#c ñ thu nhp khác nhau ca Bng 1.1
7
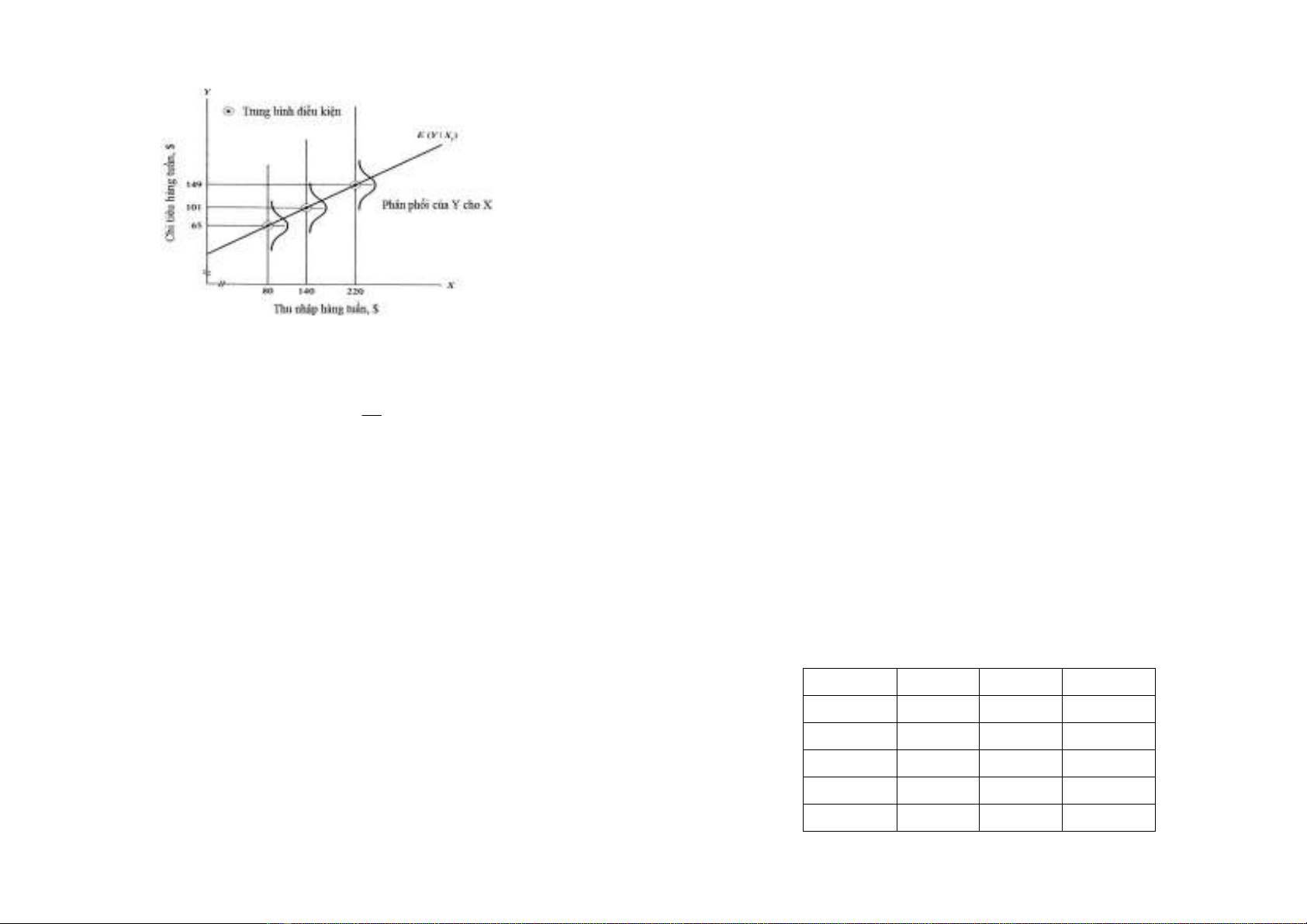
Hình 1.2. Đưng hi quy t ng th ca Bng 1.2
T( hình 1.1 và 1.2, ta nhn thy r&ng m8i trung bình có ñi$u kin
E(Y|X
i
) là mt hàm ca
i
X
. Kí hiu:
(
)
(
)
| , 1,
i i
E Y X f X i n
= = (1.1)
trong ñó,
(
)
i
f X
là hàm ca bin gii thích
i
X
, phương trình (1.1)
ñưc gi là hàm hi quy t ng th hai bin (Population Regression
Function - PRF) hay ngn gn hơn là hi quy t ng th (Population
Regression - PR). Theo Keynes, hàm tiêu dùng Y theo thu nhp X
như sau:
(
)
1 2
|
i i
E Y X X
β β
= + (1.2)
trong ñó,
1 2
,
β β
gi là h s hi quy.
Phương trình (1.2) ñưc gi là hàm hi quy t ng th tuyn tính.
1.2. Ý NGHĨA C,A THUT NG9 “TUYN TÍNH”
1.2.1. S2 tuy:n tính theo các bi:n s
Đó là kỳ vng có ñi$u kin ca Y là mt hàm tuyn tính ca
i
X
.
V$ m6t hình hc, ñưng cong tuyn tính trong trưng hp này là
ñưng th4ng.
8
1.2.2. S2 tuy:n tính theo các tham s
Đó là kỳ vng có ñi$u kin ca Y,
(
)
|
i
E Y X
là mt hàm tuyn
tính theo các tham s
β
ca nó. Theo các hiu này thì nó có th
tuyn tính ho6c không tuyn tính theo bin X.
1.3. SAI S NG;U NHIÊN
T( hình 1.1, nhn thy r&ng vi mt m#c thu nhp
i
X
, m#c chi
tiêu ca mt h gia ñình có th n&m xung quanh giá tr trung bình ca
các h gia ñình có thu nhp
i
X
. Đi$u này ta có th di:n t ñ lch ca
i
Y
xung quanh giá tr kỳ vng ca nó:
(
)
|
i i i
Y E T X u
= +
(1.3)
trong ñó, ñ lch
i
u
là bin s ngu nhiên không th quan sát.
V$ thut ng chuyên môn, ta gi
i
u
là s hng nhi:u ngu nhiên hay
s hng sai s ngu nhiên. Công th#c (1.3) có th cho chúng ta bit
r&ng chi tiêu ca mt gia ñình khi bit m#c thu nhp ca h:
(1)
(
)
|
i
E T X
chi tiêu trung bình ca tt c các gia ñình có cùng thu
nhp (yu t này tt yu).
(2)
i
u
yu t ngu nhiên hay không h thng.
1.4. HÀM HI QUY M;U
Chúng ta c)n phi tính PRF trên cơ s% thông tin mu. Gi thit
r&ng ta không có thông tin gì v$ Bng 1.1 và ta ch! có thông tin ngu
nhiên tương #ng các giá tr Y vi X (ñưc cho % bng sau).
B8ng 1.3. Mu ngu nhiên t( t ng th bng 1.1 (1)
Y X Y X
70 80 115 180
65 100 120 200
90 120 140 220
95 140 155 140
110 160 150 260

9
T( Bng 1.3 ta có th d ñoán ñưc chi tiêu trung bình hàng tu)n Y
trong t ng th tương #ng X ñưc chn không? Hay ta có th tính
ñưc PRF t( bng d liu mu hay không? Vic tính này cũng ñ6t ra
nghi vn không tính chính xác ñưc PRF b%i vì có s dao ñng trong
vic ly mu. Gi s" ta ly ngu nhiên mt mu ngu nhiên khác t(
bng 1.1.
B8ng 1.4. Mu ngu nhiên t( t ng th bng 1.1 (2)
Y X Y X
55 80 120 180
88 100 145 200
90 120 125 220
80 140 145 240
118 160 175 260
T( bng 1.3 và 1.4, chúng ta ñưc ñ th phân tán như sau:
Hình 1.3. Đưng hi quy mu ca 2 mu bng 1.3 và 1.4
Biu th#c tương #ng vi (1.2) có th ñưc vit li:
1 2
ˆ ˆ
ˆ
i i
Y X
β β
= + (1.8)
10
Tóm li, mc tiêu chính ca ta trong phân tích hi quy là tính PRF
1 2
i i i
Y X u
β β
= + +
(1.4)
Trên cơ s% ca SRF
1 2
ˆ ˆ
ˆ
ˆ
i i i
Y X u
β β
= + +
(1.9)
1.5. MÔ HÌNH HI QUY TUYN TÍNH C4 ĐI5N
1.5.1. Ư<c lư%ng các h= s c>a mô hình h?i quy b@ng phương
pháp bình phương ti thiBu thông thưCng OLS (Ordinary Least
Square)
1.5.1.1. Các gi ñnh ca mô hình hi quy tuyn tính c ñin
1.5.1.2. Phương pháp bình phương ti thiu thông thưng
T( hàm hi quy (1.9):
1 2
ˆ ˆ
i i i
u Y X
β β
= − −
vy
( )
2
21 2
1 1
ˆ ˆ
n n
i i i
i i
u Y X
β β
= =
= − −
∑ ∑ (1.10)
Đi$u kin ñ (1.10) ñt cc tr là:
X
ˆ
Y
ˆ
21
β−=β (1.15)
1
2
2
1
ˆ
n
i i
i
n
i
i
y x
x
β
=
=
=
∑
∑
(1.17)
vi XXx
ii
−= và YYy
ii
−= .
1.5.1.3. Tính cht ca hàm hi quy mu theo OLS
Tính chDt c>a ư<c lư%ng tham s:
(1)
1
ˆ
β và
2
ˆ
β là duy nht #ng vi mt mu xác ñnh gm n quan sát
(Xi,Yi).
(2)
1
ˆ
β và
2
ˆ
β là các ưc lưng ñim ca β
1
và β
2
. Giá tr ca
1
ˆ
β và
2
ˆ
β thay ñ i theo mu dùng ñ ưc lưng.


























