TÓM T T LÝ THUY T VÀ CÔNG TH C GI I BÀI T P CH NG DAO ĐNG CẮ Ế Ứ Ả Ậ ƯƠ Ộ Ơ
A. LÝ THUY TẾ
1. DAO ĐNG ĐI U HOÀỘ Ề
* Dao đng c , dao đng tu n hoànộ ơ ộ ầ
+ Dao đng c là chuy n đng qua l i c a v t quanh 1 v trí cân b ng.ộ ơ ể ộ ạ ủ ậ ị ằ
+ Dao đng tu n hoàn là dao đng mà sau nh ng kho ng th i gian b ng nhau v t tr l i v trí và chi uộ ầ ộ ữ ả ờ ằ ậ ở ạ ị ề
chuy n đng nh cũ (tr l i tr ng thái ban đu).ể ộ ư ở ạ ạ ầ
* Dao đng đi u hòaộ ề
+ Dao đng đi u hòa là dao đng trong đó li đ c a v t là m t hàm côsin (ho c sin) c a th i gian.ộ ề ộ ộ ủ ậ ộ ặ ủ ờ
+ Ph ng trình dao đng: x = Acos(ươ ộ t + )
Trong đó: x (m;cm ho c rad): Li đ (to đ) c a v t; cho bi t đ l ch và chi u l ch c a v t so v iặ ộ ạ ộ ủ ậ ế ộ ệ ề ệ ủ ậ ớ
VTCB.
A>0 (m;cm ho c rad): Là biên đ (li đ c c đi c a v t); cho bi t đ l ch c c đi c a v t soặ ộ ộ ự ạ ủ ậ ế ộ ệ ự ạ ủ ậ
v i VTCB.ớ
(t + ) (rad): Là pha c a dao đng t i th i đi m t; cho bi t tr ng thái dao đng (v trí vàủ ộ ạ ờ ể ế ạ ộ ị
chi u chuy n đng) c a ề ể ộ ủ
v t th i đi m t.ậ ở ờ ể
(rad): Là pha ban đu c a dao đng; cho bi t tr ng thái ban đu c a v t.ầ ủ ộ ế ạ ầ ủ ậ
(rad/s): Là t n s góc c a dao đng đi u hoà; cho bi t t c đ bi n thiên góc phaầ ố ủ ộ ề ế ố ộ ế
+ Đi m P dao đng đi u hòa trên m t đo n th ng luôn luôn có th d c coi là hình chi u c a m tể ộ ề ộ ạ ẳ ể ượ ế ủ ộ
đi m M chuy n đng tròn đu trên đng kính là đo n th ng đó.ể ể ộ ề ườ ạ ẳ
* Chu k , t n s c a dao đng đi u hoàỳ ầ ố ủ ộ ề
+ Chu kì T(s): Là kho ng th i gian đ th c hi n m t dao đng toàn ph n.ả ờ ể ự ệ ộ ộ ầ
Chính là kho ng th i gian ng n nh t đ v t tr l i v trí và chi u chuy n đng nh cũ (tr l i tr ngả ờ ắ ấ ể ậ ở ạ ị ề ể ộ ư ở ạ ạ
thái ban đu).ầ
+ T n s f(Hz):Là s dao đng toàn ph n th c hi n đc trong m t giây.ầ ố ố ộ ầ ự ệ ượ ộ
+ Liên h gi a ệ ữ , T và f: =
T
2
= 2f.
* V n t c và gia t c c a v t dao đng đi u hoàậ ố ố ủ ậ ộ ề
+ V n t c là đo hàm b c nh t c a li đ theo th i gian: v = x' = - ậ ố ạ ậ ấ ủ ộ ờ Asin(t + ) = Acos(t + +
2
)
V n t c c a v t dao đng đi u hòa bi n thiên đi u hòa cùng t n s nh ng s m pha h n ậ ố ủ ậ ộ ề ế ề ầ ố ư ớ ơ
2
so v iớ
v i li đ. ớ ộ
- v trí biên (x = Ở ị A): Đ l n ộ ớ vmin = 0
- v trí cân b ng (x = 0): Đ l n Ở ị ằ ộ ớ vmin =A.
Giá tr đi s : vị ạ ố max = A khi v>0 (v t chuy n đng theo chi u d ng qua v trí cân b ng)ậ ể ộ ề ươ ị ằ
vmin = -A khi v<0 (v t chuy n đng theo chi u âm qua v trí cân b ng)ậ ể ộ ề ị ằ
+ Gia t c là đo hàm b c nh t c a v n t c (đo hàm b c 2 c a li đ) theo th i gian: a = v' = x’’ = -ố ạ ậ ấ ủ ậ ố ạ ậ ủ ộ ờ
2Acos(t + ) = - 2x
Gia t c c a v t dao đng đi u hòa bi n thiên đi u hòa cùng t n s nh ng ng c pha v i li đ (s mố ủ ậ ộ ề ế ề ầ ố ư ượ ớ ộ ớ
pha
2
so v i v n t c).ớ ậ ố
Véc t gia t c c a v t dao đng đi u hòa luôn h ng v v trí cân b ng và t l v i đ l n c a li đ.ơ ố ủ ậ ộ ề ướ ề ị ằ ỉ ệ ớ ộ ớ ủ ộ
- v trí biên (x = Ở ị A), gia t c có đ l n c c điố ộ ớ ự ạ : amax = 2A.
Giá tr đi s : aị ạ ố max=2A khi x=-A; amin=-2A khi x=A;.
- v trí cân b ng (x = 0), gia t c b ng 0.Ở ị ằ ố ằ

+ Đ th c a dao đng đi u hòa là m t đng hình sin.ồ ị ủ ộ ề ộ ườ
+ Qu đo dao đng đi u hoà là m t đo n th ng.ỹ ạ ộ ề ộ ạ ẳ
* Dao đng t do (dao đng riêng)ộ ự ộ
+ Là dao đng c a h x y ra d i tác d ng ch c a n i l cộ ủ ệ ả ướ ụ ỉ ủ ộ ự
+ Là dao đng có t n s (t n s góc, chu k ) ch ph thu c các đc tính c a h không ph thu c cácộ ầ ố ầ ố ỳ ỉ ụ ộ ặ ủ ệ ụ ộ
y u t bên ngoài.ế ố
Khi đó: g i là t n s góc riêng; f g i là t n s riêng; T g i là chu k riêngọ ầ ố ọ ầ ố ọ ỳ
2. CON L C LÒ XO.Ắ
* Con l c lò xoắ
+ Con l c lò xo g m m t lò xo có đ c ng k, kh i l ng không đáng k , m t đu g n c đnh, đu kiaắ ồ ộ ộ ứ ố ượ ể ộ ầ ắ ố ị ầ
g n v i v t n ng kh i l ng m đc đt theo ph ng ngang ho c treo th ng đng.ắ ớ ậ ặ ố ượ ượ ặ ươ ặ ẳ ứ
+ Con l c lò xo là m t h dao đng đi u hòa. ắ ộ ệ ộ ề
+ Ph ng trình dao đng: x = Acos(ươ ộ t + ).
+ V i: ớ =
m
k
+ Chu kì dao đng c a con l c lò xo: T = 2ộ ủ ắ
k
m
.
+ L c gây ra dao đng đi u hòa luôn luôn h ng v v trí cân b ng và đc g i là l c kéo v hay l cự ộ ề ướ ề ị ằ ượ ọ ự ề ự
h i ph c. L c kéo v có đ l n t l v i li đ và là l c gây ra gia t c cho v t dao đng đi u hòa.ồ ụ ự ề ộ ớ ỉ ệ ớ ộ ự ố ậ ộ ề
Bi u th c đi s c a l c kéo v : F = - kx.ể ứ ạ ố ủ ự ề
L c kéo v c a con l c lò xo không ph thu c vào kh i l ng v t. ự ề ủ ắ ụ ộ ố ượ ậ
* Năng l ng c a con l c lò xoượ ủ ắ
+ Đng năngộ : Wđ =
2
1
mv2 =
2
1
m2A2sin2(t+).
+ Th năng: Wết =
2
1
kx2 =
2
1
k A2cos2(t + )
Đng năng và th năng c a v t dao đng đi u hòa bi n thiên v i t n s góc ộ ế ủ ậ ộ ề ế ớ ầ ố ’=2, t n s f’=2f vàầ ố
chu kì T’=
2
T
.
+ C năng: W = Wơt + Wđ =
2
1
k A2 =
2
1
m2A2 = h ng s .ằ ố
C năng c a con l c t l v i bình ph ng biên đ dao đng. ơ ủ ắ ỉ ệ ớ ươ ộ ộ
C năng c a con l c lò xo không ph thu c vào kh i l ng v t.ơ ủ ắ ụ ộ ố ượ ậ
C năng c a con l c đc b o toàn n u b qua m i ma sát.ơ ủ ắ ượ ả ế ỏ ọ
3. CON L C ĐNẮ Ơ
* Con l c đnắ ơ
+ Con l c đn g m m t v t n ng treo vào s i dây không gi n, v t n ng kích th c không đáng k soắ ơ ồ ộ ậ ặ ợ ả ậ ặ ướ ể
v i chi u dài s i dây, s i dây kh i l ng không đáng k so v i kh i l ng c a v t n ng.ớ ề ợ ợ ố ượ ể ớ ố ượ ủ ậ ặ
+ Khi dao đng nh (sinộ ỏ (rad)), con l c đn dao đng đi u hòa v i ph ng trình: ắ ơ ộ ề ớ ươ
s = Socos(t + ) ho c ặ = o cos(t + ); v i ớ =
l
s
; o =
l
So
+ Chu k , t n s , t n s góc: T = 2ỳ ầ ố ầ ố
g
l
; f =
2
1
l
g
; =
l
g
.
+ L c kéo v khi biên đ góc nh : F = - ự ề ộ ỏ
s
l
mg
=-mg
+ Xác đnh gia t c r i t do nh con l c đnị ố ơ ự ờ ắ ơ : g =
2
2
4
T
l
.

+ Chu kì dao đng c a con l c đn ph thu c đ cao, đ sâu, vĩ đ đa lí và nhi t đ môi tr ng. ộ ủ ắ ơ ụ ộ ộ ộ ộ ị ệ ộ ườ
* Năng l ng c a con l c đnượ ủ ắ ơ
+ Đng năngộ : Wđ =
2
1
mv2
+ Th năng: Wết = mgl(1 - cos) =
2
1
mgl2 ( 1rad, (rad)).
+ C năng: W = Wơt + Wđ = mgl(1 - cos0) =
2
1
mgl
2
0
.
C năng c a con l c đn đc b o toàn n u b qua ma sát.ơ ủ ắ ơ ượ ả ế ỏ
4. DAO ĐNG T T D N, DAO ĐNG C NG B CỘ Ắ Ầ Ộ ƯỞ Ứ
* Dao đng t t d nộ ắ ầ
+ Là dao đng có biên đ gi m d n theo th i gian (năng l ng gi m d n theo th i gian).ộ ộ ả ầ ờ ượ ả ầ ờ
+ Nguyên nhân: Do môi tr ng có đ nh t (có ma sát, l c c n) làm tiêu hao năng l ng c a h .ườ ộ ớ ự ả ượ ủ ệ
+ Khi l c c n c a môi tr ng nh có th coi dao đng t t d n là đi u hoà (trong kho ng vài ba chuự ả ủ ườ ỏ ể ộ ắ ầ ề ả
k )ỳ
+ Khi coi môi tr ng t o nên l c c n thu c v h dao đng (l c c n là n i l c) thì dao đng t t d nườ ạ ự ả ộ ề ệ ộ ự ả ộ ự ộ ắ ầ
có th coi là dao đng t do.ể ộ ự
+ ng d ng: Các thi t b đóng c a t đng hay gi m xóc ô tô, xe máy, … là nh ng ng d ng c a daoỨ ụ ế ị ử ự ộ ả ữ ứ ụ ủ
đng t t d n.ộ ắ ầ
* Dao đng duy trìộ
+ Là dao đng (t t d n) đc duy trì mà không làm thay đi chu k riêng c a h .ộ ắ ầ ượ ổ ỳ ủ ệ
+ Cách duy trì: Cung c p thêm năng l ng cho h b ng l ng năng l ng tiêu hao sau m i chu k .ấ ượ ệ ằ ượ ượ ỗ ỳ
+ Đc đi m: - Có tính đi u hoàặ ể ề
- Có t n s b ng t n s riêng c a h .ầ ố ằ ầ ố ủ ệ
* Dao đng c ng b cộ ưỡ ứ
+ Là dao đng x y ra d i tác d ng c a ngo i l c bi n thiên tu n hoàn.ộ ả ướ ụ ủ ạ ự ế ầ
+ Đc đi m: - Có tính đi u hoàặ ể ề
- Có t n s b ng t n s c a ngo i l c (l c c ng b c)ầ ố ằ ầ ố ủ ạ ự ự ưỡ ứ
- Có biên đ ph thu c biên đ c a ngo i l c, t n s l c c ng b c và l c c n c a môiộ ụ ộ ộ ủ ạ ự ầ ố ự ưỡ ứ ự ả ủ
tr ng.ườ
Biên đ dao đng c ng b c t l v i biên đ ngo i l c.ộ ộ ưỡ ứ ỷ ệ ớ ộ ạ ự
Đ chênh l ch gi a t n s l c c ng b c và t n s riêng càng nh thì biên đ dao đngộ ệ ữ ầ ố ự ưỡ ứ ầ ố ỏ ộ ộ
c ng b c càng l n.ưỡ ứ ớ
L c c n c a môi tr ng càng nh thì biên đ dao đng c ng b c càng l n.ự ả ủ ườ ỏ ộ ộ ưỡ ứ ớ
* C ng h ngộ ưở
+ Là hi n t ng biên đ c a doa đng c ng b c đt giá tr c c đi khi t n s l c c ng b c b ngệ ượ ộ ủ ộ ưỡ ứ ạ ị ự ạ ầ ố ự ưỡ ứ ằ
t n s riêng c a h .ầ ố ủ ệ
+ Đng cong bi u di n s ph thu c c a biên đ vào t n s c ng b c g i là đ th c ng h ng.ườ ể ễ ự ụ ộ ủ ộ ầ ố ưở ứ ọ ồ ị ộ ưở
Nó càng nh n khi l c c n c a môi tr ng càng nh .ọ ự ả ủ ườ ỏ
+ Hi n t ng c ng h ng x y ra càng rõ nét khi l c c n (đ nh t c a môi tr ng) càng nh .ệ ượ ộ ưở ả ự ả ộ ớ ủ ườ ỏ
+ T m quan tr ng c a hi n t ng c ng h ng:ầ ọ ủ ệ ượ ộ ưở
Nh ng h dao đng nh tòa nhà, c u, b máy, khung xe, ... đu có t n s riêng. Ph i c n th n khôngữ ệ ộ ư ầ ệ ề ầ ố ả ẩ ậ
đ cho các h y ch u tác d ng c a các l c c ng b c m nh, có t n s b ng t n s riêng đ tránh sể ệ ấ ị ụ ủ ự ưở ứ ạ ầ ố ằ ầ ố ể ự
c ng h ng, gây dao đng m nh làm gãy, đ.ộ ưở ộ ạ ổ
H p đàn c a đàn ghi ta, viôlon, ... là nh ng h p c ng h ng v i nhi u t n s khác nhau c a dây đànộ ủ ữ ộ ộ ưở ớ ề ầ ố ủ
làm cho ti ng đàn nghe to, rõ.ế
5. T NG H P DAO ĐNG ĐI U HOÀỔ Ợ Ộ Ề
+ Dao đng t ng h p c a hai (ho c nhi u) dao đng đi u hoà cùng ph ng cùngộ ổ ợ ủ ặ ề ộ ề ươ
t n s là m t dao đng đi u hoà cùng ph ng cùng t n s .ầ ố ộ ộ ề ươ ầ ố

+ N u m t v t tham gia đng th i hai dao đng đi u hoà cùng ph ng, cùng t n s v i các ph ngế ộ ậ ồ ờ ộ ề ươ ầ ố ớ ươ
trình: x1 = A1cos(t + 1) và x2 = A2cos(t + 2)
Thì dao đng t ng h p s là: x = xộ ổ ợ ẽ 1 + x2 = Acos(t + )
V i: Aớ2 =A12+A22+2A1A2cos(2-1)
tan =
2211
2211
coscos
sinsin
AA
AA
Biên đ và pha ban đu c a dao đng t ng h p ph thu c vào biên đ và pha ban đu c a các daoộ ầ ủ ộ ổ ợ ụ ộ ộ ầ ủ
đng thành ph n.ộ ầ
+ Khi hai dao đng thành ph n cùng pha (ộ ầ 2 - 1 = 2k) thì dao đng t ng h p có biên đ c c đi: A =ộ ổ ợ ộ ự ạ
A1 + A2
+ Khi hai dao đng thành ph n ng c pha (ộ ầ ượ 2 - 1) = (2k + 1)) thì dao đng t ng h p có biên đ c cộ ổ ợ ộ ự
ti u: A = |Aể1 - A2| .
+ Khi hai dao đng thành ph n vuông pha ộ ầ
2 1
(2 1) 2
k
π
ϕ ϕ
− = +
thì dao đng t ng h p có biên đ:ộ ổ ợ ộ
2 2
1 2
A A A= +
+ Tr ng h p t ng quát: |Aườ ợ ổ 1 - A2| ≤ A ≤ A1 + A2
B. CÁC CÔNG TH CỨ
I. DAO ĐNG ĐI U HOÀỘ Ề
1. Ph ng trình dao đng: x = Acos(ươ ộ t + )
2. V n t c t c th i: v = -ậ ố ứ ờ Asin(t + ) = Acos(t + +
2
π
)
V n t c trung bình c a v t t th i đi m tậ ố ủ ậ ừ ờ ể 1 (có li đ xộ1) đn th i đi m tế ờ ể 2 (có li đ xộ2):
2 1
2 1
x x
vt t
−
=−
v
r
luôn cùng chi u v i chi u chuy n đng (v t chuy n đng theo chi u d ng thì v>0, theo chi uề ớ ề ể ộ ậ ể ộ ề ươ ề
âm thì v<0)
3. Gia t c t c th i: a = -ố ứ ờ 2Acos(t + ) = 2Acos(t + +)
a
r
luôn h ng v v trí cân b ngướ ề ị ằ
4. V t VTCB: x = 0; ậ ở vMax = A; aMin = 0
V t biên: x = ±A; ậ ở vMin = 0; aMax = 2A
Nh v y ư ậ đ l nộ ớ vMin = 0 và aMax = 2A khi v t biên còn ậ ở vMax = A và aMin = 0 khi v t VTCB.ậ ở
Giá tr đi sị ạ ố vmax=A khi v t qua v trí cân b ng theo chi u d ng.ậ ị ằ ề ươ
vmin=-A khi v t qua v trí cân b ng theo chi u âm.ậ ị ằ ề
amax=2A khi v t biên x=-A.ậ ở
amin=-2A khi v t biên x=A.ậ ở
5. H th c đc l p: ệ ứ ộ ậ
2 2 2
( )
v
A x
ω
= +
2 2
2
4 2
a v A
ω ω
+ =
a = -2x
6. C năng: ơ
2 2
đ
1
W W W 2
t
m A
ω
= + =
V i ớ
2 2 2 2 2
đ
1 1
W sin ( ) Wsin ( )
2 2
mv m A t t
ω ω ϕ ω ϕ
= = + = +
2 2 2 2 2 2
1 1
W ( ) W s ( )
2 2
t
m x m A cos t co t
ω ω ω ϕ ω ϕ
= = + = +
- Tìm v trí c a v t khi đng năng b ng n l n th năng đàn h i:ị ủ ậ ộ ằ ầ ế ồ
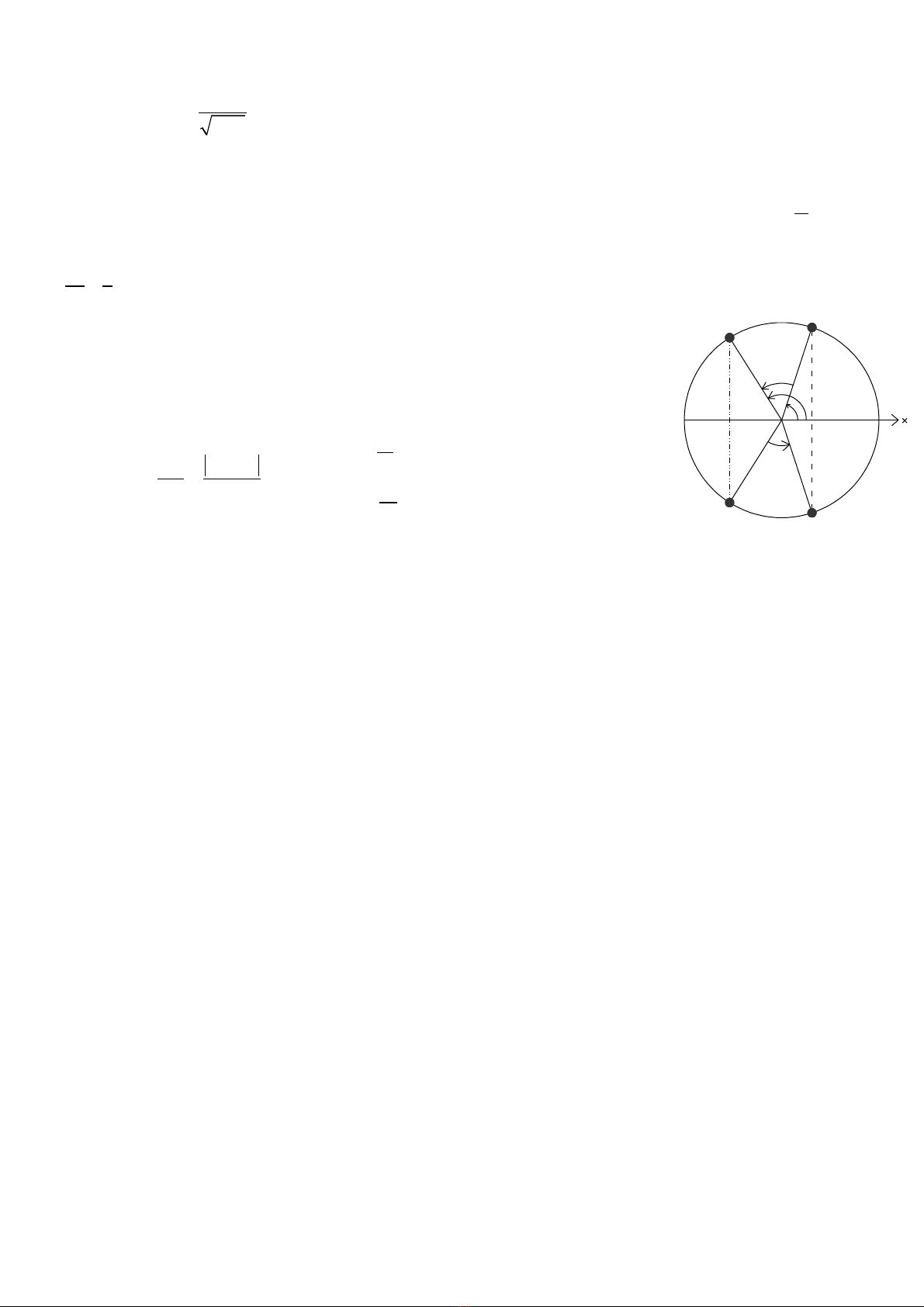
1
d t
A
w nw x n
= = +
7. Dao đng đi u hoà có t n s góc là ộ ề ầ ố , t n s f, chu k T. Thì đng năng và th năng bi n thiên v iầ ố ỳ ộ ế ế ớ
t n s góc 2ầ ố , t n s 2f, chu k T/2ầ ố ỳ
- Trong m t chu k có 4 l n wộ ỳ ầ đ = wt ,kho ng th i gian gi a hai l n liên ti p đ wả ờ ữ ầ ế ể đ = wt là
4
T
t∆ =
8. Đng năng và th năng trung bình trong th i gian nT/2 ( nộ ế ờ N*, T là chu k dao đng) là:ỳ ộ
2 2
W 1
2 4 m A
ω
=
9. Chi u dài qu đo: 2Aề ỹ ạ
10. Quãng đng đi trong 1 chu k luôn là 4A; trong 1/2 chu k luôn là 2Aườ ỳ ỳ
Quãng đng đi trong l/4 chu k là A khi v t đi t VTCB đn v trí biênườ ỳ ậ ừ ế ị
ho c ng c l iặ ượ ạ
11. Kho ng th i gian ng n nh t đ v t đi t v trí có li đ xả ờ ắ ấ ể ậ ừ ị ộ 1 đn xế2
2 1
t
ϕ ϕ
ϕ
ω ω
−
∆
∆ = =
v i ớ
1
1
2
2
s
s
x
co A
x
co A
ϕ
ϕ
=
=
và (
1 2
0 ,
ϕ ϕ π
)
12. Các b c gi i bài toán tính th i đi m v t đi qua v trí đã bi t x (ho c v,ướ ả ờ ể ậ ị ế ặ
a, Wt, Wđ, F) l n th nầ ứ
* Ph ng pháp l ng giác:ươ ượ
+ Gi i ph ng trình l ng giác l y các nghi m c a t (V i t > 0 ả ươ ượ ấ ệ ủ ớ ph m vi giá tr c a k )ạ ị ủ
+ Li t kê n nghi m đu tiên (th ng n nh )ệ ệ ầ ườ ỏ
+ Th i đi m th n chính là giá tr l n th n c a t.ờ ể ứ ị ớ ứ ủ
* Ph ng pháp đng tròn:ươ ườ
+ T ph ng trình dao đng xác đnh v trí xu t phát c a v t t ng ng trên đng tròn Mừ ươ ộ ị ị ấ ủ ậ ươ ứ ườ 0.
+ Xác đnh v trí c n tính th i đi m v t đi qua trên đng tròn Mị ị ầ ờ ể ậ ườ 1, M2…
+ Xác đnh góc quét c a bán kính (véc t quay) khi v t qua v trí x l n th n.ị ủ ơ ậ ị ầ ứ
L u ý:ư + Véc t quay theo chi u d ng l ng giác. V t chuy n đng theo chi u d ng Ox ng v iơ ề ươ ượ ậ ể ộ ề ươ ứ ớ
đi m n m n a d i đng tròn còn chuy n đng theo chi u âm n m n a trên đng tròn.ể ằ ử ườ ườ ể ộ ề ằ ở ử ườ
+ M i v trí c a v t có li đ x s ng v i 2 đi m n m trên đng tròn (đi m n m n a trênỗ ị ủ ậ ộ ẽ ứ ớ ể ằ ườ ể ằ ử
chuy n đng theo chi u âm, đi m n m n a d i chuy n đng theo chi u d ng). Tr v trí biên chể ộ ề ể ằ ử ướ ể ộ ề ươ ừ ị ỉ
có m t đi m.ộ ể
+ M i chu k (m i dao đng) ng v i m t vòng (góc quét 2ỗ ỳ ỗ ộ ứ ớ ộ ) v t qua m i đi m trên đngậ ỗ ể ườ
tròn 1 l n.ầ
13. Các b c gi i bài toán tìm s l n v t đi qua v trí đã bi t x (ho c v, a, Wướ ả ố ầ ậ ị ế ặ t, Wđ, F) t th i đi m từ ờ ể 1
đn tế2.
* Ph ng pháp l ng giác:ươ ượ
+ Gi i ph ng trình l ng giác đc các nghi m c a t.ả ươ ượ ượ ệ ủ
+ T từ1 < t ≤ t2 Ph m vi giá tr c a (V i k ạ ị ủ ớ Z)
+ T ng s giá tr c a k chính là s l n v t đi qua v trí đó.ổ ố ị ủ ố ầ ậ ị
* Ph ng pháp đng tròn:ươ ườ
+ Xác đnh v trí xu t phát Mị ị ấ 0và v trí đích M t ng ng c a v t trên đng tròn b ng cách tính gócị ươ ứ ủ ậ ườ ằ
pha
1=t1+ và 2=t2+.
+ Xác đnh các v trí v t đi qua Mị ị ậ 1, M2… t ng ng trên đng tròn.ươ ứ ườ
A
-A x1x2
M2 M1
M'1
M'2
O


























