Ch ng IVươ
TRUY N NHI T VÀ THI T B TRAO Ề Ệ Ế Ị
Đ I NHI TỔ Ệ
IV.1. M T S KHÁI NI MỘ Ố Ệ
IV.2. CÁC BÀI TOÁN TRUY N NHI TỀ Ệ
IV.3. THI T B TRAO Đ I NHI TẾ Ị Ổ Ệ
IV.1.1. Khái ni m truy n nhi tệ ề ệ
- Trao đ i nhi t gi a các v t có nhi t đ ổ ệ ữ ậ ệ ộ
khác nhau.
- G m nhi u ph ng th c trao đ i nhi t ồ ề ươ ứ ổ ệ
x y ra đ ng th i.ả ồ ờ
IV.1. M T S KHÁI NI MỘ Ố Ệ
IV.1.2. Ph ng pháp gi i bài toán ươ ả
truy n nhi tề ệ
• Ph ng pháp 1 ươ
Phân tích quá trình truy n nhi t và ch n ra ề ệ ọ
ph ng th c trao đ i nhi t đóng vai trò ươ ứ ổ ệ
quy t đ nh r i áp d ng công th c cho ế ị ồ ụ ứ
ph ng th c trao đ i nhi t đó. Các ươ ứ ổ ệ
ph ng th c khác đ c tính đ n b ng ươ ứ ượ ế ằ
cách đ a vào các h s hi u ch nh.ư ệ ố ệ ỉ
Ph ng pháp 2ươ
Áp d ng công th c:ụ ứ Q = k.∆t.F
Q = k.(tf1 – tf2).F ; [W]
Trong đó:
Q [W]- công su t nhi t c a thi t bấ ệ ủ ế ị
F [m2]- di n tích b m t trao đ i ệ ề ặ ổ
nhi tệ
k[W/m2K]- h s truy n nhi t ệ ố ề ệ
∆t=(tf1-tf2)
IV.2. CÁC BÀI TOÁN TRUY N NHI T Ề Ệ
C B N Ơ Ả
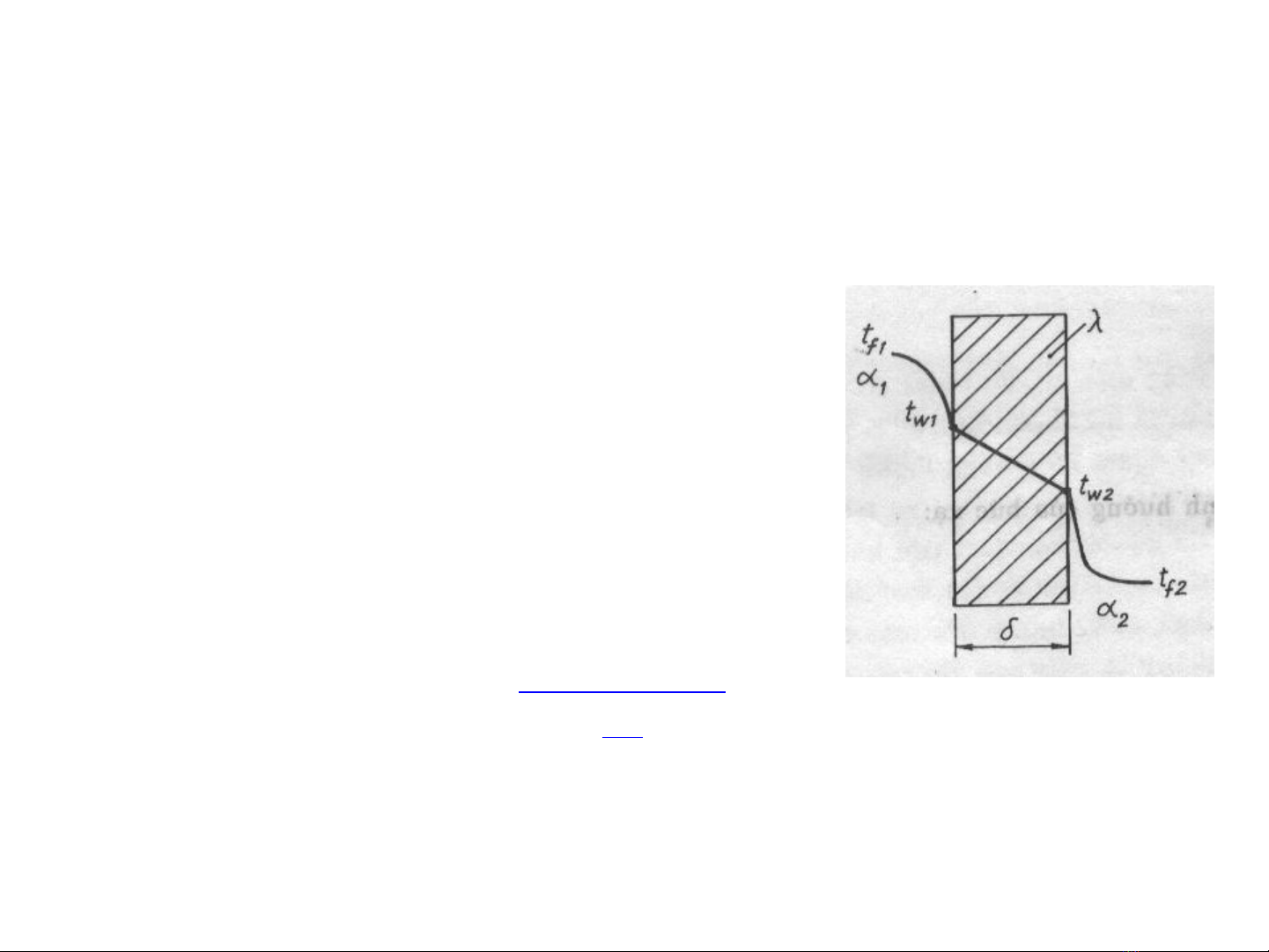
IV.2.1. Truy n nhi t qua vách ph ngề ệ ẳ
• Gi thi t:ả ế
• K t lu n:ế ậ
( )
1 1 f1 w1
q t t
= α −
w1 w 2
2
t t
q
−
=δ
λ
( )
3 2 w2 f 2
q t t
= α −