TRUY N THÔNG SỀ Ố
DIGITAL COMMUNICATION
Week 9
Reference
•“Digital communications: Fundamentals and Applications” by
Bernard Sklar
•Telecommunication Networks - Information Theory, Vinh
Dang
(*) H Văn Quân – Khoa CNTT – ĐH Bách Khoa TpHCMồ
[1]. R. E. Ziemer & W. H. Transter, “Information Theory and
Coding”, Principles of Communications: Systems,
Modulation, and Noise, 5th edition. John Wiley, pp. 667-720,
2002.
[2]. A. Bruce Carlson, “Communications Systems”, Mc Graw-
Hill, 1986, ISBN 0-07-100560-9
[3]. S. Haykin, “Fundamental Limits in Information Theory”,
Communication Systems, 4th edition, John Wiley & Sons Inc,
Tu n tr cầ ướ
•B gi i mã Maximum likelihoodộ ả
•Quy t đ nh m m / c ng (soft decisions ế ị ề ứ
and hard decisions)
•Gi i thu t Viterbiả ậ
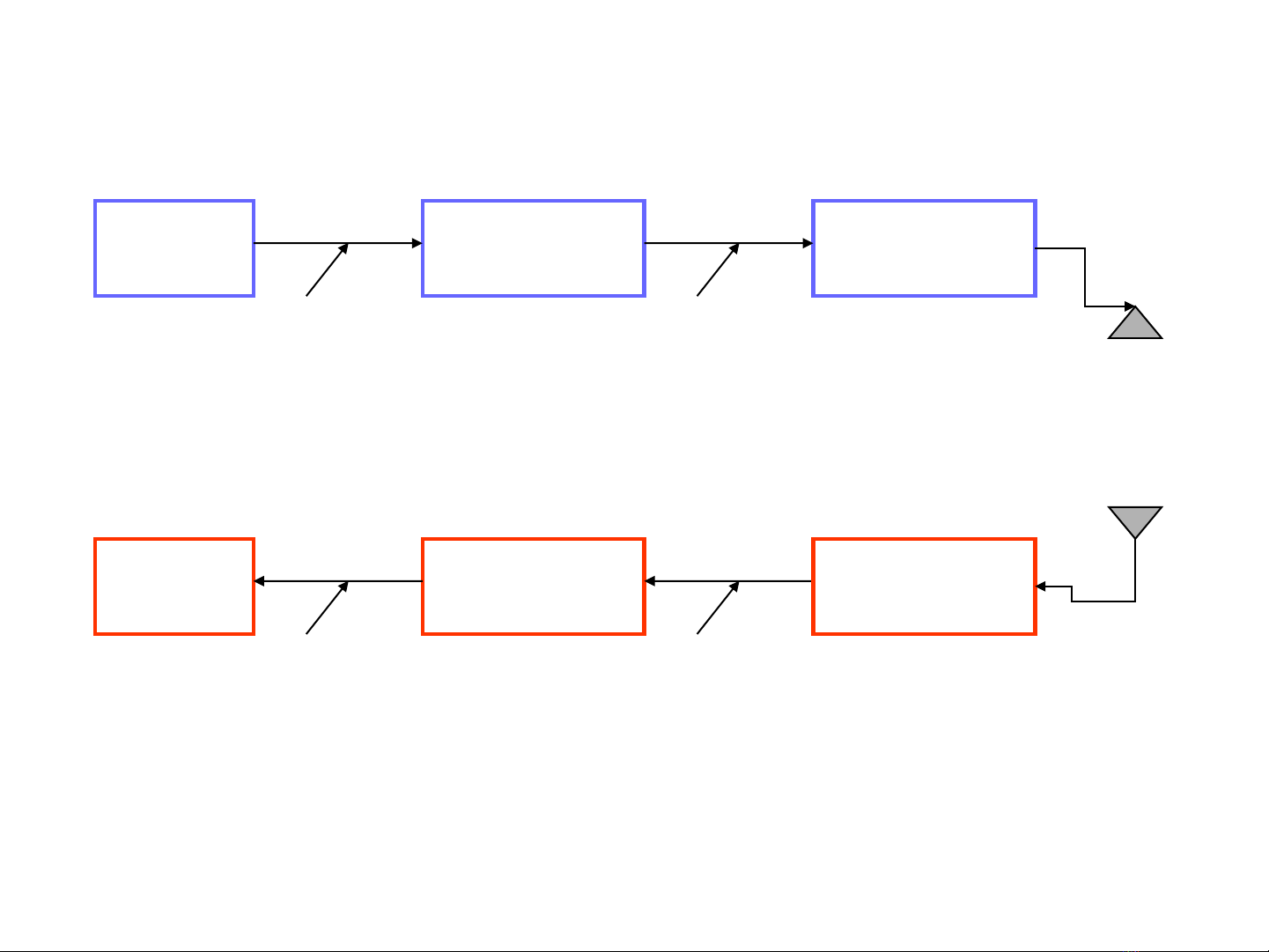
Block diagram of the DCS
dBranch worper outputs
1
dBranch worfor
outputsr Demodulato
sequence received
321
,...),...,,,(
n
nijii
i
i
i
,...,z,...,zzZ
ZZZZ
=
=Z
Information
source
Rate 1/n
Conv. encoder Modulator
Information
sink
Rate 1/n
Conv. decoder Demodulator
sequenceInput
21
,...),...,,(
i
mmm=m
bits) coded ( rdBranch wo
1
sequence Codeword
321
,...),...,,,(
n
nijiii
i
,...,u,...,uuU
UUUU
=
=
=G(m)U
,...)
ˆ
,...,
ˆ
,
ˆ
(
ˆ
21 i
mmm
=
m
Channel
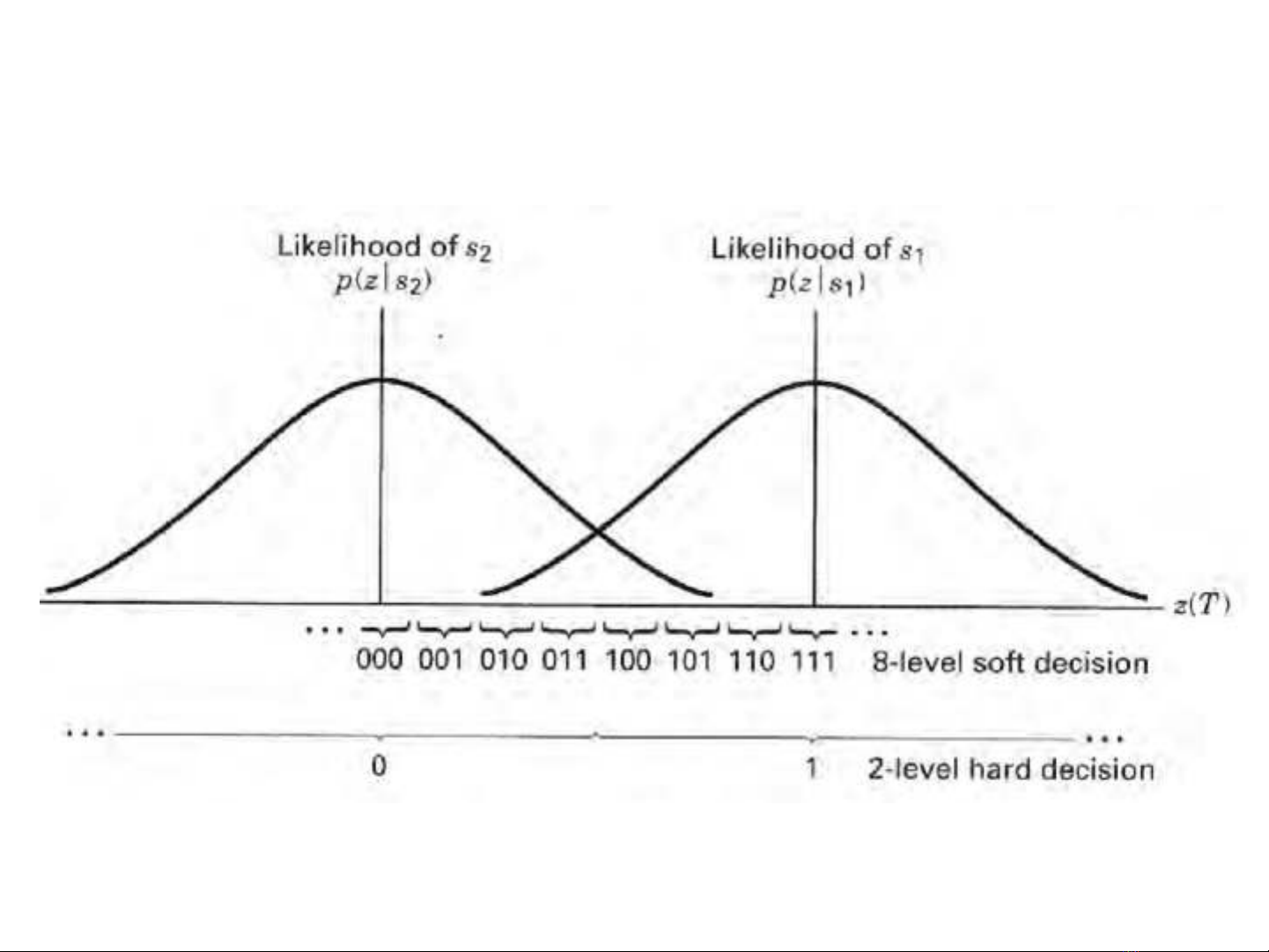
Quy t đ nh m m / c ngế ị ề ứ