224 Antiferromagnetism và tr t t t tínhậ ự ừ
Table 6.4. Critical exponents for the three-dimensional d-vector models
d α β γ δ ν η
0
1
2
Nh aự
Ising
xy
0.236 0.302 1.16 4.85 0.588 0.03
0.110 0.324 1.24 4.82 0.630 0.03
−0.007 0.346 1.32 4.81 0.669 0.03
3Heisenberg −0.115 0.362 1.39 4.82 0.705 0.03
∞ hình c uầ−1 1/2 2 5 1 0
Gi thuy tả ế r ngộ tĩnh cho năng l ngượ mi n phíễ và ch c năngứ
t ng quanươ
ng ýụ r ngằ ch cóỉ hai trong s cácố s mũố th c sự ự đ c l pộ ậ . Họ có
liên quan
b iở các đ ngẳ như
2 = α + 2β + γ ,
γ = β (δ − 1),
α = 2 − νD,
(2 − η)ν = γ .
Các tr ngườ s mũố có nghĩa là, là α = 0, β =12 , γ= 1, δ = 3, ν
=12andη = 0.
Lý thuy tế tr ngườ trung bình c aủ m tộ ho cặ antiferromagnet s tắ
từ m tộ tài kho nả không
đúng cho nh ng bi n đ ngữ ế ộ quan tr ngọ th c sự ự đ cượ quan sát
th yấ khi D = 3, nh ngư
khi D = 4, theo các đ ngẳ, lý thuy tế có thể là chính xác! Các
dimen-
sion n iơ lĩnh v cự lý thuy tế có nghĩa là chính xác đ c g iượ ọ là
chi u kíchề quan tr ngọ trên.
Nói chung trong khu v cự quan tr ngọ, g n ầTC, các ph ng trìnhươ
tr ng tháiạ có th đ c vi tể ượ ế
(5.14)
(H /M)γ = a(T − TC) −
bM1/β.
(6.29)
Các s mũố quan tr ngọ đã đ cượ tính toán s l ngố ượ khi có
không có gi i phápả phân tích, s d ngử ụ ph ng phápươ tái chu nẩ
hóa nhóm phát tri nể b iở
Kenneth Wilson, Leo Kadanoff và nh ng ng i khácữ ườ . Các thu cộ
tính c aủ b n g cả ố
m ng tinh thạ ể đ cượ so sánh v iớ nh ng ng iữ ườ trong m ngạ m tộ
m r ngở ộ c aủ m tộ nhân r ngộ fac-
tor. Nó ch raỉ r ngằ t lỉ ệ l p đi l p l iặ ặ ạ b oả v t lýậ c aủ các quan
tr ngọ
khu v cự. Giá tr c aị ủ th c tự ế quan tr ngọ ba chi uề Heisenberg
mô hình đ c bao g m trongượ ồ B ng 6.4ả. Thành ph nầ quan tr ngọ
cho các mô hình Ising,
bao g mồ các gi i phápả Onsager chính xác trong hai chi uề, đ cượ
thu th pậ t iạ
B ng 6.5ả.
Giá trị c aủ nhi t đệ ộ t i h nớ ạ , các Curie ho cặ đi mể N'eel, không
đ cộ
ch a xongư c u trúcấ m ng tinh thạ ể. Nó cũng có thể đ cượ tính
b ng sằ ố, nó làm tăng
v iớ D và ph i h pố ợ số Z, nh ưtrong B ng 6.6ả, và cũng v iớ
xoay chi uề d. Đ i v iố ớ các mô hình Heisenberg ba chi uề, t lỷ ệ
kBTC / ZJ là 0,61, 0,66 và 0,70 cho các kh iố, bcc và FCC m ngạ
tinh thể đ n gi nơ ả ,
t ng ngươ ứ .
225 6.6 Mô hình từ
B ng 6.5.ảM t vài mô hình Ising s mũ quan tr ng ; D ≥ 4ộ ố ọ
là tr ng h p tr ng trung bình?ườ ợ ườ
D
2
3a
≥4
α
0
1/8
0
β
1/8
5/16
1/2
γ
7/4
5/4
1
δ
15
5
3
ν
1
5/8
1/2
η
1/4
0
0
aGiá tr x p x .ị ấ ỉ
b ng 6.6.ảt su t ỷ ấ kBTC/Z J cho Ising xo n trên dàn ắ
khác nhau
Lattice
Chain
Honeycomb
Square
Triangular
Diamond
Simple cubic
Body-centred cubic
Face-centred cubic
D
1
2
2
2
3
3
3
3
Z
2
3
4
6
4
6
8
12
0
0.506
0.567
0.607
0.676
0.752
0.794
0.916
6.6.3 Xo n - thu tinh lý thuy tắ ỷ ế
Quay v thu tinh xo n, nhi u - th o lu n câu h i v lý thuy tề ỷ ắ ề ả ậ ỏ ề ế
đã đ c ' đó chuy n pha Tf, hay là làm đ ng l c h c xo nượ ở ể ở ộ ự ọ ắ
ti n hoá m t cách liên t c, nh ng theo hàm mũ v i nhi t đ khiế ộ ụ ư ớ ệ ộ
xo n d n đóng băng? Nói cách khác, là làm l nh c a xo n chắ ầ ạ ủ ắ ỉ
c n t ng t v i lo i c a chuy n đ ng phân tán tác d ng t mầ ươ ự ớ ạ ủ ể ộ ụ ầ
xa trong thu tinh thu tinh c a nó chuy n ( khi tên g i c aỷ ở ỷ ủ ể ọ ủ
thu tinh xo n ' s đ ngh ), hay là đó m t vài lo i c a dángỷ ắ ẽ ề ị ở ộ ạ ủ
đi u t p th ng i s n xu t tính kỳ d trong năng l ng c nệ ậ ể ườ ả ấ ị ượ ầ
thi t đ t o ra công có ích hay là đ o hàm c a nó Tf, cũngế ể ạ ạ ủ ở
nh có ư ở
Đi m Curieể
N u có chuy n pha, nó có th đ đ ng nh t hoá tham s th tế ể ể ể ồ ấ ố ứ ự
đóng vai trò t hoá trong ch t s t t hay là t con hoá trongừ ấ ắ ừ ừ
antiferromagnet, và đ 0 Tf. Michigan mômen t đ a ph ng ể ở ừ ị ươ ở
n i ith trung bình trên toàn b n i Michigan không ph i là ch nơ ộ ơ ả ọ
có th , vì nó là s không chút nào nhi t đ . . Nên l y phép chi uể ố ệ ộ ấ ế
c a xo n lên c u hình ng u nhiên riêng, hay là b n sao c a h . .ủ ắ ấ ẫ ả ủ ệ
Có phong c nh năng l ng trong đó c u hình xo n khác nhauả ượ ấ ắ
chi m đóng khác nhau, năng l ng không đ t đ c c c ti u.ế ượ ạ ượ ự ể
Tham s th t là đ nh nghĩa b ng Edwards vàố ứ ự ị ằ
Anderson khi t hoá t phát bình ph ng trung bình trong c cừ ự ươ ự
ti u đ n α, trung bình trên toàn b c c ti u có th :ể ơ ộ ự ể ể
q˜ = Pα m2iα,(6.30)
226
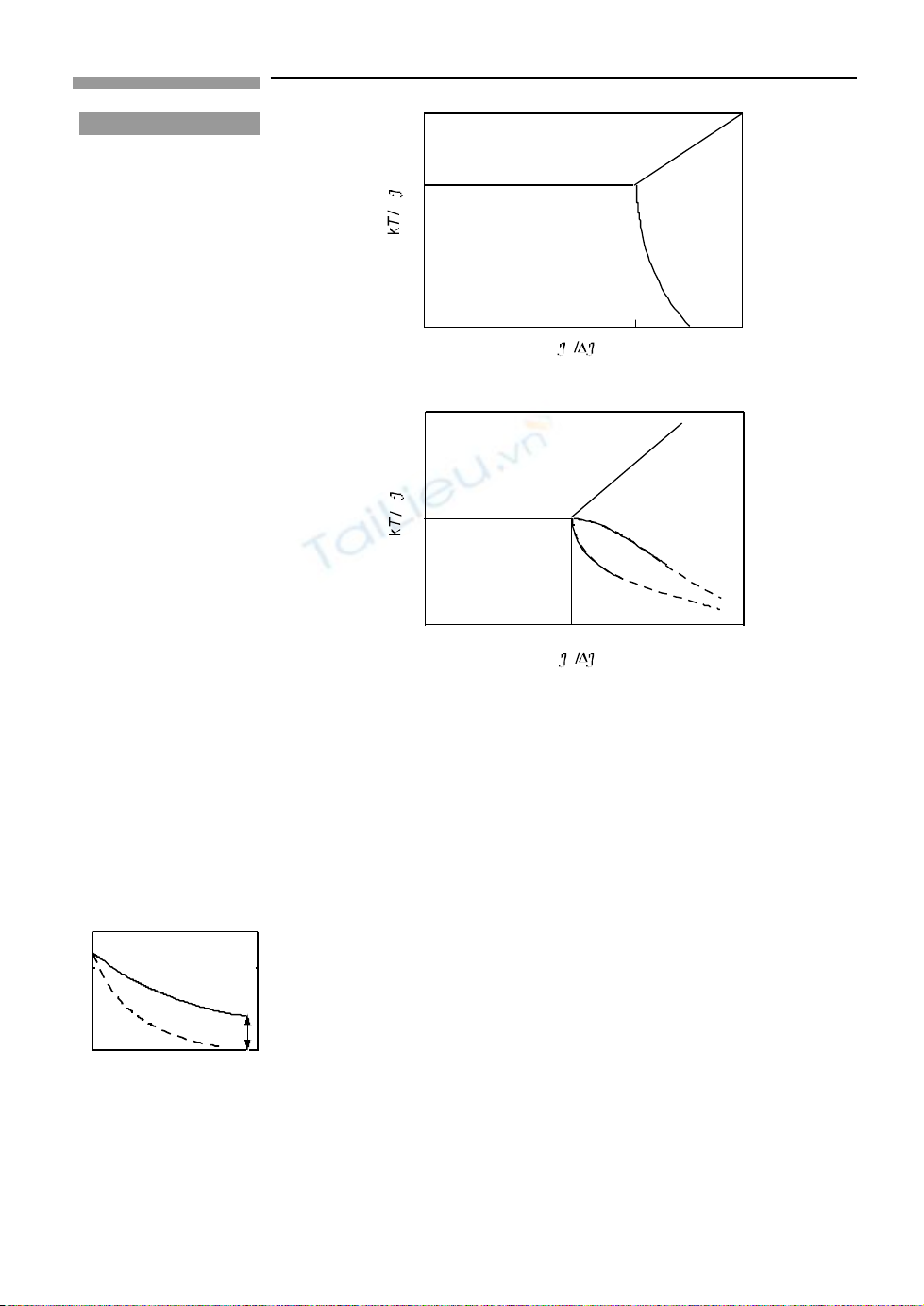
Hình 6.27
S đ pha lý thuy t tính toánơ ồ ế
trong lý thuy t tr ng trung bìnhế ườ
cho ( ) thu tinh xo n Ising b ngỷ ắ ằ
D. Sherrington và
S. Kirkpatrick ( Phys. Rev.
Ch cái 35, 1792 ( 1975 ) ) và ( bữ
) cho xo n vect b ngắ ơ ằ
M. Gabay và G. Toulouse
(Phys. Rev. Letters 47, 201
(1981)). Có phân ph i trao đ iố ổ
qua l i chi u r ng J và J0 giá trạ ề ộ ị
trung bình.
1Th y tinh xo nủ ắ ( T<Tf )
Antiferromagnetism and other magnetic order
Ch t thu n tấ ậ ừ
1
Ch t s t tấ ắ ừ
Th y tinh xo nủ ắ
00 1
0
( a )
Ch t thu n t tấ ậ ừ
Ch t s t tấ ắ ừ
1
M 1
Th y tinh xo nủ ắ
M 2
0 1
0
( b )
trong đó Pα = exp ( - εα/kBT ) / exp ( - εα/kBT ).Liên quan đ nế
tham s th t là tr ng liên h p. Trong phòng thí nghi mố ứ ự ườ ợ ệ
không ph i tr ng nào cũng đ u t i đ c , nh ng m t tr ngả ườ ề ớ ượ ư ộ ườ
chao đ o ng u nhiên khác đ i v i m i c u hình.ả ẫ ố ớ ỗ ấ
Đ c m t ng ng là χ ˜.Fortunaterly, hoá ra χ ˜ đ t đ c, vìộ ả ươ ứ ạ ượ
đ c m phi tuy n χnl, đ nh nghĩa b ngộ ả ế ị ằ
M = χ H − χnlH3,(6.31)
là t l đ χ ˜. ỷ ệ ể
Câu h i c a có hay không có chuy n pha Tfturns ra đ đ cỏ ủ ể ở ể ượ
b t ng tinh t . Ch a bi t ch c h bao gi th c s đ t đ cấ ờ ế ư ế ắ ệ ờ ự ự ạ ượ
cân b ng ~, khi gi m d là lôga đúng lúc.ằ ả ư
ch t thu n t ấ ậ ừ ( T>Tf )~ Nghi m c a mô hìnhệ ủ ,
trong đó có phân b chu n c a t ng tác trao đ i c a J chi uố ẩ ủ ươ ổ ủ ề
r ng, có tâm Jộ ở o,
0t
q đã đ c cho thu tinh xo n Ising trung bình tr ng approxi -ượ ỷ ắ ở ườ
Ph thu c th i gian c a hàm tụ ộ ờ ủ ự
t ng quanươ
N t xi ( 0 ). N t xi ( t ) cho ch tố ố ấ
thu n t và thu tinh xo n.ậ ừ ỷ ắ
mation (Fig. 6.27(a)). Nó ch ng t chuy n lõm vào đ đ u thuứ ỏ ể ể ề ỷ
tinh xo n. Bi u đ cho gi i pháp tr ng trung bình c a mô hìnhắ ể ồ ả ườ ủ
Heisenberg ch ng t chuy n Txy, trong đó thành ph n b ph nứ ỏ ể ầ ộ ậ
c u thành xo n ngang đóng băng, và m t chuy n khác nhi tấ ắ ộ ể ở ệ