7/26/2012
1
CƠ CHT LNG
Th.S BÙI ANH KIT
KHOA XÂY DNG & ðIN
CHƯƠNG 2:
THUTĨNH HC
Tháng 06/2012
Th.S Bùi Anh Kit
NI DUNG
1. Áp sut thutĩnh – Áp lc thutĩnh
2. Tính cht ca áp sut thutĩnh
3. Phương trình vi phân cơbn ca cht lng cân bng
4. Phương trình cơbn ca thutĩnh hc
5. Áp sut tuytñi – áp sut dư– áp sut chân không
6. ðnh lut bình thông nhau
7. ðnh lut Pascan
8. ð phân báp sut thutĩnh – ñ áp lc
9. Áp lc cht lng lên thành phng
10.Áp lc cht lng lên thành cong
7/26/2012
2
Cơslý thuyt
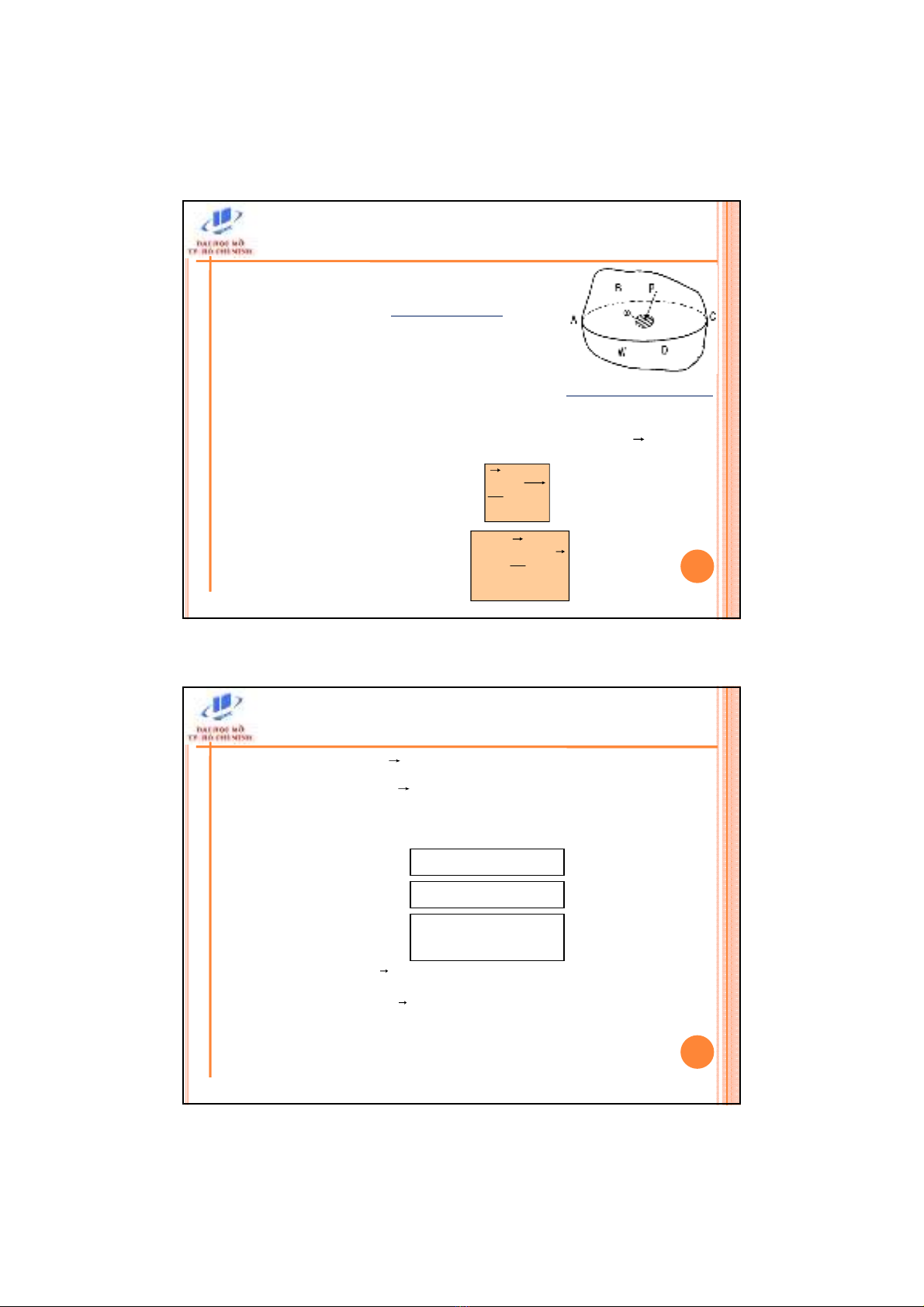
Khi cht lng W ñng cân bng
Ct khi W bng mt phng (ABCD) và
bphn trên
Th.S Bùi Anh Kit
Xét mt din tích ωtrên mt phng (ABCD)
Hlc tương ñương ca phn trên tác dng lên ω:
P
tb
p
ω
P=
p
ω
P
lim
0ω
=
→
Thay thlc tác dng ca phn trên bng hlc tương ñương
Áp sut thutĩnh trung bình:
Áp sut thutĩnh ti 1 ñim:
1. ÁP SUT THUTĨNH –ÁP LC THUTĨNH
Th.S Bùi Anh Kit
Áp sut thutĩnh:
Chú ý: trsp ca cũng ñưc gi là áp sut thutĩnh.
ðơn v: N/m2hoc kg/m.s2; at; m ct nưc.
p
p
P
P
Áp lc thutĩnh:
Chú ý: trsP ca cũng ñưc gi là áp lc thutĩnh.
ðơn v: N
1 at =9,81. 104N/m2
1 at =10m ct H2O
=760mm Hg
1 N/m2= 1Pa
Chuynñiñơn v:
1. ÁP SUT THUTĨNH –ÁP LC THUTĨNH
7/26/2012
3
TÍNH CHT CA ÁP SUT THUTĨNH
Tính cht 1:áp sut thutĩnh tác dng thng góc vi din tích
chu lc và hưng vào din tích y
Th.S Bùi Anh Kit
Tính cht 2:trsáp sut thutĩnh ti mtñim bt kỳkhông
phthuc vào hưng ñt ca din tích chu lc tiñim này
3. PHƯƠNG TRÌNH VI PHÂN CƠBN
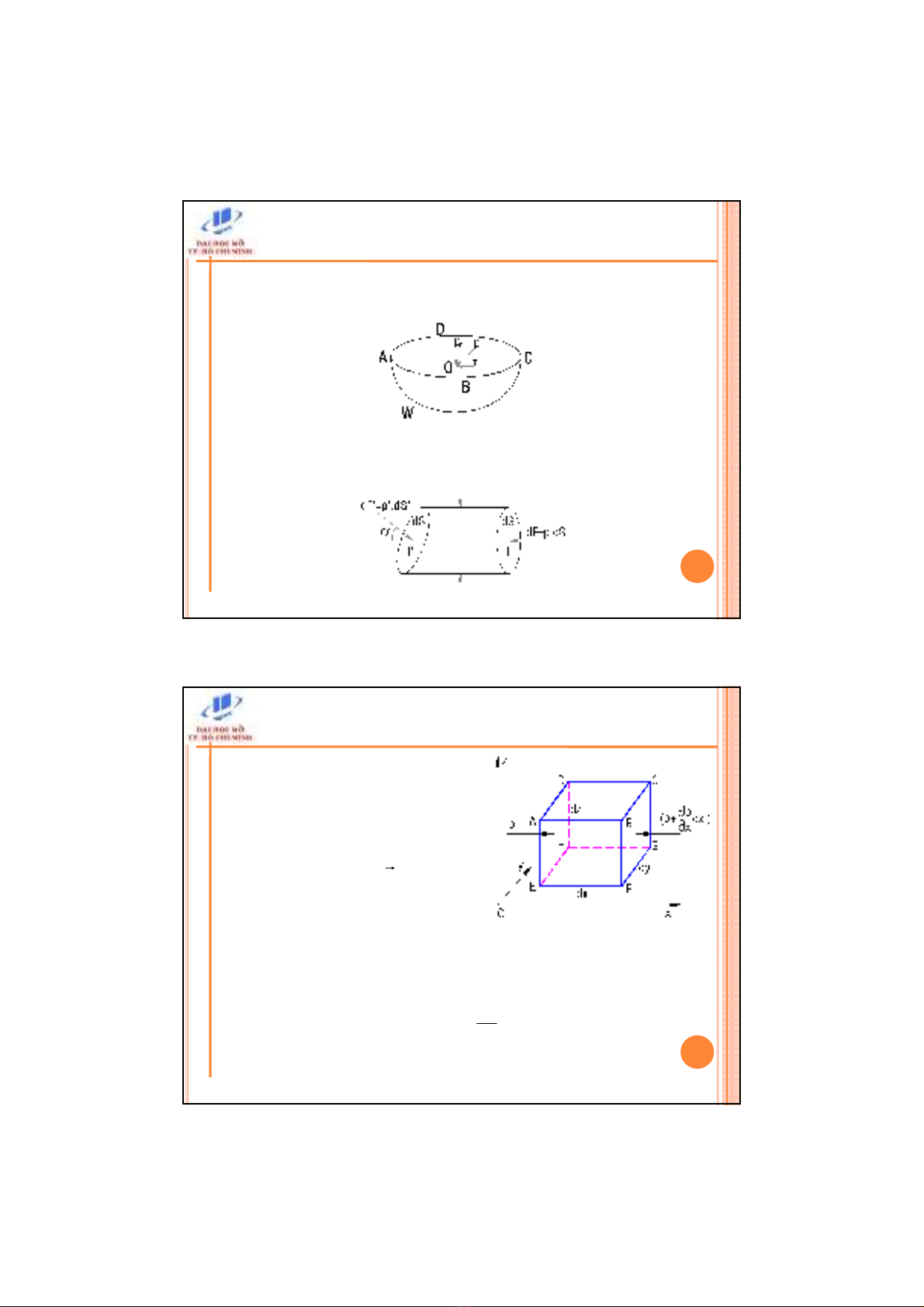
Xét khi cht lng vi phân,
cnh dx,dy,dz, ñng cân bng,
khi lưng riêng ρ
Th.S Bùi Anh Kit
CA CHT LNG CÂN BNG
Lc khiñơn v:
Lc tác dng lên khi hình hp theo phương x:
- Lc khi:
- Lc mt:
dy.dzdx
x
p
pp.dy.dz
∂
∂
+−
x
.Fρ.dx.dy.dz
(
)
zyx F,F,FF
7/26/2012
4
Th.S Bùi Anh Kit
ði u kin cân bng theo phương x:
Phương trình vi phân cơbn
( Phương trình Euler)
0.Fρ.dx.dy.dzdy.dzdx
x
p
pp.dy.dz
x
=+
∂
∂
+−
(1) 0
x
p
ρ
1
F
x
=
∂
∂
−
Rút gn ta ñưc:
phương y
(2) 0
y
p
ρ
1
F
y
=
∂
∂
−
(3) 0
z
p
ρ
1
F
z
=
∂
∂
−
phương z
Vit dưi dng vector:
0pgrad
ρ
1
F=−
3. PHƯƠNG TRÌNH VI PHÂN CƠBN
CA CHT LNG CÂN BNG
PHƯƠNG TRÌNH VI PHÂN MTðNG ÁP
Th.S Bùi Anh Kit
Nhân ln lưt các phương trình (1),(2),(3) vi dx, dy, dz r!i
cng vtheo v:
( )
0dz
z
p
dy
y
p
dx
x
p
ρ
1
dzFdyFdxF zyx =
∂
∂
+
∂
∂
+
∂
∂
−++
Mtñng áp: áp sut thutĩnh ti miñim trên mtñóñ u
bng nhau →p=const →dp=0
Phương trình vi phân mtñng áp:
Tính cht: - Hai mtñng áp khác nhau không thct nhau
- Lc khi tác dng thng góc vi mtñng áp
0dzFdyFdxF
zyx
=++
(
)
0dp
ρ
1
dzFdyFdxF
zyx
=−++
(
)
4
(
)
dzFdyFdxFρdp
zyx
7/26/2012
5
4. PHƯƠNG TRÌNH CƠBN THUTĨNH HC
Dưi"nh hư#ng trng lclc khi theo t$ng phương s%là:
Th.S Bùi Anh Kit
gF 0;F 0;F
zyx
−===
∫
∫
−= dzρgdp
C ρ.g.zp
+
−
=
Tích phân phương trình (5):
Thay vào phương trình (3):
0
z
p
ρ
1
g=
∂
∂
−− (5) ρg
z
p−=
∂
∂
→
→
const
ρ.g.z
p
=
+
)6(
hay:
const
γ
p
z=+ )7(
Phương trình thutĩnh

Th.S Bùi Anh Kit
Áp dng cho 2 ñim A và B:
Nh'n xét:
-Áp sut ti nhng ñim có cùng ñ sâu trong cht lng trng
lcñng cân bng thì bng nhau.
-ð chênh áp sut gia 2 ñim bt kỳtrong cùng mt cht lng
chphthuc vào khong cách thng ñng gia 2 ñimy.
Nu có nhiu loi cht lng khác nhau, không trn ln vào
nhau thì mt phân chia là các mtñng áp nm ngang.
BBAA
ρ.g.zp ρ.g.zp +=+
)zγ(zp p
BAAB
−+=
γhp p
AB
+=
4. PHƯƠNG TRÌNH CƠBN THUTĨNH HC