§5. Phương trình vi phân chuyển động của vật rắn phẳng
Nội dung
1Mở đầu về các hệ cơ học
2Định lý biến thiên động lượng
3Mômen quán tính khối của vật rắn
4Định lý biến thiên mômen động lượng
5Phương trình vi phân chuyển động của vật rắn phẳng
Thiết lập PTVPCĐ của vật rắn phẳng
Thí dụ áp dụng
Cơ học kỹ thuật (ME3010) Chương 2. Các phương pháp động lượng 2014 52 / 64
§5. Phương trình vi phân chuyển động của vật rắn phẳng Thiết lập PTVPCĐ của vật rắn phẳng
Nội dung
1Mở đầu về các hệ cơ học
2Định lý biến thiên động lượng
3Mômen quán tính khối của vật rắn
4Định lý biến thiên mômen động lượng
5Phương trình vi phân chuyển động của vật rắn phẳng
Thiết lập PTVPCĐ của vật rắn phẳng
Thí dụ áp dụng
Cơ học kỹ thuật (ME3010) Chương 2. Các phương pháp động lượng 2014 52 / 64
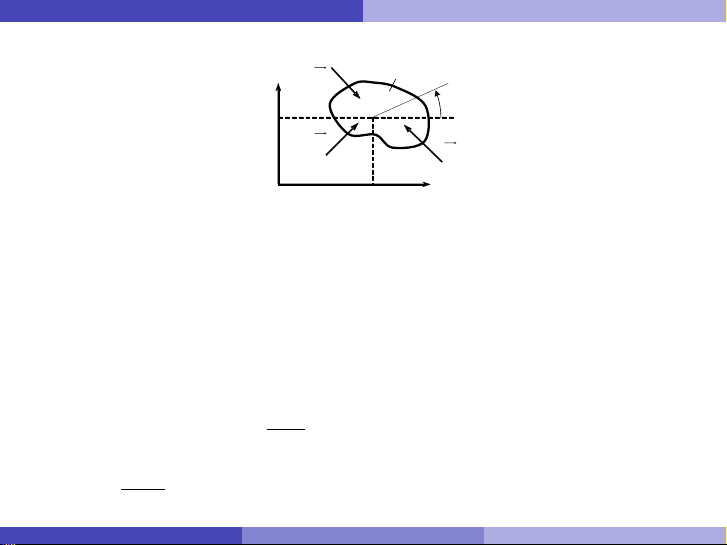
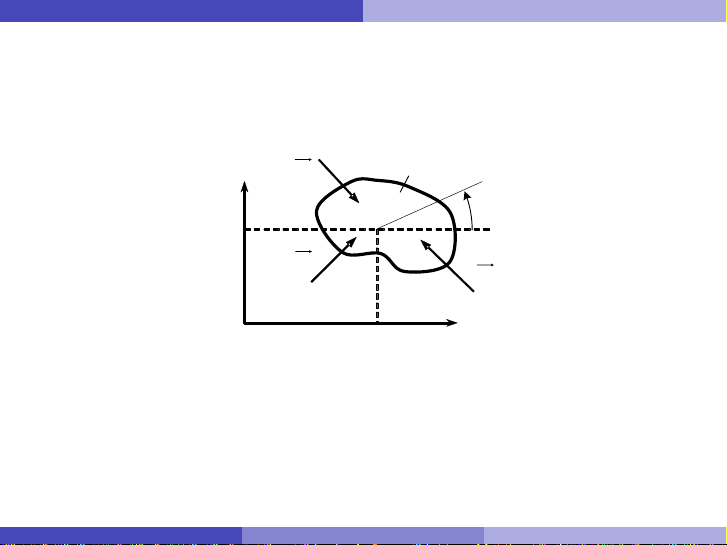
§5. Phương trình vi phân chuyển động của vật rắn phẳng Thiết lập PTVPCĐ của vật rắn phẳng
Thiết lập phương trình
Xét hình phẳng Snhư hình vẽ.
C
y
yC
xCx
ϕ
2
F
n
F
1
F
O
S
Cơ học kỹ thuật (ME3010) Chương 2. Các phương pháp động lượng 2014 53 / 64
§5. Phương trình vi phân chuyển động của vật rắn phẳng Thiết lập PTVPCĐ của vật rắn phẳng
C
y
yC
xCx
ϕ
2
F
n
F
1
F
O
S
Áp dụng định lý chuyển động khối tâm
m~
aC=X~
Fe
k⇒(m¨xC=PFe
kx
m¨yC=PFe
ky
(57)
Áp dụng định lý biến thiên mômen động lượng
d~
LC
dt =X~
mC~
Fe
k(58)
dLCz
dt =XmCz ~
Fe
k⇒JCz ¨ϕ=XmCz ~
Fe
k(59)
Cơ học kỹ thuật (ME3010) Chương 2. Các phương pháp động lượng 2014 54 / 64
§5. Phương trình vi phân chuyển động của vật rắn phẳng Thiết lập PTVPCĐ của vật rắn phẳng
(Do LCz =JCz ω=JCz ˙ϕ). Kết hợp các phương trình (57) và (59):
m¨xC=PFe
kx
m¨yC=PFe
ky
JCz ¨ϕ=PmCz ~
Fe
k(60)
Cơ học kỹ thuật (ME3010) Chương 2. Các phương pháp động lượng 2014 55 / 64