
10/ 24/ 2012
1
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
Tính bền thanh
khi ứng suất không đổi
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
5.1.1. Khái niệm
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
Trong chương này chỉ xét ứng suất là hằng số (không
thay đổi theo thời gian, nhiệt độ, sự hoạt động của chi
tiết máy…)
- Là tính toán thanh đảm bảo điều kiện bền.
- Tính mức độ chịu lực thanh sao cho thanh không bị phá
vỡ khi làm việc
max ; max
5.1.1. Khái niệm
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
5.1.2. Quan niệm bài toán phẳng

10/ 24/ 2012
2
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
5.1.3. Phân loại các trường hợp chịu lực của thanh
a. Trường hợp chịu lực đơn giản
Khi trên mặt cắt của thanh chỉ có một thành phần nội lực
1. (lực dọc trục): thanh chịu
kéo nén đúng tâm
z
N
2. (lực cắt): thanh chịu cắt
y
Q
3. (moment uốn): thanh
chịu uốn thuần túy
x
M
4. (moment xoắn): thanh
chịu xoắn thuần túy
z
M
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
5.1.3. Phân loại các trường hợp chịu lực của thanh
a. Trường hợp chịu lực đơn giản
1. (lực dọc trục): thanh chịu kéo nén đúng tâm
z
N
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
5.1.3. Phân loại các trường hợp chịu lực của thanh
a. Trường hợp chịu lực đơn giản
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
5.1.3. Phân loại các trường hợp chịu lực của thanh
a. Trường hợp chịu lực đơn giản
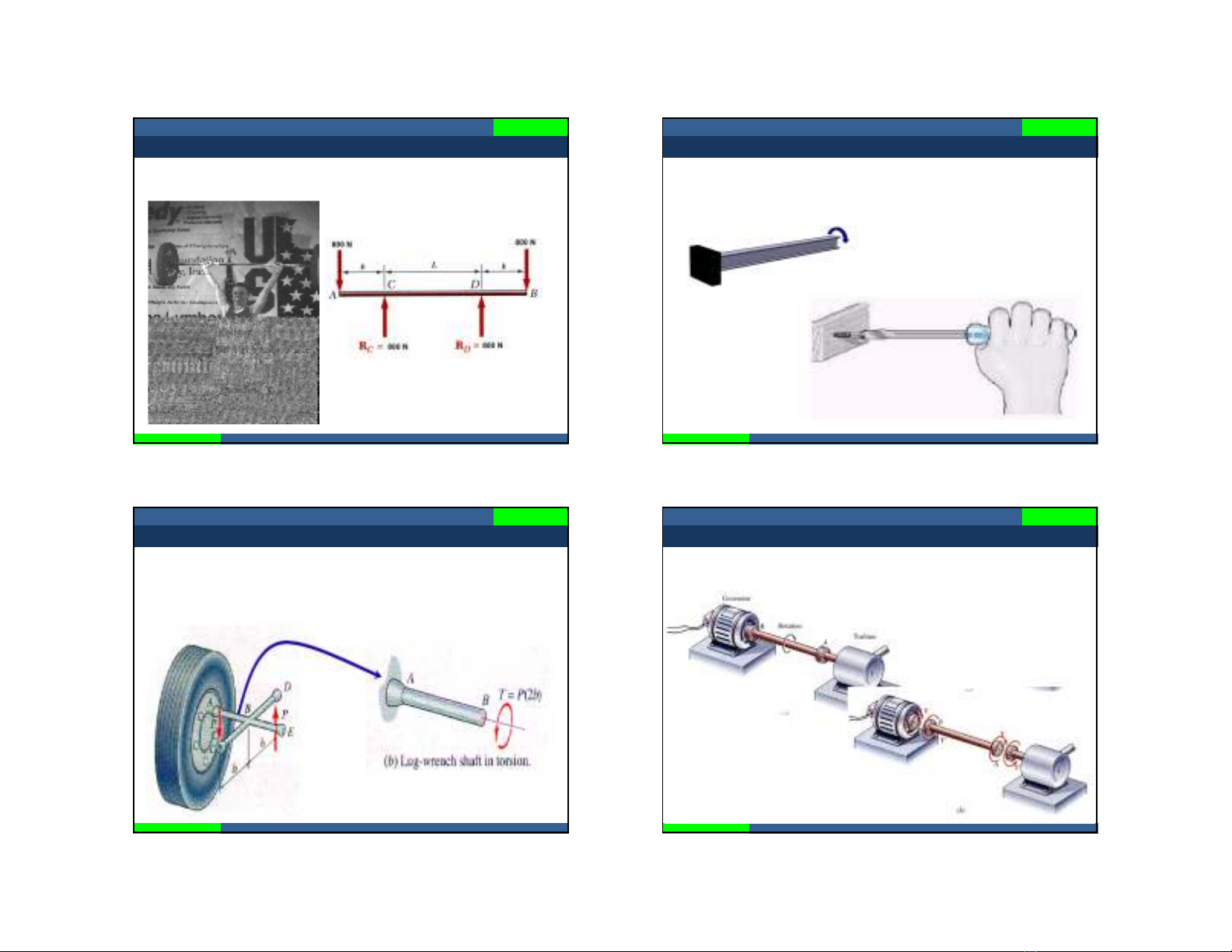
2. (moment uốn): thanh chịu uốn thuần túy
x
M
10/ 24/ 2012
3
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
5.1.3. Phân loại các trường hợp chịu lực của thanh
a. Trường hợp chịu lực đơn giản
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
5.1.3. Phân loại các trường hợp chịu lực của thanh
a. Trường hợp chịu lực đơn giản
3. (moment xoắn): thanh chịu xoắn thuần túy
z
M
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
5.1.3. Phân loại các trường hợp chịu lực của thanh
a. Trường hợp chịu lực đơn giản
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
5.1.3. Phân loại các trường hợp chịu lực của thanh
a. Trường hợp chịu lực đơn giản
10/ 24/ 2012
4
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.1. Khái niệm
5.1.3. Phân loại các trường hợp chịu lực của thanh
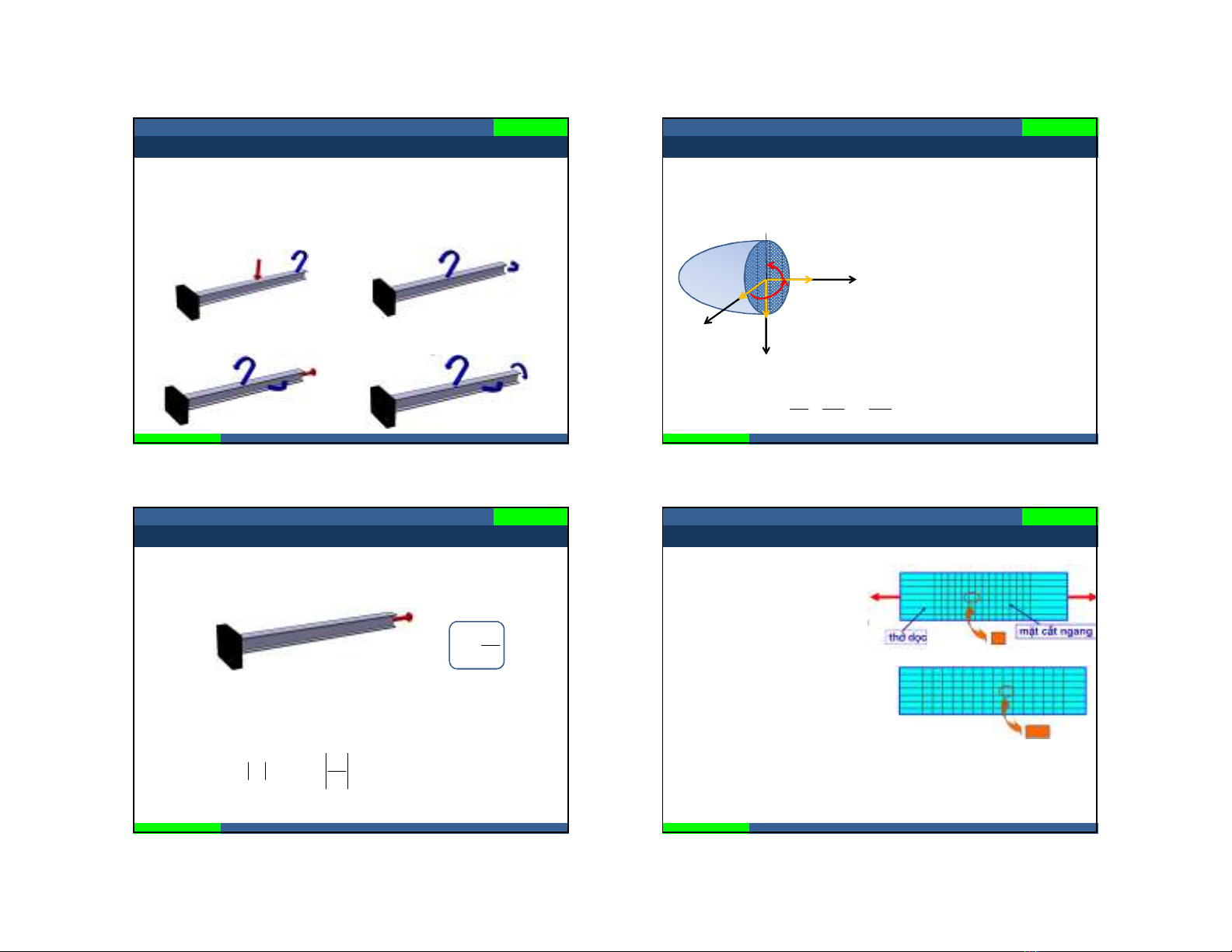
b. Trường hợp chịu lực phức tạp
Khi trên mặt cắt của thanh chỉ có từ hai thành phần nội lực trở lên
1. : thanh chịu uốn ngang
phẳng
,
y x
Q M
2. : thanh chịu uốn xiên
,
x y
M M
3. : thanh
chịu uốn và kéo nén đồng thời
, ,
x y z
M M N
4. : thanh chịu uốn
và xoắn đồng thời
, ,
x y z
MMM
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.2. Thiết lập công thức tính ứng suất pháp tổng quát
z z
F
x z
F
y z
F
N dF
M ydF
M xdF
Giả sử xét 1 thanh chịu lực sao cho trên mặt cắt ngang của
thanh có các thành phần nội lực liên hệ với ứng
suất pháp bằng các biểu thức:
z
, ,
z x y
N M M
z
N
O
z
x
y
x
M
y
M
y
Q
x
Q
Từ định luật Hooke ta chứng minh được công thức:
z z
E
(*)
y
z x
z
x y
M
N M y x
F J J
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.3. Tính bền khi thanh chịu kéo nén đúng tâm
z
z
N
F
Khi thanh chịu kéo nén đúng tâm, trên mặt cắt ngang chỉ có
thành phần
z
Ứng suất pháp phân bố đều trên mặt cắt ngang của thanh
Điều kiện bền của thanh:
max max z
z
N
F
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
5.3. Tính bền khi thanh chịu kéo nén đúng tâm
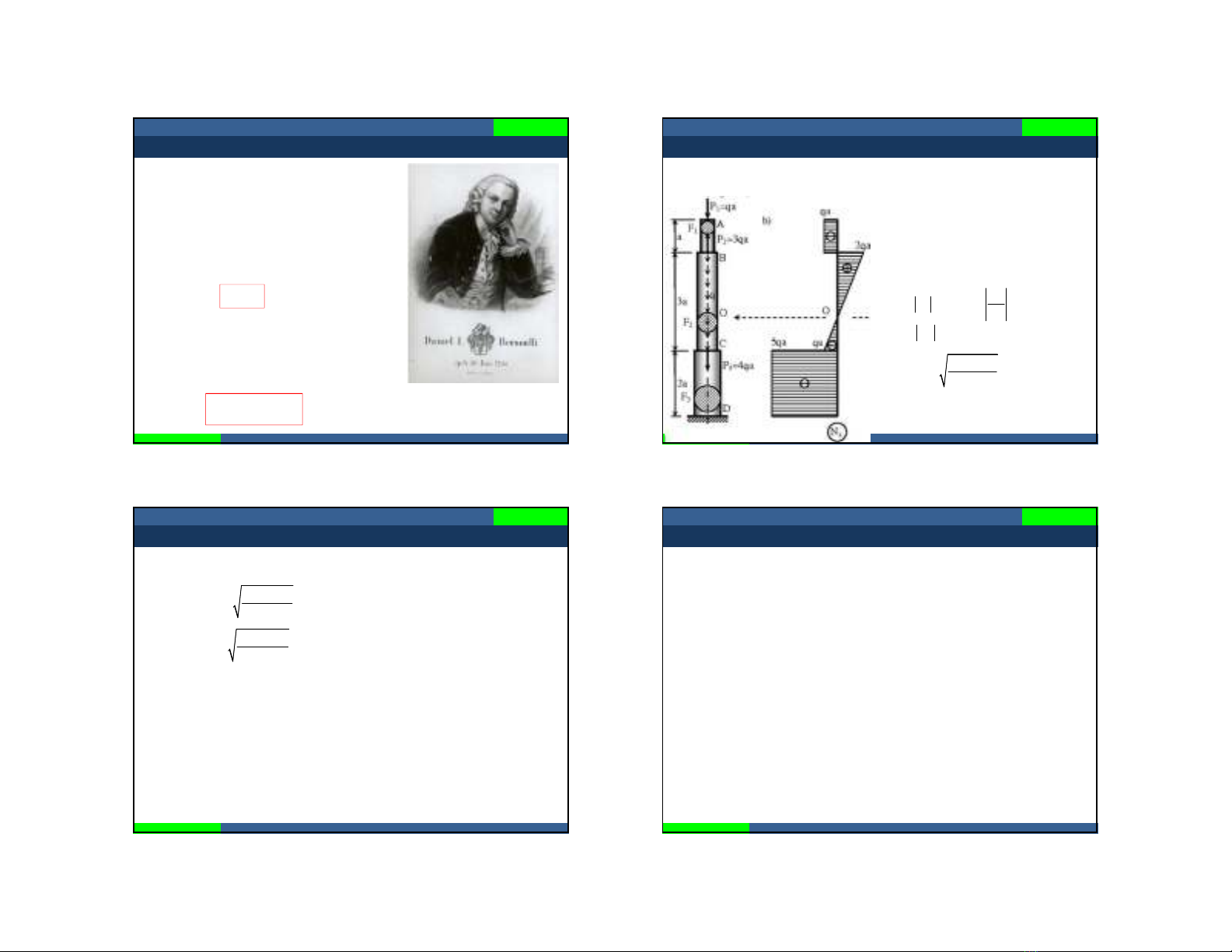
Thí nghiệm
Vạch trên bề mặt ngoài:
-Hệ những đường thẳng song
song trục thanh.
-Hệ những đường thẳng vuông
góc trục thanh.
Sau biến dạng:
-Những đường thẳng song song
trục thanh vẫn song song trục
thanh.
-Những đường thẳng vuông góc
trục thanh vẫn vuông góc trục
thanh.
10/ 24/ 2012
5
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
Giả thiết
a. Giả thiết về mặt cắt ngang phẳng:
Trong quá trình biến dạng, các mặt cắt
ngang luôn phẳng và vuông góc với
trục thanh. Không có ứng suất tiếp
trên mặt cắt ngang.
b. Giả thiết về các thớ dọc:
Trong quá trình biến dạng, các thớ
dọc không xô đẩy lẫn nhau (không
tác dụng tương hỗ lẫn nhau).
5.3. Tính bền khi thanh chịu kéo nén đúng tâm
0
0
x y
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
Câu hỏi 1: Cho q = 10 KN/cm.
Hỏi đường kính cho các đoạn
trục là bao nhiêu thì đảm bảo chi
tiết không bị hư hỏng ?
Biết a = 50cm; vật liệu bằng thép
có:
2
12 /
kN cm
max max z
z
N
F
Đoạn AB
/ 10 50 /12 41.67
z
F N
1
41.67 4
7.28
D cm
Chọn D1 = 10cm
Ví dụ:
5.3. Tính bền khi thanh chịu kéo nén đúng tâm
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
Tương tự cho đoạn BC và CD:
2
12000 4
10.3
D cm
3
30000 4
16.29
D cm
Ta chọn D2 = 15cm; D3 = 20cm
* Câu hỏi 2: cho D1 = 50cm, D2 = 75cm; D3 = 100cm; Hỏi tải trọng lớn
nhất có thể đặt vào chi tiết là bao nhiểu ?
* Câu hỏi 3: cho D1 = 15cm, D2 = 30cm; D3 = 50cm; q = 13kN/cm Hỏi chi
tiết có bền không ?
5.3. Tính bền khi thanh chịu kéo nén đúng tâm
Chương V: Tính bền thanh khi ứng suất không đổi
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
Ghi chú
Ba dạng bài toán tính bền
1. Bài toán kiểm tra bền
- Kiểm tra lớp biên trước
- Kiểm tra lớp trung hòa
- Kiểm tra lớp trung gian (nếu là mặt cắt định hình I, T, L, U...)
2. Bài toán xác định kích thước mặt cắt ngang
- Dựa vào lớp biên để tính sơ bộ kích thước mặt cắt ngang
- Kiểm tra bền lớp trung hòa
- Kiểm tra lớp trung gian (nếu là mặt cắt định hình I, T, L, U...)
3. Bài toán xác định tải trọng cho phép
Tương tự dạng 2






















![Bài giảng Kỹ thuật robot [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250715/vijiraiya/135x160/366_bai-giang-ky-thuat-robot.jpg)
![Câu hỏi ôn tập Cơ sở xử lý ảnh số [năm] chuẩn nhất](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250710/kimphuong1001/135x160/84701752136985.jpg)

![Câu hỏi ôn tập Robot công nghiệp [năm hiện tại]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250702/kimphuong555/135x160/7711751422232.jpg)
