17/09/201414
1
Chương III
Ứng suất và Biến dạng
Chương III: Ứng suất và biến dạng
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
3.1. Ứng suất
3.2. Trạng thái ứng suất.
3.3. Trạng thái ứng suất phẳng
3.4. TTƯS trong bài toán phẳng – P.P đồ thị
3.5. Biến dạng
3.6. Liên hệ giữa ứng suất và Biến dạng
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
3.1.1. Khái niệm
3.1. Ứng suất
Chia vật bằng một mặt cắt và khảo sát tính chất của các lực tiếp xúc
truyền qua mặt này do phần tách ra tác động lên. Các lực tiếp xúc
phân bố khắp mặt cắt với chiếu và giá trị thay đổi, chúng được gọi là
ứng suất (hay ứng lực, sức căng) tại một điểm.
(I)
B
p
B
B
p
(II)
Ứng suất
Ứng suất: nội lực tại điểm
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
Xét một điểm M trên mặt cắt và một phân tố điện tích chung quanh
M: dF. Nếu gọi ứng lực trên dF là
thì ứng suất
tại M trên mặt
phẳng vuông góc Oz là:
dP
p
dF
Khi dF
0
3.1.1. Khái niệm
3.1. Ứng suất
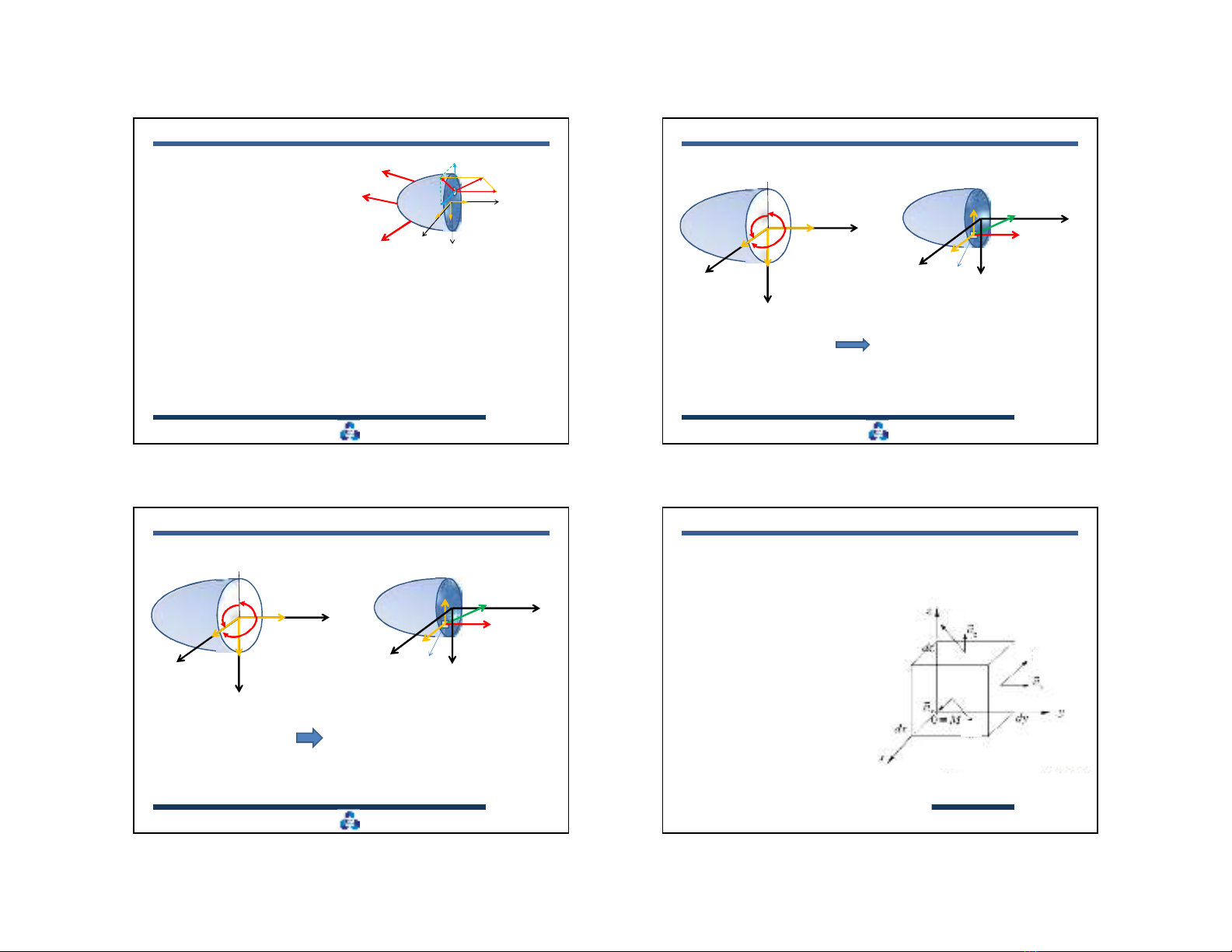
Ứng suất
được phân
thành 2 thành phần:
: Ứng suất pháp hướng theo pháp tuyến mặt cắt
: Ứng suất tiếp nằm trong mặt cắt
1
P
2
P
3
P
dP
x
M
y
z
dF
p
O
j
k
i
* Ứng suất pháp: gây ra biến dạng dài
* Ứng suất tiếp: gây ra biến dạng góc
17/09/201414
2
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
z zy zx
p k j i
Trong hệ trục Cartesian
như hình vẽ:
* Ứng suất pháp: hướng theo phương z
* Ứng suất tiếp: hướng theo phương x
* Ứng suất tiếp: hướng theo phương y
z
zx
zy
3.1.1. Khái niệm
3.1. Ứng suất
1
P
2
P
3
P
x
M
y
z
p
O
j
k
i
z
zy
zx
Qui ước dấu của các thành phần ứng suất:
- Ứng suất pháp xem là dương khi vector biểu diễn nó cùng
chiều với pháp tuyến ngoài của mặt cắt.
- Ứng suất tiếp là dương khi vector biểu diễn nó cùng chiều
Ox, Oy.
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
z z
F
y zy
F
x zx
F
N dF
Q dF
Q dF
z
M
z
N
C
z
x
y
x
M
y
M
y
Q
x
Q
p
( )
A
zy
z
O
zx
z
x
y
.
F
R p dF
dF
3.1.2. Quan hệ Nội lực - Ứng suất
3.1. Ứng suất
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
( )
x z
F
y z
F
z zx zy
F
M ydF
M xdF
M y x dF
.
C C
F
M m p dF
z
M
z
N
C
z
x
y
x
M
y
M
y
Q
x
Q
p
( )
A
zy
z
O
zx
z
x
y
dF
3.1.2. Quan hệ Nội lực - Ứng suất
3.1. Ứng suất
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
z
p
y
p
x
p
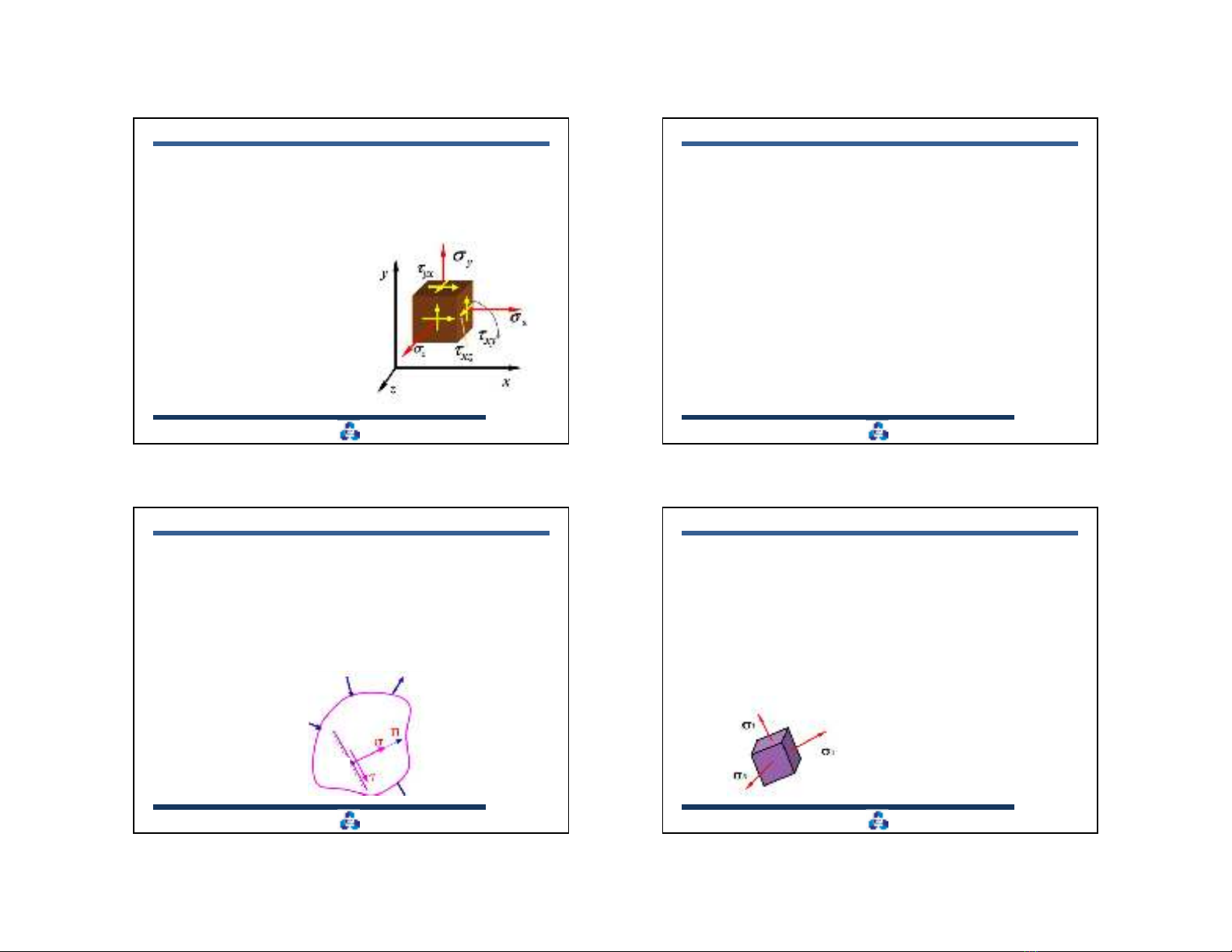
3.1.3. Các thành phần ứng suất
Tổng quát: Tách một phân tố tại C bằng 6 mặt vi phân trực giao
với các trục tọa độ.
Trên 3 mặt vi phân dương có các
vector ứng suất:
Mỗi vector trong chúng có ba
thành phần song song với ba
trục tọa độ:
, ,
x y z
p p p
, ,
, ,
, ,
x x xy xz
y y yx yz
z z zx zy
p
p
p
3.1. Ứng suất
17/09/201414
3
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
Ứng suất tại một điểm được đặc trưng bởi chín thành phần ứng
suất và chúng được viết dưới dạng Tensor:
x xy xz
yx y yz
zx zy z
T
3.1.3. Các thành phần ứng suất
3.1. Ứng suất
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
* Nguyên lý tương hỗ ứng suất tiếp
Trên hai mặt vi phân trực giao, các thành phần ứng suất vuông
góc với cạnh chung thì bằng nhau và có chiều cùng hướng vào
hoặc hướng ra cạnh chung đó.
; ;
xy yx xz zx yz zy
x xy xz
y yz
z
T
Sym
Khi đó tensor ứng suất là một tensor đối xứng, do đó trạng
thái ứng suất chỉ còn phụ thuộc 6 thông số:
3.1.3. Các thành phần ứng suất
3.1. Ứng suất
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
3.2. Trạng thái ứng suất.
3.2.1. Trạng thái ứng suất tại một điểm
Nếu cho qua M những mặt cắt π khác nhau, thì tương ứng với
mỗi vị trí của π ta được 1 vector ứng suất. Tập hợp tất cả các
vector ứng suất này được gọi là trạng thái ứng suất tại M. Tập
hợp này không phải là một tập hợp vector độc lập.
M
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
3.2.2. Phương chính và ứng suất chính
Mặt chính: mặt cắt mà trên đó phương của trùng với phương của
p
n
n
Khi đó: - Phương của được gọi là phương chính
- Ứng suất được gọi là ứng suất chính
n
Tại mỗi điểm của vật thể đàn hồi ta luôn tìm được ba phương
chính vuông góc nhau từng đôi một. Ứng với ba phương chính
ta có ba ứng suất chính:
1 2 3
Các ứng suất chính
này không phụ thuộc
việc chọn hệ trục tọa
độ
3.2. Trạng thái ứng suất.
17/09/201414
4
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
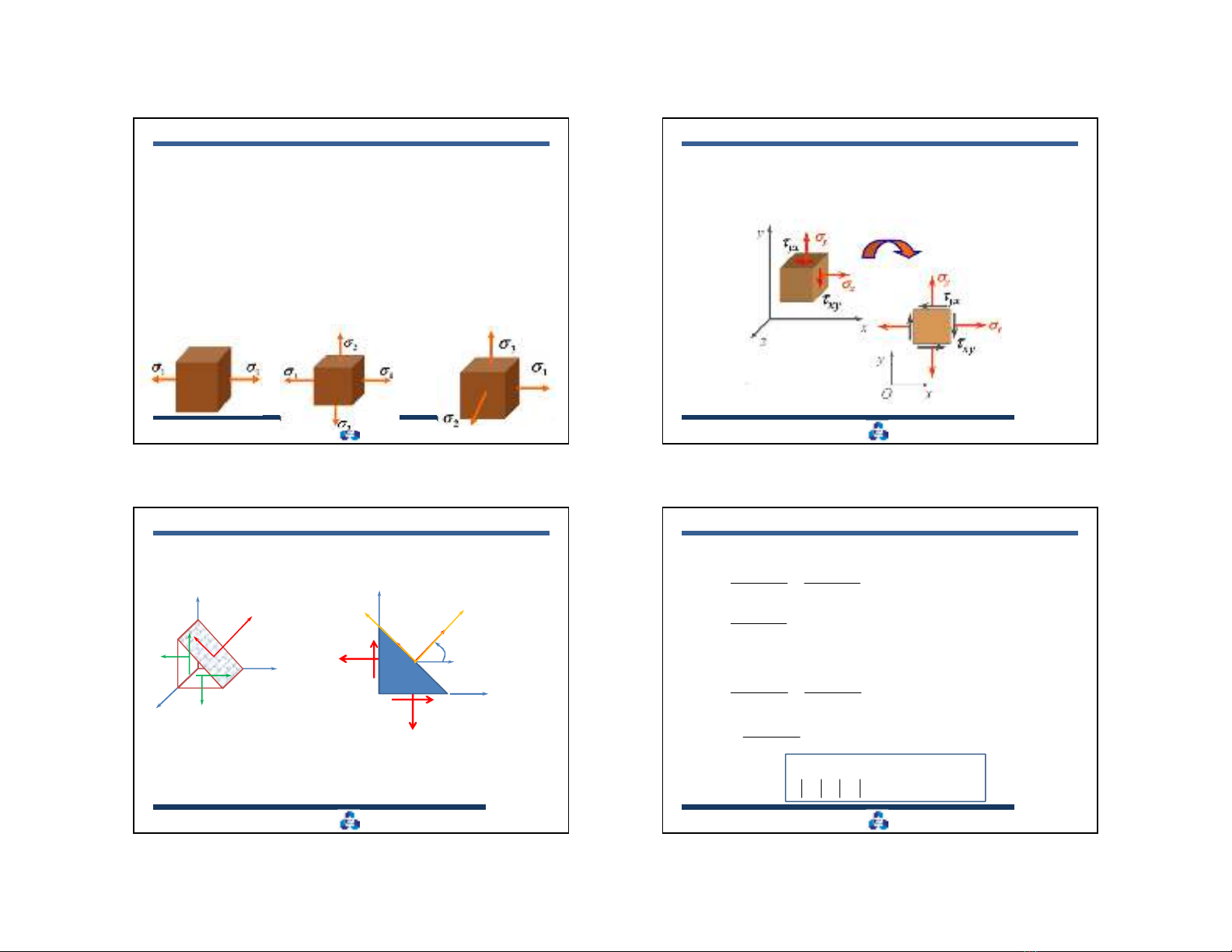
3.2.3. Các trạng thái ứng suất
Nếu ta chọn hệ trục tọa độ sao cho ba trục trùng với ba phương
chính:
1
2
3
0 0
0 0
0 0
T
Trạng thái ứng suất
khối: ba ứng suất
chính đều khác không
Trạng thái ứng suất
phẳng: có một ứng suất
chính bằng không.
Trạng thái ứng suất
đơn: có hai ứng suất
chính bằng không.
3.2. Trạng thái ứng suất.
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
3.3. Trạng thái ứng suất phẳng
Là trạng thái của điểm có vector ứng suất tổng luôn nằm trong
một mặt phẳng, với mọi mặt vi phân khảo sát.
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
3.3.1. Ứng suất trên mặt cắt nghiêng bất kỳ (//z)
3.3. Trạng thái ứng suất phẳng
x
y
z
x
xy
y
yx
u
v
y
yx
y
x
x
xy
u
v
x
u
uv
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
cos 2 s in2
2 2
x y x y
u xy
s in2 cos 2
2
x y
uv xy
Tại mặt vuông góc với mặt có pháp tuyến u ( )
0
90
cos 2 s in2
2 2
x y x y
v xy
s in2 cos 2
2
x y
vu xy
Nhận xét:
u v x y
const
uv vu
Ứng suất pháp và tiếp trên mặt nghiêng:
(3.10)
17/09/201414
5
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
3.3.2. Ứng suất chính – Phương chính
Mặt chính là mặt có ứng suất tiếp bằng không. Để tìm mặt chính:
0
uv
0 0
s in2 cos 2 0
2
x y
uv xy
0
2
2 (*)
xy
x y
tg
Hai trị số khác biệt nhau 90
0
Hai phương chính
0
Thay vào , ta thu được các ứng suất chính
u
2 2
max
min
1
( ) 4 (**)
2 2
x y
x y xy
1
0
2
tan /2
2
xy
x y
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
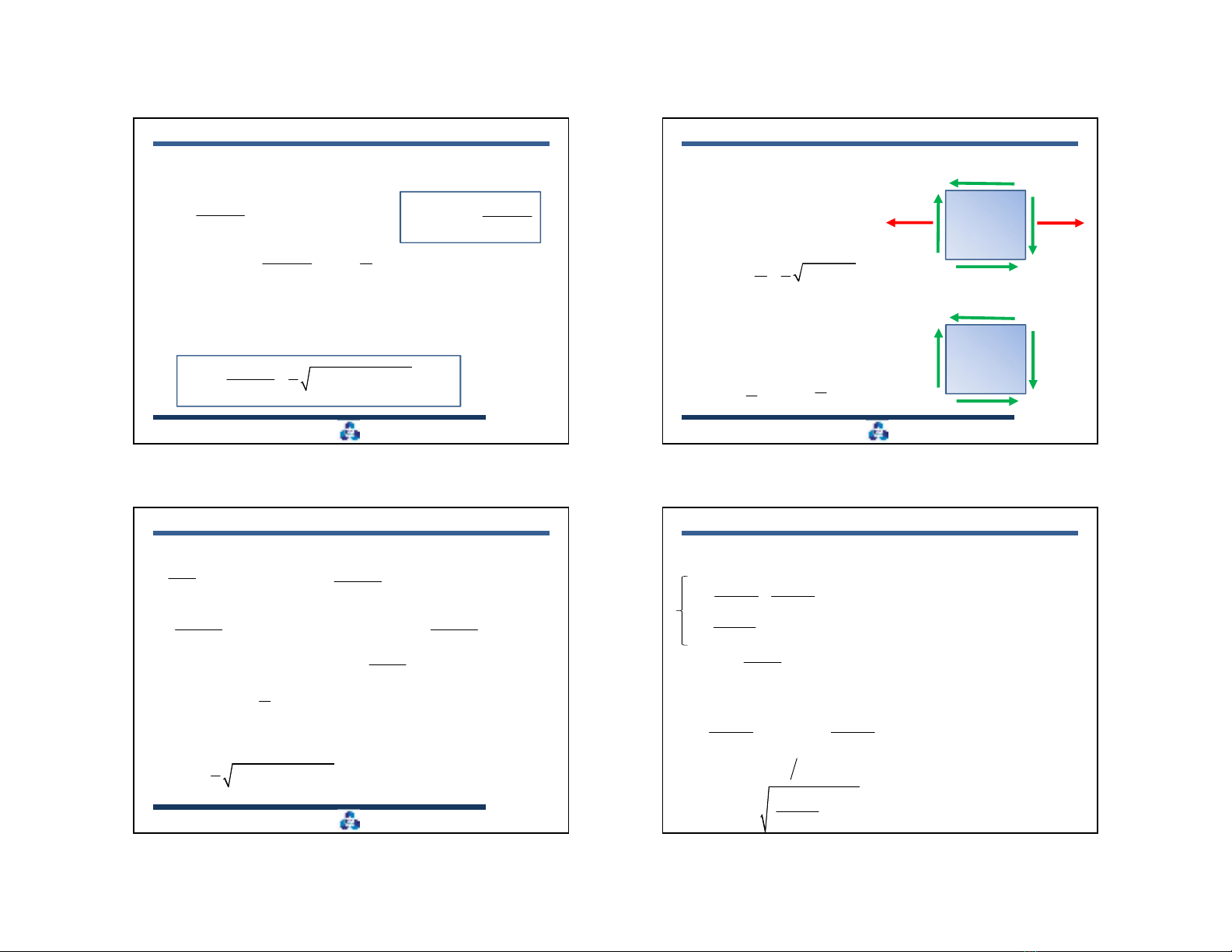
** Hai trường hợp đặc biệt
a. Trạng thái ứng suất phẳng đặc biệt
; 0;
x y xy
2 2
max
min
1
4
2 2
Thay vào (**) ta được:
b. Trạng thái ứng suất trượt thuần túy
0;
x y xy
max 1 3
min
hay
Thay vào (**) ta được:
1
4
2
4
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
3.3.3. Ứng suất tiếp cực trị
0
uv
d
d
2 cos 2 2 sin 2 2
2 2
x y x y
xy
xy
tg
So sánh với (*), ta được:
0
1
2
2
tg tg
0
4
Mặt có ưs tiếp cực trị tạo với
mặt chính một góc 45
0
s in2 cos 2
2
x y
uv xy
Thay vào ta được:
uv
2 2
max
min
1
( ) 4
2
x y xy
Chương III. Ứng suất – Biến dạng
HCM 08/2014
Applied Mechanic
Hochiminh city University of Technology
3.4. TTƯS trong bài toán phẳng – P.P đồ thị
cos 2 s in2
2 2
x y x y
u xy
s in2 cos 2
2
x y
uv xy
2 2
2
2
2 2
x y x y
u uv xy
2
x y
Chuyển vế qua trái, bình phương 2 vế, cộng 2 vế cho
2
uv
Ta thu được phương trình vòng tròn Mohr ứng suất
Trục hoành:
Trục tung:
3.4.1. Cơ sở của phương pháp
Tâm:
2;0
x y
Bán kính:
2
2
2
x y
xy
R
Tọa độ các điểm trên vòng tròn Mohr
ứng suất cho ta giá trị các ưs pháp và
ưs tiếp nằm trên những mặt khác nhau
đi qua điểm có trạng thái ưs ta đang xét.


























