Môn học:
CƠ HỌC ỨNG DỤNG
Đề cương môn học:
Chương 1: Những vấn đề cơ bản của tĩnh học vật rắn tuyệt đối
Chương 2: Nội lực và Biểu đồ nội lực
Chương 3: Ứng suất và Biến dạng
Chương 4: Lý thuyết bền
Chương 5: Đặc trưng hình học của mặt cắt ngang
Chương 6: Tính bền thanh khi ứng suất không đổi
Chương 7: Các bộ phận truyền động
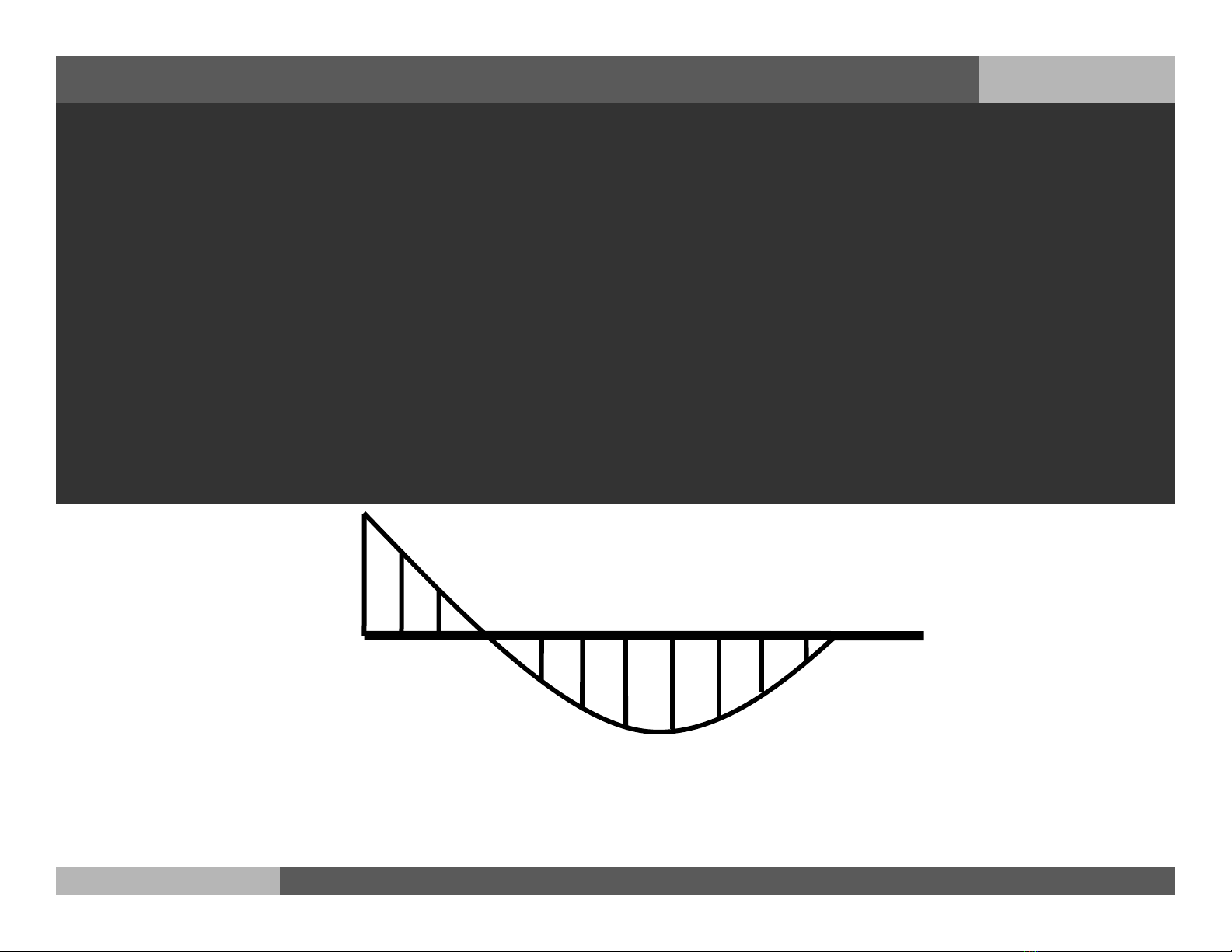
Chương II
Nội lực và Vẽ biểu đồ nội lực
Chương II: Nội lực và Vẽ biểu đồ nội lực
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
Nguyễn Thanh Nhã
Bộ môn Cơ Kỹ Thuật – Khoa Khoa Học Ứng Dụng – 106B4
ĐT: 08.38660568 – 0909568181
Email: thanhnhanguyendem@gmail.com
Chương II: Nội lực và Vẽ biểu đồ nội lực
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
2.1. Các khái niệm cơ bản về Cơ học vật rắn biến dạng
*** Nhiệm vụ và đối tượng ***
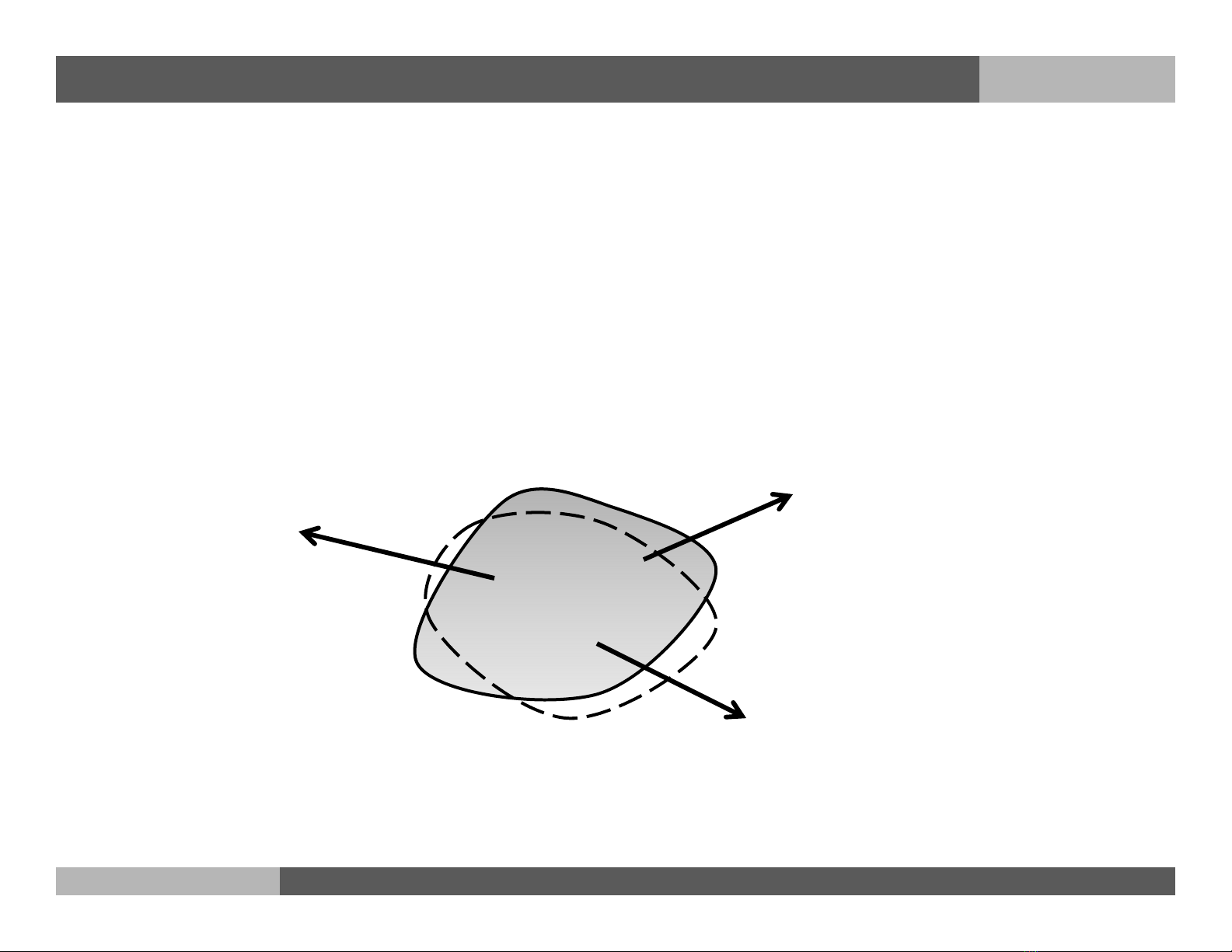
Cơ học vật rắn biến dạng nghiên cứu những dịch chuyển tương đối
giữa các chất điểm thuộc vật rắn khi nó chịu tác dụng bởi hệ lực cân
bằng. Để từ đó ta có thể tính toán sức chịu đựng của vật liệu
P3
P1
P2
Chương II: Nội lực và Vẽ biểu đồ nội lực
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
2.1. Các khái niệm cơ bản về Cơ học vật rắn biến dạng
Mô hình nghiên cứu: Thanh thẳng, Khung
Vật liệu: Đàn hồi _ Liên tục _ Đẳng hướng
*** Nhiệm vụ và đối tượng ***
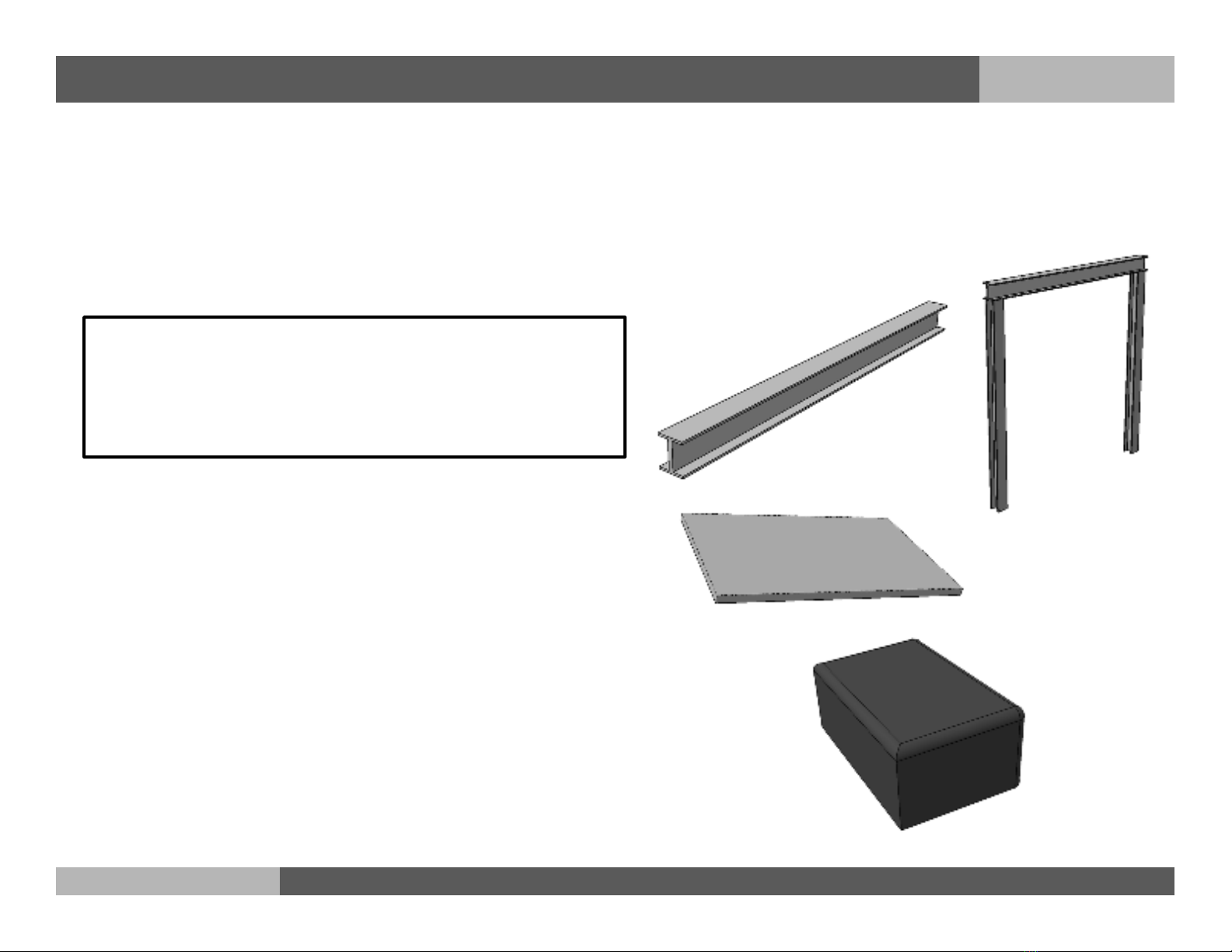
Thanh: vật thể có kích thước 1
phương lớn hơn 2 phương kia
nhiều lần
Tấm vỏ: vật thể có kích thước 2
phương lớn hơn phương còn lại
nhiều lần
Khối: vật thể có kích thước 3
phương tương đương nhau
Mô hình biến dạng bé
Chương II: Nội lực và Vẽ biểu đồ nội lực
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
2.1.1. Nội lực
a. Định nghĩa:
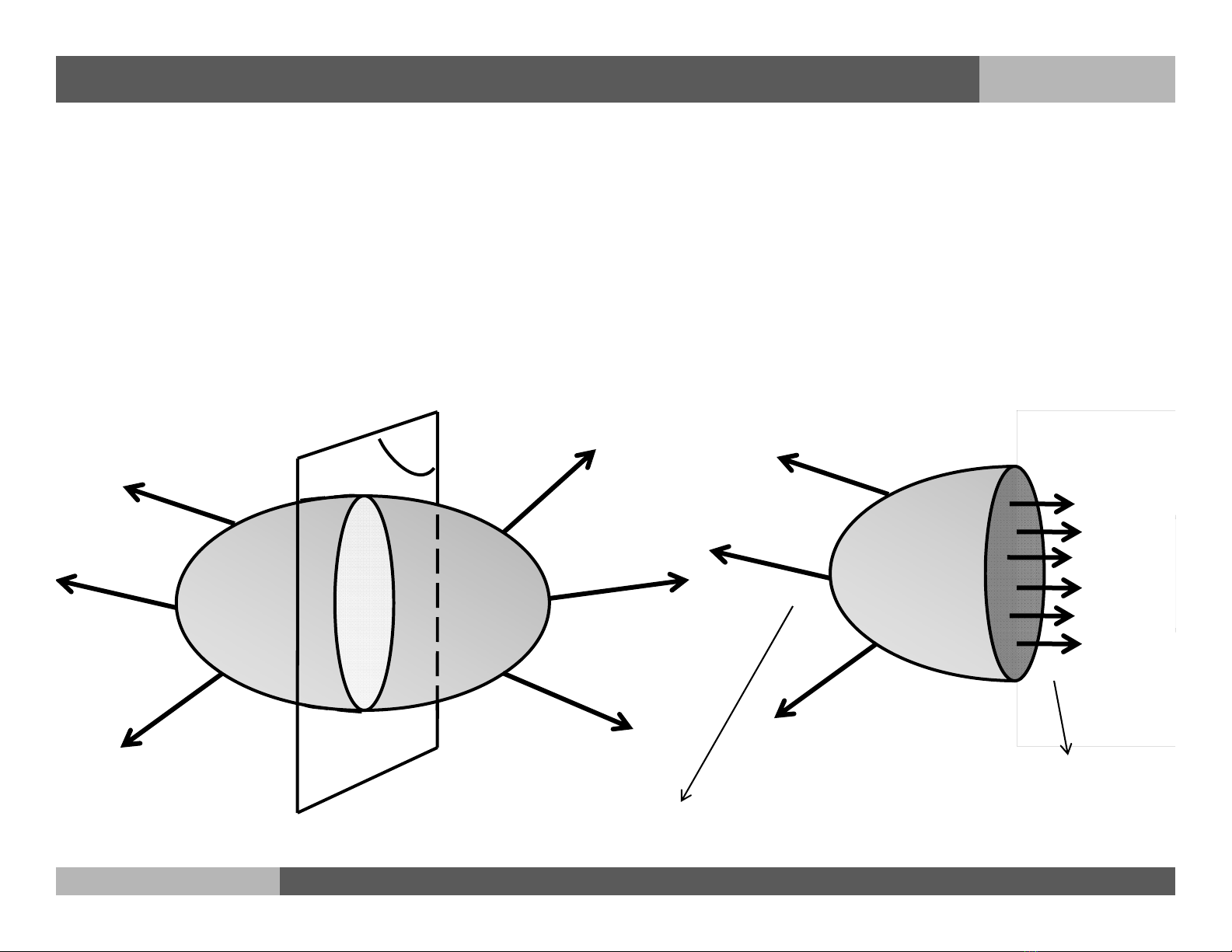
Nội lực là độ tăng của lực liên kết giữa các phân tử thuộc vật rắn khi
vật thể chịu tác dụng của hệ lực cân bằng.
(A) (B)
π
(A)
Ngoại lực
Nội lực
b. Phương pháp khảo sát: Phương pháp mặt cắt ngang