11/21/2012
1
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
Chương VI
Tính biến dạng thanh
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.1. Khái niệm
Đối với vật thể dạng thanh, biến dạng gồm 3 loại:
6.1.1. Khái niệm
-Biến dạng xoắn: còn gọi là góc xoắn, do Mzgây ra.
l
Biến dạng dài
l
-Biến dạng dài: do thành phần nội lực dọc trục Nzgây ra.
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
x
y
z
a
a’
Góc xoay quanh trục x
Độ võng y
-Độ võng, góc xoay: do các thành phần moment uốn gây ra.
6.1. Khái niệm
6.1.1. Khái niệm
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.1. Khái niệm
6.1.2. Các phương pháp tính
- Phương pháp tích phân phương trình vi phân: Dựa vào các
phương trình vi phân biểu diễn mối quan hệ giữa chuyển vị với
ứng suất , đặc trưng hình học tiết diện và tính chất cơ học của
vật liệu thanh.
- Phương pháp năng lượng: Dựa vào quan hệ năng lượng
giữa công của ngoại lực và năng lượng tích lũy trong thanh khi
thanh biến dạng.
Nhận xét: Phương pháp năng lượng dễ sử dụng hơn nhiều
khi dùng cho các bài toán phức tạp khác nhau, vì vậy
phương pháp này được cho là phương pháp vạn năng,
được sử dụng phổ biến hơn.
11/21/2012
2
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.2. Phương pháp tích phân phương trình vi phân
6.2.1. Phương pháp tích phân trực tiếp
6.2.1.1. Các phương trình cơ bản
Để tính biến dạng dài, biến dạng xoắn, góc xoay ta sử dụng
các phương trình vi phân sau:
z
z
z
x x
x
N
dl
dz EA
M
d
dz GJ
d M
dz EJ
z
z z
x
x x
dl
N EA
dz
d
M GJ
dz
d
M EJ
dz
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.2. Phương pháp tích phân phương trình vi phân
6.2.1. Phương pháp tích phân trực tiếp
6.2.1.2. Thanh chịu kéo nén đúng tâm
Trên mặt cắt ngang thanh chịu kéo nén đúng tâm chỉ có thành
phần lực dọc Nz, nên trong trường hợp này thanh chỉ có biến
dạng dài:
z
N
dl
dz EA
z
l
N
dl dz
EA
a. Nếu , ,
z
N const A const E const
0
.
l
z z
N N
l dz l
EA EA
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.2. Phương pháp tích phân phương trình vi phân
6.2.1. Phương pháp tích phân trực tiếp
b. Nếu , ta chia thanh thành n
đoạn sao cho trên mỗi đoạn 3 đại lượng này đều là hằng số.
, ,
z
N const F const E const
1
.
n
zi
i
i
i i
N
l l
E A
6.2.1.2. Thanh chịu kéo nén đúng tâm
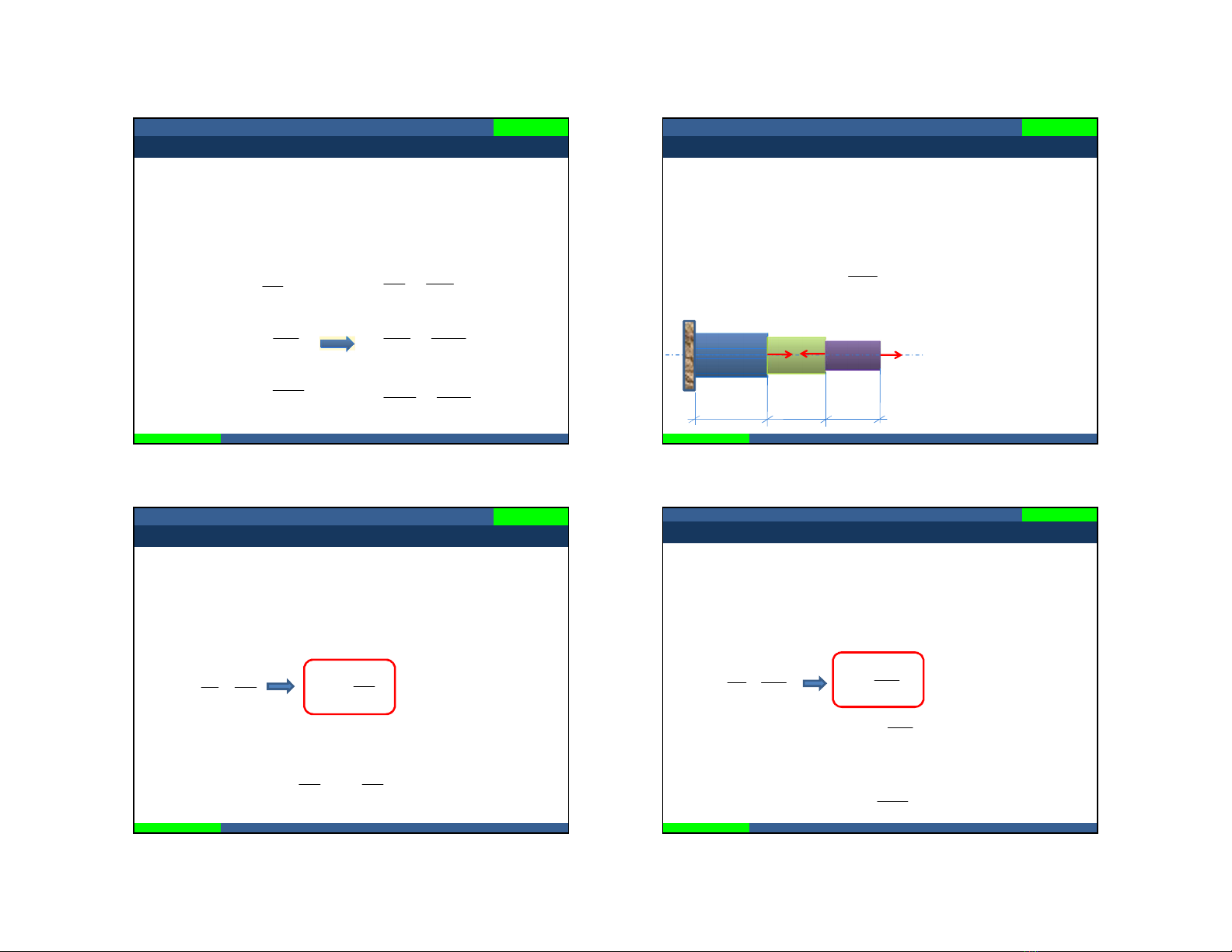
Ví dụ:
Cho E = 2.105N/mm 2
AAB = 20mm2; ABC =
30mm2; ACD = 40mm2
Tính biến dạng dài
tuyệt đối của thanh.
30
cm
20
cm
20
cm
7
kN
5
kN
2
kN
A
B
CD
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.2. Phương pháp tích phân phương trình vi phân
6.2.1. Phương pháp tích phân trực tiếp
6.2.1.3. Thanh chịu xoắn
z
z
M
d
dz GJ
Khi thanh có mặt cắt ngang hình tròn chịu xoắn hay uốn và xoắn
đồng thời, trên mặt cắt ngang có thành phần nội lực Mz. Thành
phần này gây ra biến dạng góc gọi là góc xoắn tương đối giữa
hai cắt ngang của thanh.
0
l
z
z
M
dz
GJ
a. Nếu Mz,G, Jzlà hằng số:
z
z
M
l
GJ
1
n
zi
i
ii zi
M
l
G J
b. Nếu Mz,G, Jzkhông là hằng số, chia thanh ra thành n
đoạn sao cho trên mỗi đoạn 3 đại lượng này đều là hằng số
11/21/2012
3
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.2. Phương pháp tích phân phương trình vi phân
6.2.1. Phương pháp tích phân trực tiếp
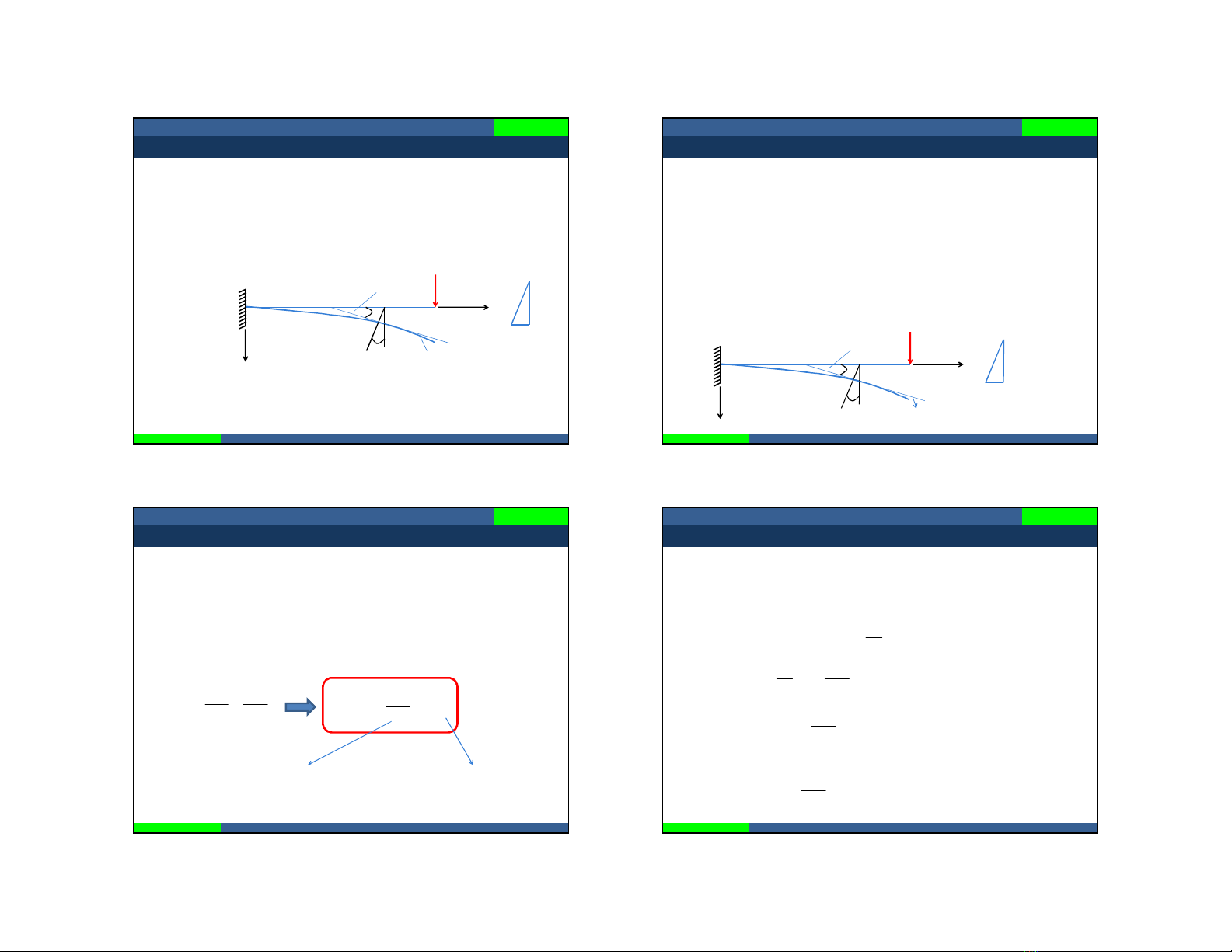
6.2.1.3. Thanh chịu uốn phẳng
-Uốn phẳng: hiện tượng sau khi chịu uốn trục thanh vẫn
nằm trong mặt phẳng tải trọng.
-Đường đàn hồi: trục thanh sau khi biến dạng.
K
K’
P
Đường đàn hồi
z
y
Phương trình của đường đàn hồi y =f(z).
K
K’
v
u
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.2. Phương pháp tích phân phương trình vi phân
6.2.1. Phương pháp tích phân trực tiếp
6.2.1.3. Thanh chịu uốn phẳng
Khi thanh chịu uốn phẳng, trên mặt cắt ngang có thành phần
nội lực MxThành phần này gây ra các biến dạng: độ võng và
góc xoay.
a. Góc xoay
x x
x
d M
dz EJ
1
x
x
x
M
z dz C
EJ
Tích phân bất định Hằng số tích phân
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.2. Phương pháp tích phân phương trình vi phân
6.2.1. Phương pháp tích phân trực tiếp
6.2.1.3. Thanh chịu uốn phẳng
- Để tính độ võng của thanh, ta phân KK’ thành hai thành phần u,
v như hình vẽ. Bài toán được xét trong điều kiện chuyển vị bé nên
có thể xem u << v và có thể bỏ qua thành phần u. Thành phần v
được gọi là độ võng của dầm tại vị trí đang xét.
- Phương trình độ võng của thanh:
v z y z
b. Độ võng
K
K’
P
z
y
K
K’
v
u
Tiếp tuyến với đường đàn hồi tại K’
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.2. Phương pháp tích phân phương trình vi phân
6.2.1. Phương pháp tích phân trực tiếp
- Mối quan hệ giữa độ võng và góc xoay:
6.2.1.3. Thanh chịu uốn phẳng
1 2
x
x
M
y dz C dz C
EJ
- Phương trình vi phân đường đàn hồi:
"
x
x
M
y
EJ
tan
x x
dy
dz
1
x
x
M
dy
dz C
dz EJ
11/21/2012
4
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.2. Phương pháp tích phân phương trình vi phân
6.2.2. Phương pháp hàm đặc biệt
Đọc thêm trong sách lý thuyết trang 203.
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.3. Phương pháp năng lượng
6.3.1. Nguyên lý lực ảo
- Lực ảo: Hệ lực cân bằng tác dụng lên vật mà không gây ra
sự dịch chuyển của các điểm thuộc vật. Lực ảo sinh ra
trường ứng suất ảo. Khi vật biến dạng, điểm đặt các lực ảo bị
dịch chuyển. Công của lực ảo:
*
1 1
n m
e i i i i
i j
W P M
- Công biến dạng ảo trên toàn bộ thể tích (do nội lực gây ra).
* *
V
U d U dV
- Nguyên lý lực ảo: Công ảo ngoại lực thì bằng công biến
dạng ảo.
* *
e
W U
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.3. Phương pháp năng lượng
6.3.2. Biểu thức công biến dạng ảo
a. Công biến dạng ảo gây bởi Nz
*z z
l
N N
U dz
EA
b. Công biến dạng ảo gây bởi Mx
*.
x x
x
l
M M
U dz
EJ
(*)
Công biến dạng phân tố:
.
U
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.3. Phương pháp năng lượng
6.3.3. Phương pháp giải
* Áp dụng phương pháp năng lượng tính độ võng, góc xoay
trong bài toán uốn phẳng.
- Thực nghiệm cho thấy, công biến dạng ảo do lực cắt gây ra
nhỏ hơn nhiều so với phần do moment uốn gây ra. Vì thế,
công biến dạng ảo của thanh sẽ được xác định theo biểu
thức (*).
- Nguyên tắc:
+ Khi tính độ võng, ta sử dụng hệ lực ảo là lực tập
trung có giá trị đơn vị đặt tại vị trí cần tính độ võng.
+ Khi tính góc xoay, ta sử dụng hệ lực ảo là moment
tập trung có giá trị đơn vị đặt tại vị trí cần tính góc xoay.
11/21/2012
5
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.3. Phương pháp năng lượng
6.3.3. Phương pháp giải
a. Độ võng
- Công ngoại lực ảo
*
. 1.
e D D
W P y y
- Công biến dạng ảo:
*.
x x
x
l
M M
U dz
EJ
- Theo nguyên lý lực ảo:
.
x x
D
x
l
M M
y dz
EJ
Độ võng tại một mặt cắt D bất kì
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.3. Phương pháp năng lượng
6.3.3. Phương pháp giải
b. Góc xoay
- Công ngoại lực ảo
*
. 1.
e D D
W M
- Công biến dạng ảo:
*.
x x
x
l
M M
U dz
EJ
- Theo nguyên lý lực ảo:
.
x x
D
x
l
M M
dz
EJ
Góc xoay tại một mặt cắt D bất kì
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.3. Phương pháp năng lượng
6.3.3. Phương pháp giải
- Các tích phân trong các biểu thức (7.20) và (7.23) đươc gọi
là tích phân chập. Để giải các tích phân này, ta sử dụng
phương pháp nhân biểu đồ.
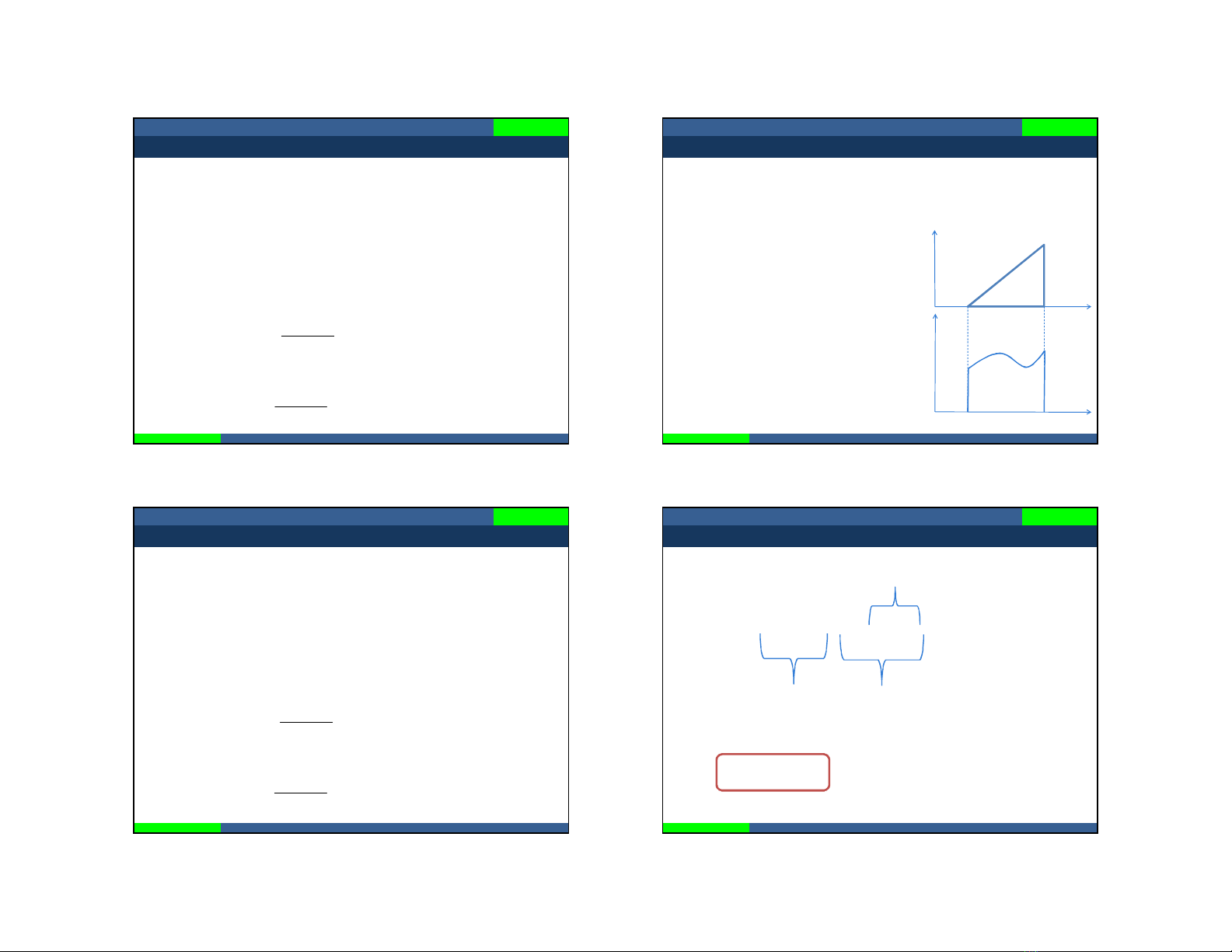
- Xét tích phân chập:
2
1
1 2
z
z
F f z f z dz
2
2
f z
1
f z
1
z
2
z
z
1
f
2
f
1
z
2
z
z
+ Giả sử hàm là hàm tuyến
tính:
1
f z
1 1 2
f z a a z
(7.24)
(7.25)
2
1
1 2 2
z
z
F a a z f z dz
(7.26)
Chương VI: Tính biến dạng thanh
Bộ môn Cơ Kỹ Thuật – Đại học Bách Khoa Tp.HCM
6.3. Phương pháp năng lượng
6.3.3. Phương pháp giải
2 2
1 1
1 2 2 2
z z
z z
F a f z dz a zf z dz
1 2
a
2 2
C
a z
Moment tĩnh đối với f2
2 1 2 2
C
F a a z
2 1 2
C
F f z


























