1
Chương 2
CƠ SỞ VÀ CÁC BƯỚC PHÂN TÍCH CHUNG CỦA FEM
2.2. Trình tự phân tích bài toán theo FEM
2.1. Khái niệm về FEM
2.3. Hàm xấp xỉ – Đa thức xấp xỉ – Phép nội suy biểu diễn
đa thức xấp xỉ theo vectơ các bậc tự do của phần tử {
q
}
e
2.4. Các phương trình cơ bản
Laø moät phöông phaùp soá ñeå tìm daïng gaàn ñuùng cuûa haøm aån trong V. Tuy
nhieân, FEM khoâng tìm daïng xaáp xæ treân toaøn mieàn V maø chæ tìm trong töøng
mieàn con Ve(e: phaàn töû)
Trong FEM, Vñöôïc chia thaønh moät soá höõu haïn caùc Ve– phaàn töû. Caùc
phaàn töû ñöôïc noái keát vôùi nhau taïi caùc ñieåm ñònh tröôùc treân bieân (nuùt).
Trong phaïm vi phaàn töû, ñaïi löôïng caàn tìm ñöôïc xaáp xæ trong daïng haøm ñôn
giaûn, goïi laø caùc haøm xaáp xæ (approximation function).
Caùc haøm naøy ñöôïc noäi suy (bieåu dieãn) qua giaù trò cuûa haøm (ởbài toán liên
tục cấp ), hoặc caû ñaïo haøm (trong bài toán liên tục cấp hoặc ) taïi
caùc ñieåm nuùt treân phaàn töû. Caùc giaù trò naøy ñöôïc goïi laø caùc baäc töï do cuûa
phaàn töû laø aån soá chính cuûa baøi toaùn.
0
C
1
C
2
C
1.1. KHÁI NIỆM
2
Trong cô vaät raén bieán daïng, tuyø theo yù nghóa vaät lyù cuûa haøm xaáp xæ, ta
coù 3 loaïi moâ hình:
1. Moâ hình töông thích: Haøm xaáp xæ bieåu dieãn gaàn ñuùng daïng phaân boá cuûa
chuyeån vò trong phaàn töû. Caùc aån soá laø caùc chuyeån vò hay ñaïo haøm cuûa chuyeån
vò taïi caùc nuùt (vaø có thể ñöôïc xaùc ñònh töø heä phöông trình thieát laäp treân cô sôû
nguyeân lyù theá naêng toaøn phaàn döøng - Nguyeân lyù Lagrange).
2. Moâ hình caân baèng: Haøm xaáp xæ bieåu dieãn gaàn ñuùng daïng phaân boá cuûa öùng
suaát, noäi löïc trong phaàn töû. Caùc aån soá laø löïc taïi caùc nuùt ñöôïc xaùc ñònh töø heä
phöông trình thieát laäp treân cô sôû nguyeân lyù cöïc tieåu cuûa naêng löôïng buø toaøn
phaàn.
3. Moâ hình hoãn hôïp: Haøm xaáp xæ bieåu dieãn gaàn ñuùng daïng phaân boá cuûa caû
chuyeån vò vaø öùng suaát trong phaàn töû. Caùc aån soá ñöôïc xaùc ñònh töø heä phöông
trình thieát laäp treân cô sôû nguyeân lyù bieân phaân Reisner, ….
1.1. KHÁI NIỆM
Böôùc 1: Rôøi raïc hoaù mieàn khaûo saùt: Vñöôïc chia thaønh caùc mieàn con Vecoù
daïng hình hoïc thích hôïp vaø ñôn giaûn.
Böôùc 2: Choïn haøm xaáp xæ thích hôïp : Thöôøng choïn daïng ña thöùc (thöôøng
ñôn giaûn vaø deã thoaû maõn caùc tieâu chuaån hoäi tuï). Roài bieåu dieãn haøm xaáp xæ
theo taäp hôïp giaù trò (caû ñaïo haøm) cuûa noù taïi caùc nuùt cuûa phaàn töû {q}e
Böôùc 3: Thieát laäp ma traän ñoä cöùng phaàn töû [K]evaø vectô taûi phaàn töû {P}e
(moät caùch hình thöùc)
e ee
K q P
2.2. TRÌNH TỰ PHÂN TÍCH BÀI TOÁN THEO FEM
3
Böôùc 4: Gheùp noái caùc phaàn töû treân cô côû moâ hình töông thích vaø keát quaû laø:
K q P
trong ñoù:
laø ma traän cöùng toång theå.
laø vectô taûi toång theå.
vectô chuyeån vò nuùt toång theå
taäp hôïp caùc giaù trò cuûa ñaïi löôïng
caàn tìm taïi taát caû caùc nuùt
K
P
q
Söû duïng ñieàu kieän bieân cuûa baøi toaùn, nhaän ñöôïc heä phöông trình ñeå giaûi:
* * *
K q P
Böôùc 5: Giaûi heä phöông trình ñaïi soá:
* * *
K q P
Böôùc 6: Hoaøn thieän: Tìm noát chuyeån vò, bieán daïng , öùng suaát trong caùc phaàn töû.
2.2. TRÌNH TỰ PHÂN TÍCH BÀI TOÁN THEO FEM
Trong FEM, ñaïi löôïng caàn tìm (chuyeån vò) ñöôïc xaáp xæ hoùa trong
töøng phaàn töû theo 1 haøm xaáp xæ ñôn giaûn daïng ña thöùc:
e
u P a
Ví duï:
Baøi toaùn 1-D:
1 2
2
1 2 3
e
e
u x a a x
u x a a x a x
1
2
2
1 2 1
1
... 1 ...
Ma traän caùc ñôn thöùc
Vectô caùc toïa ñoä toång quaùt
Vectô caùc tham soá cuûa ña thöùc xaáp x
æ
n n
e n
n
P
a
a
a
u x a a x a x x x x
a
2.3. HÀM XẤP XỈ – ĐA THỨC XẤP XỈ – PHÉP NỘI SUY
4
Baøi toaùn 2-D:
2 2
1 2 3 4 5 6
, ,
e
u x y a a x a y a xy a x a y P x y a
2 2
1 2 6
, 1vôùi:
T
P x y x y xy x y
a a a a
Roõ raøng: + Ña thöùc ñöôïc xem nhö toå hôïp tuyeán tính cuûa caùc ñôn thöùc
maø taäp hôïp ñôn thöùc ñoù thoûa maõn yeâu caàu ñoäc laäp tuyeán tính vaø ñaày ñuû.
+ Xaáp xæ daïng ña thöùc deã tính toaùn, deã ñaïo haøm, tích phaân.
Pheùp noäi suy: Caùc heä soá ai cuûa ña thöùc xaáp xæ ñöôïc bieåu dieãn qua
chính caùc giaù trò cuûa noù (hoaëc caû caùc giaù trò ñaïo haøm) taïi caùc ñieåm nuùt
treân phaàn töû ta noùi raèng: Haøm xaáp xæ ñöôïc noäi suy theo giaù trò (ñaïo
haøm) cuûa noù taïi caùc nuùt.
2.3. HÀM XẤP XỈ – ĐA THỨC XẤP XỈ – PHÉP NỘI SUY
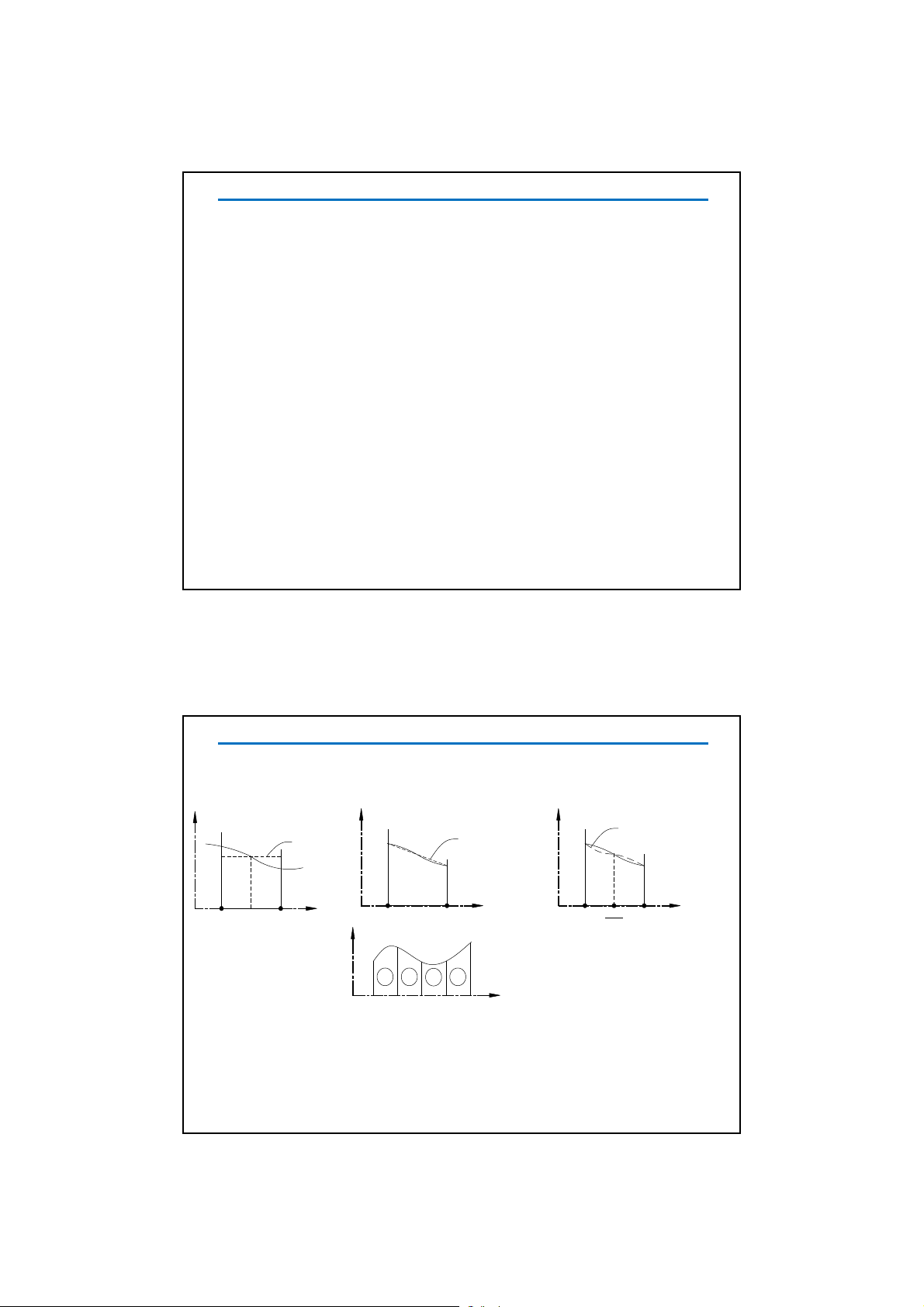
n
3
n1n2n
4
u
x
a b
u (x)=a
01
u
x
a b
u (x)=a +a x
012
n1n2
u
x
a b
u (x)=a +a x+a x
012
n1n3
3
2
n2
a+b
2
u
x
n
5
e
1e
2e
3e
4
Pheùp noäi suy Lagrange
2.3. HÀM XẤP XỈ – ĐA THỨC XẤP XỈ – PHÉP NỘI SUY
5
a. Caùc ña thöùc xaáp xæ phaûi thoûa maõn ñieàu kieän hoäi tuï:
+ Lieân tuïc trong phaàn töû (Ve): Hieån nhieân khi choïn
daïng ña thöùc. + Baûo ñaûm toàn taïi trong Vetraïng thaùi ñôn vò (haèng
soá) vaø caùc ñaïo haøm rieâng cuûa noù ñeán baäc cao nhaát maø phieám haøm
I(u) ñoøi hoûi. + Treân bieân phaàn töû, uvaø caùc ñaïo haøm cuûa noù ñeán
caáp (r–1) laø lieân tuïc.
Trong cô hoïc keát caáu, caùc yeâu caàu treân ñöôïc hieåu nhö laø yeâu
caàu lieân tuïc cuûa bieán daïng, töùc laø: phaàn töû khi bieán daïng khoâng coù
söï ñöùt gaãy beân trong phaàn töû cuõng nhö khi chuyeån töø phaàn töû naøy
sang phaàn töû beân caïnh.
Choïn baäc cuûa ña thöùc xaáp xæ: Caùc yeâu caàu caàn xeùt tôùi:
2.3. HÀM XẤP XỈ – ĐA THỨC XẤP XỈ – PHÉP NỘI SUY
b. Caùc ña thöùc xaáp xæ ñöôïc choïn sao cho khoâng laøm maát tính ñaúng höôùng
hình hoïc Söû duïng tam giaùc Pascal (Baøi toaùn 2-D) hay thaùp Pascal (Baøi
toaùn 3-D).
1
x yxy
x3x y
2xy2y3
x4x y
3x y
2xy3y42
xy
Soá tham soá
3
6
10
3
8
1
xy
zy
x
z
2
2
2
xy
yz
zx
4
10
2.3. HÀM XẤP XỈ – ĐA THỨC XẤP XỈ – PHÉP NỘI SUY