Bạch Vũ Hoàng Lan
1
ĐẠI HỌC KIẾN TRÚC TPHCM
KHOA XÂY DỰNG
Chương 3: HỆ NHIỀU BẬC TỰ DO
𝑝1(𝑡)
𝑝2(𝑡)
𝑚1
𝑚2
𝑐1
𝑐2
𝑘1
𝑘2
3.1 Thiết lập hệ phương trình vi phân chủ đạo
2
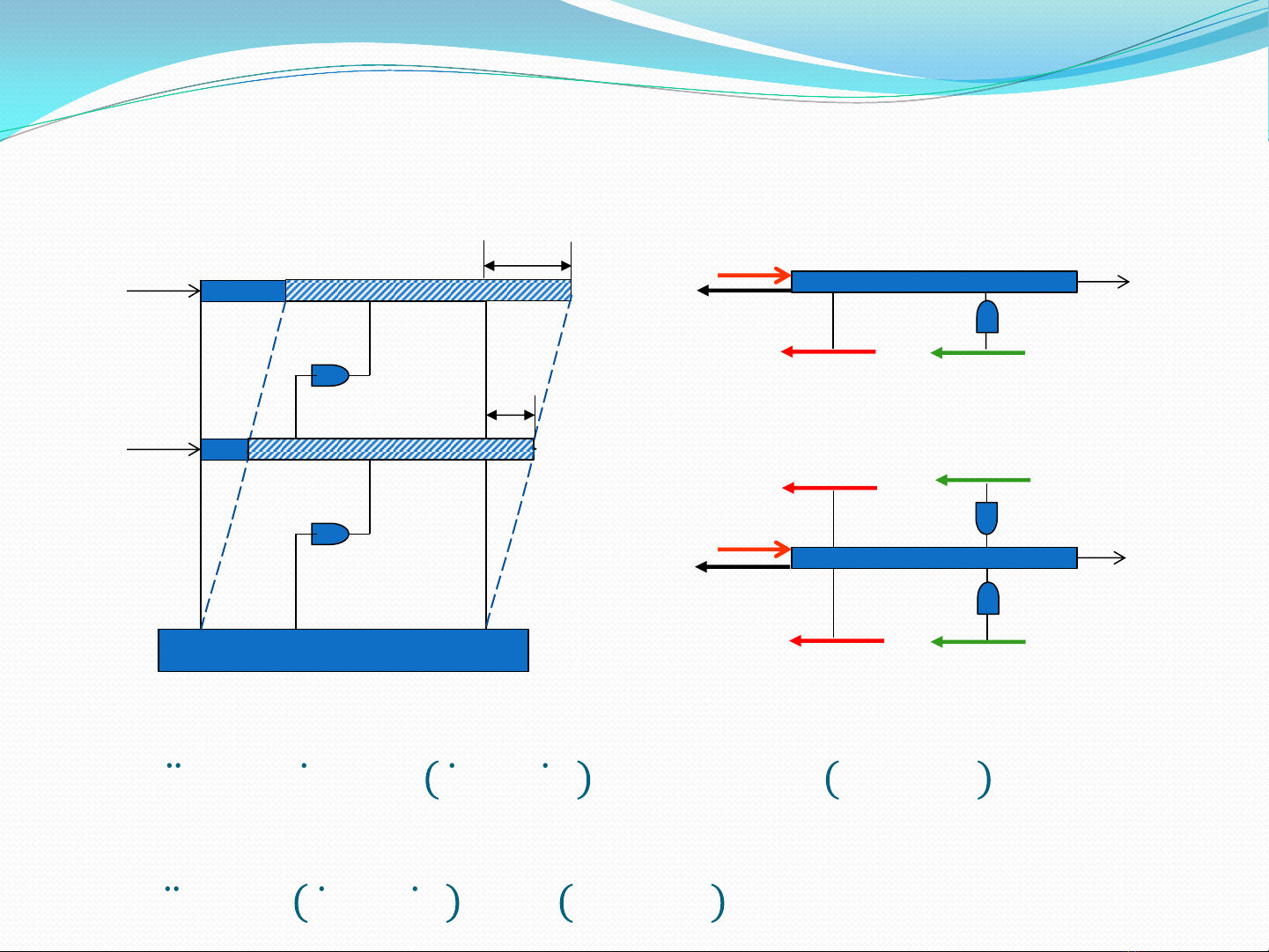
Xét hệ khung phẳng 2 tầng như hình vẽ
Pt cân bằng của khối lượng m1:
𝑚1𝑢
1+𝑐1𝑢
1+𝑐2𝑢
1−𝑢
2+𝑘1𝑢1+𝑘2𝑢1−𝑢2=𝑝1(𝑡)
Khối lượng m2:
𝑚2𝑢
2+𝑐2𝑢
2−𝑢
1+𝑘2𝑢2−𝑢1=𝑝2(𝑡)
𝑝1(𝑡)
𝑝2(𝑡)
𝑢1
𝑢2
𝑚1
𝑚2
𝑐1
𝑐2
𝑘2
𝑐2
𝑘1
𝑘2
𝑓𝐼2
𝑓𝑆1𝐼
𝑓𝐼1
𝑓𝑆1𝑠 𝑓𝐶1𝑠
𝑓𝐶1𝐼
𝑓𝑆2𝑠 𝑓𝐶2𝑠
𝑢1
𝑢2
𝑢2
𝑢1
3.1 Thiết lập hệ phương trình vi phân chủ đạo
3
Viết dưới dạng ma trận:
𝑚10
0 𝑚2𝑢
1
𝑢
2+(𝑐1+𝑐2) −𝑐2
−𝑐2𝑐2𝑢
1
𝑢
2+(𝑘1+𝑘2) −𝑘2
−𝑘2𝑘2𝑢1
𝑢2=𝑝1
𝑝2
𝑚11 𝑚12
𝑚21 𝑚22 𝑢
1
𝑢
2+𝑐11 𝑐12
𝑐21 𝑐22 𝑢
1
𝑢
2+𝑘11 𝑘12
𝑘21 𝑘22 𝑢1
𝑢2=𝑝1
𝑝2
Hoặc:
Tổng quát:
Gọi: 𝑚𝑖𝑗 = lực quán tính tương ứng với 𝑢𝑖 do 𝑢
𝑗=1 gây ra
𝑐𝑖𝑗 = lực cản tương ứng với 𝑢𝑖 do 𝑢
𝑗=1 gây ra
𝑘𝑖𝑗 = lực đàn hồi tương ứng với 𝑢𝑖 do 𝑢𝑗=1 gây ra
3.1 Thiết lập hệ phương trình vi phân chủ đạo
4
Theo phương bậc tự do 𝑢𝑖:
Lực quán tính =
𝑚𝑖𝑗×𝑢
𝑗
𝑛𝑑𝑜𝑓
𝑗=1
Lực cản =
𝑐𝑖𝑗×𝑢
𝑗
𝑛𝑑𝑜𝑓
𝑗=1
Lực đàn hồi =
𝑘𝑖𝑗×𝑢𝑗
𝑛𝑑𝑜𝑓
𝑗=1
Pt cân bằng lực theo nguyên lý D’Alembert:
𝑚𝑖𝑗×𝑢
𝑗
𝑛𝑑𝑜𝑓
𝑗=1 +
𝑐𝑖𝑗×𝑢
𝑗
𝑛𝑑𝑜𝑓
𝑗=1 +
𝑘𝑖𝑗×𝑢𝑗
𝑛𝑑𝑜𝑓
𝑗=1 =pi
Xét tất cả các bậc tự do và viết dưới dạng ma trận:
𝑚𝑖𝑗 𝑢
𝑖+𝑐𝑖𝑗 𝑢
𝑖+𝑘𝑖𝑗 𝑢𝑖= 𝑝𝑖
Với: 𝑑𝑜𝑓 - Degree of Freedom
3.1 Thiết lập hệ phương trình vi phân chủ đạo
5
Hay: 𝐌𝒖
+𝐂𝒖
+𝐊𝒖=𝒑
Trong đó: 𝐌= Ma trận khối lượng
𝐂= Ma trận cản
𝐊= Ma trận độ cứng
Nếu khối lượng của hệ được thu gọn về các bậc tự
do là các chuyển vị thẳng thì 𝑚𝑖𝑗 =0 (𝑘ℎ𝑖 𝑖<>𝑗) và
ma trận khối lượng trở thành ma trận đường chéo
với các khối lượng tương ứng với các bậc tự do là
các chuyển vị thẳng