Chương7: Hàm truyền
7.1. Mạch cộng hưởng
1.Cộng hưởng nối tiếp
2.Cộng hưởng song song
7.2.Định nghĩa hàm truyền
7.3. Tính tuyến tính và bất biến của hệ thống
7.4. Ví dụ về hàm truyền
7.5. Đáp ứng xác lập của tín hiệu điều hòa
7.6. Giản đồ Bode
-Thành phần bậc nhất
-Thành phần bậc hai
CuuDuongThanCong.com https://fb.com/tailieudientucntt
7.1.Mạch cộng hưởng
Mạch cộng hưởng là mạch điện mà trong đó xãy ra hiện
tượng cộng hưởng . Cộng hưởng xãy ra trong mạch tại
tần số mà ở đó tổng điện kháng X(ω) hay tổng điện nạp
B(ω) bằng 0. Như vậy điều kiện cần để xãy ra hiện
tượng cộng hưởng là trong mạch có chứa các phần tử
điện kháng là điện cảm và điện dung.
Ta sẽ xét các trường hợp cộng hưởng:
1.Cộng hưởng nối tiếp
2.Cộng hưởng song song
CuuDuongThanCong.com https://fb.com/tailieudientucntt
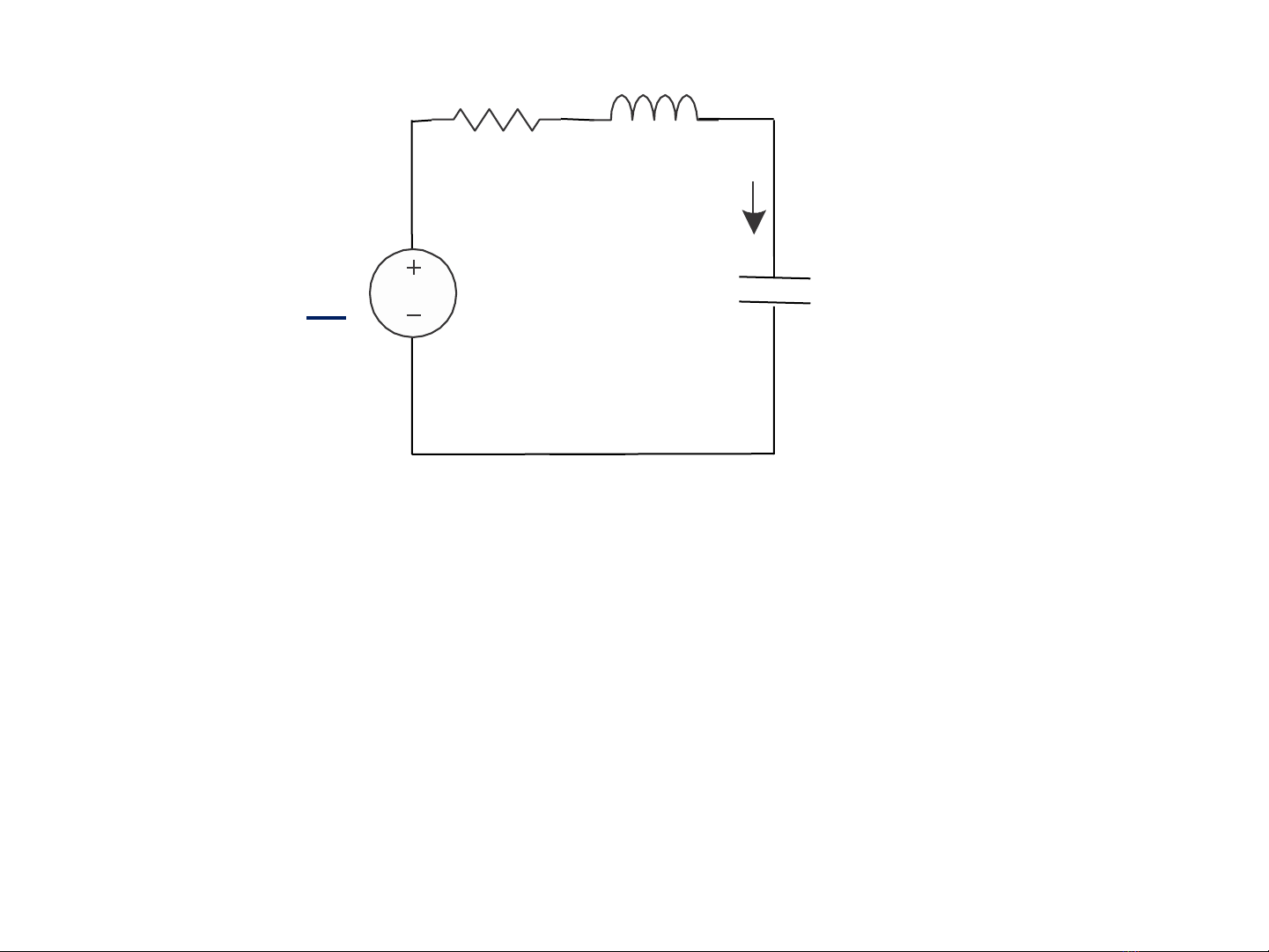
1.Cộng hưởng nối tiếp
*Xét mạch điện như hình. Trong đó: R = R1 + RntL + RntC
R1 : Điện trở mắc vào mạch;
RntL; RntC : Là các điện trở tổn hao trong mô hình nối tiếp của
cuộn dây và tụ điện. Mạch được kích thích bởi nguồn điều hòa
tần số ω. Ta xét mạch ở chế độ xác lập.
Trở kháng của mạch:
Z = R + jωL + 1/jωC = R + j(ωL –1/ωC) = R + jX(ω)
+
-
RjωL
+ -
1/jωCEm /φe
+ -
R
U
L
U
C
U
I
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Mô-đun trở kháng, dẩn nạp của mạch
* Mô-đun trở kháng:
*Góc pha (argument) của trở kháng :
φ(ω) = tg-1 (X/R)= tg-1 [(ωL –1/ωC)/R]
Dẩn nạp của mạch: Y(jω) = 1/Z(jω) = 1/[R + j(ωL –1/ωC)]
*Mô-đun của dẩn nạp:
*Góc pha (argument) của dẩn nạp:
α(ω) = -φ(ω) = -tg-1 (X/R)= -tg-1 [(ωL –1/ωC)/R]
22 )
1
()(
C
LRZ
22 )/1(
1
)(
CLR
Y
CuuDuongThanCong.com https://fb.com/tailieudientucntt
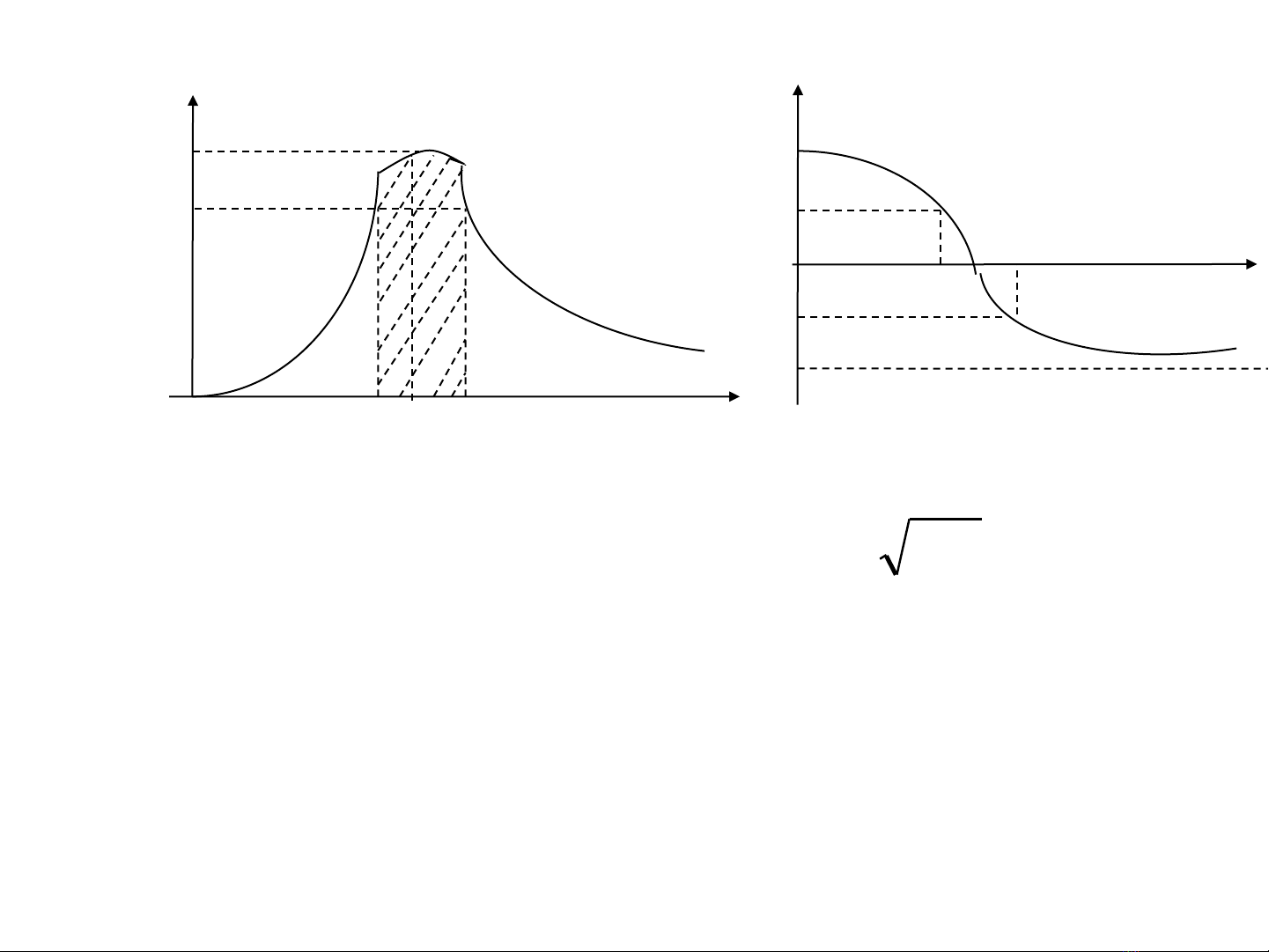
Tính chất lọc thông dải
*Từ đường cong biểu diển như hình ta thấy |Y(ω)| cực đại khi:
ω0 : Tần số cộng hưởng
|Y(ω)| đạt trị giá cực đại là |Y|max =1/R khi đó dòng điện trong
mạch đạt trị giá cực đại có biên độ là Em /R: mạch cộng hưởng
* Với tần số ω cách xa ω0 dòng điện trong mạch giảm dần.
Như vậy nguồn kích thích có tần số ω gần ω0 trong mạch có
dòng điện lớn được xem như đi qua , ngược lại dòng điện bị
chận , ta nói mạch có tính chất lọc thông dải
IY(ω)I
IyImax =1/R
0,707/R
ω0
ωc1 ωc2 ω
ω0ω
ωc1 ωc2
900
-900
450
-450
α(ω)
LC/1
0
CuuDuongThanCong.com https://fb.com/tailieudientucntt