Bài giảng Giải tích mạch - Chương 3: Các phương pháp phân tích mạch

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:124

Thêm vào BST

Báo xấu

8
lượt xem 1
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Chương 3: Các phương pháp phân tích mạch. Sau khi học xong chương này, người học có thể hiểu được một số kiến thức cơ bản về: Phương pháp dòng nhánh; phương pháp điện áp nút - supernodes; phương pháp dòng điện mắt lưới - supermeshes; mạch có ghép hổ cảm; mạch khuếch đại thuật toán (operational amplifier); máy biến áp lý tưởng; nguyên lý tỉ lệ; nguyên lý xếp chồng; biến đổi nguồn; mạch tương đương thévenin và norton; công suất truyền cực đại.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Giải tích mạch - Chương 3: Các phương pháp phân tích mạch

Ch.3:Các phương pháp phân tích mạch. 3.1. Phương pháp dòng nhánh 3.2. Phương pháp điện áp nút. Supernodes. 3.3. Phương pháp dòng điện mắt lưới. Supermeshes 3.4.Mạch có ghép hổ cảm 3.5. Mạch khuếch đại thuật toán (Operational Amplifier) 3.6.Máy biến áp lý tưởng 3.7. Nguyên lý tỉ lệ 3.8. Nguyên lý xếp chồng 3.9. Biến đổi nguồn 3.10. Mạch tương đương Thévenin và Norton 3.11. Công suất truyền cực đại CuuDuongThanCong.com https://fb.com/tailieudientucntt
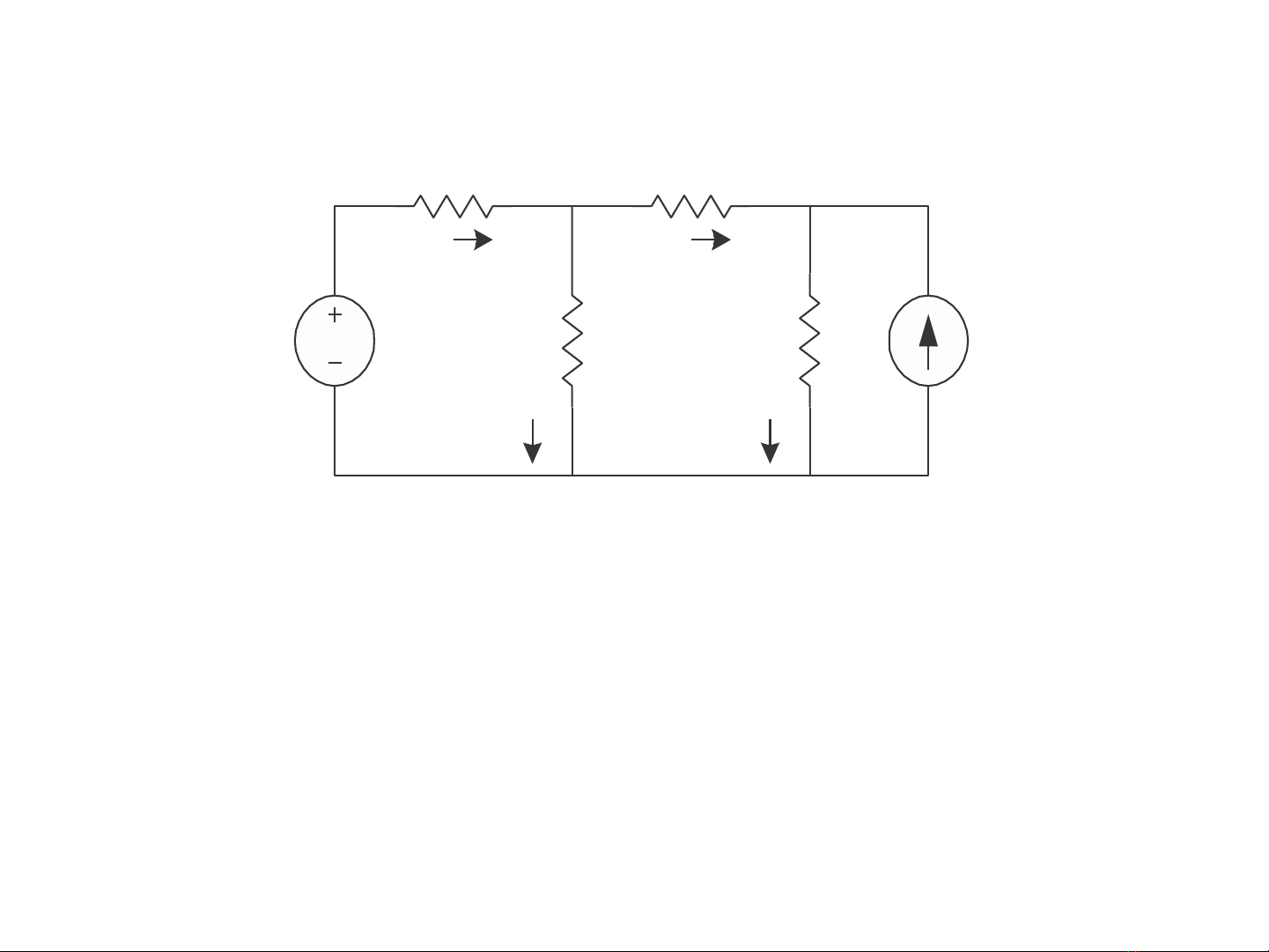
3.1.Phương pháp dòng nhánh 1 kΩ 2 kΩ i1 i3 10V 5 kΩ 10 kΩ 2 mA i2 i4  Tìm n dòng điện nhánh bằng cách viết hệ n phương trình độc lập đối với n dòng nhánh gồm:  (d -1) phương trình viết cho (d - 1) nút dùng KCL  (n-d+1) phương trình viết cho (n – d + 1) vòng hoặc mắt lưới.  Giải hệ n phương trình này ta tìm được dòng điện trong các nhánh . Từ đó suy ra điện áp trên các phần tử…  Ví dụ : Tính i1 ; i2 ; i3 ; i4 của mạch như hình trên? CuuDuongThanCong.com https://fb.com/tailieudientucntt
3.2.Phương pháp điện áp nút Gồm các bước như sau: *Xác định các nút (thiết yếu) của mạch *Chọn 1 nút trong mạch làm nút gốc (có điện áp bằng không), có thể chọn 1 nút tùy ý làm nút gốc nhưng thường ta chọn nút có nhiều nhánh nối tới nhất làm nút gốc (thường là nút ở đáy). Đánh dấu nút gốc bằng ký hiệu nối mass. *Đặt tên cho (d-1) nút còn lại . Điện áp tại 1 nút chính là điện áp của nút đó so với nút gốc. *Áp dụng KCL đối với (d-1) nút trừ nút gốc ta được (d-1) phương trình tuyến tính có (d-1) ẩn số là điện áp tại các nút. *Giải hệ phương trình tuyến tính ta tìm được các điện áp nút. Số phương trình phải giải ít hơn phương pháp dòng nhánh ( d-1 < n) *Suy ra các dòng điện trên các nhánh…. CuuDuongThanCong.com https://fb.com/tailieudientucntt
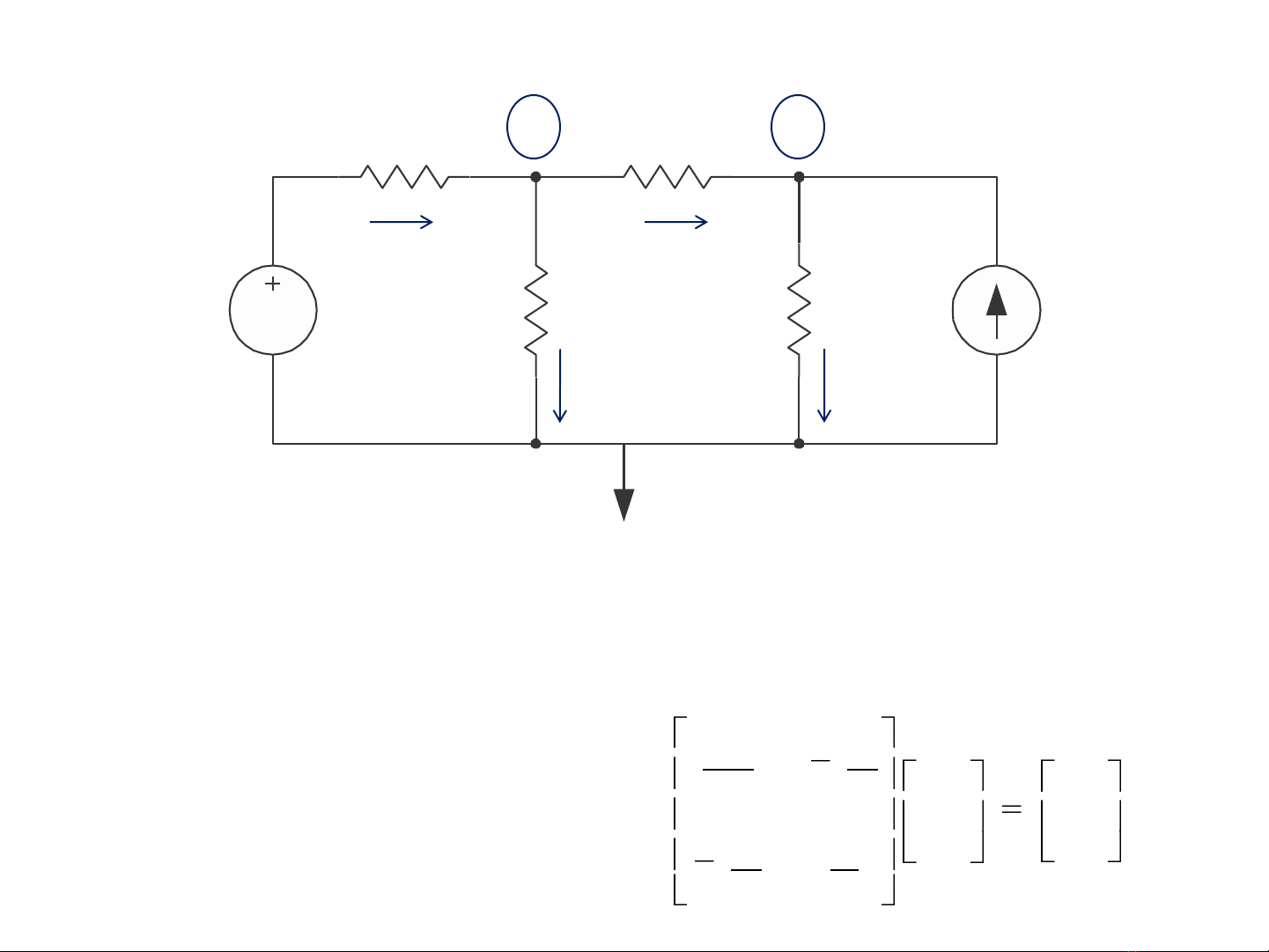
Ví dụ về phương pháp điện áp nút 1 kΩ 1 2 kΩ 2 i1 i3 10V 5 kΩ 10 kΩ 2 mA - i2 i4  Tại nút 1: (10 – V1 )/1 - V1 /5 - (V1 -V2 )/2 = 0. Hay:  17V1 /10 - V2 /2 = 10 . (1)  Tại nút 2: (V1 -V2 )/2 – V2 /10 +2 = 0. Hay:  - V1 /2 +3V2 /5 = 2. (2). Hệ phương trình tuyến tính (1) và (2) viết dưới dạng ma trận: 17 1 V1 10 10 2  Từ (1) và (2)→ V1 = 9,09V; 1 3 V2 2  V2 = 10,95V 2 5 CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ về phương pháp điện áp nút 4Ω 80 Ω + + 144V - V1 10 Ω V2 3A 5Ω - - Tính V1 ; V2 ? CuuDuongThanCong.com https://fb.com/tailieudientucntt
Hệ phương trình trong ph. ph. điện áp nút Vs = RIs R Ta có thể đổi nguồn Vs Is R áp nối tiếp điện trở ra nguồn dòng  Tổng quát hệ phương trình KCL đối với (d-1) nút có dạng sau: Y 11 Y 12 ... Y1 , d 1 1 J1 Y 21 Y 22 ... Y 2 ,d 1 2 J 2 ... ... ... ... . . Yd 1 ,1 Yd 1, 2 ... Yd 1,d 1 d 1 J d 1  Yii (i = 1→ d-1)= Tổng các điện dẩn của các nhánh nối với nút i  Yij = Yji ( i; j = 1→ d-1; i≠j) = - ( Tổng các điện dẩn của các nhánh nối giữa 2 nút i và j.  Ji = Tổng đại số các nguồn dòng tại nút i (mang dấu + nếu đi vào nút và ngược lại sẽ mang dấu -). CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ về phương pháp điện áp nút 4,7 kΩ 2,7 kΩ 2,7 kΩ Tính: v1 ; v2 ; v3 ? + + + 20 mA V1 2 kΩ V2 10 kΩ V3 3,3 kΩ - 5V - - - CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ có nguồn áp phụ thuộc giữa 2 nút 10 Ω VΔ /5 - Tính VΔ ? + 50V 10 Ω 30 Ω 39 Ω VΔ 78 Ω -  Trường hợp mạch có nguồn áp phụ thuộc mắc giữa 2 nút (không kể nút gốc) ta không đổi được nguồn áp ra nguồn dòng tương đương . Để giải mạch ta có 2 cách:  Cách 1:Bằng cách đặt thêm ẩn là dòng chạy qua nguồn áp, sau đó viết hệ phương trình KCL một cách bình thường.  Cách 2 (ít ẩn số hơn): Dùng Supernode để viết phương trình KCL CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ có nguồn áp phụ thuộc giữa 2 nút: đặt thêm ẩn 1 10 Ω 2 VΔ /5 3 - Tính VΔ ? i4 i1 ix i3 + i2 50V 10 Ω 30 Ω 39 Ω VΔ 78 Ω - 0V  Cách 1: Bài toán có 4 ẩn nên ta cần 4 phương trình:  Tại nút 1: V1 = 50. (1).  Tại nút 2: (V1 - V2 )/10 - (V2 /30) + ix = 0. (2)  Tại nút 3: (V3 /39) + (V3 /78) + ix = 0 . (3).  Nguồn áp phụ thuộc: V2 - V3 = VΔ /5 và V3 = VΔ →  V2 - (6V3 /5) = 0 . (4)  Từ (1); (2); (3); (4) → VΔ = V3 = 25,19V CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ có nguồn áp phụ thuộc giữa 2 nút dùng supernode 1 10 Ω 2 VΔ /5 3 supernode - Tính VΔ ? i4 i1 i3 + i2 50V 10 Ω 30 Ω 39 Ω VΔ 78 Ω - 0V  Cách 2: Bài toán có 3 ẩn nên ta cần 3 phương trình:  Tại nút 1: V1 = 50. (1).  Nguồn áp phụ thuộc: V2 - V3 = VΔ /5 và V3 = VΔ →  V2 - (6V3 /5) = 0 . (2)  Tại supernode:  (V1 - V2 )/10 - (V2 /30) - (V3 /39) - (V3 /78) = 0 . (3)  Từ (1); (2); (3) → VΔ = V3 = 25,19V CuuDuongThanCong.com https://fb.com/tailieudientucntt
V.D. có nguồn áp phụ thuộc giữa 2 nút dùng supernode 35 iφ 2Ω 1Ω 4Ω + vΔ - 3,125vΔ 20 Ω 20V 40 Ω 80 Ω iφ  (P.4.29.)  Tính công suất phát ra bởi nguồn 20V?  Trả lời: 602,5 W CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ về phương pháp điện áp nút 500 Ω 11 mA 25 kΩ i1 20V 1 kΩ 10V i2 250 Ω i3  (P.4.24).  Tính i1 ; i2 ; i3 ?  Trả lời: 1mA; -20mA; 31mA CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ về phương pháp điện áp nút 1Ω 1A 2Ω i + 4Ω 3i V 2Ω 1Ω -  Tính V? CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ về dùng ph.ph. điện áp nút 1Ω j2 Ω 5Ω I x I b 10,6/00 I a I c -j5 Ω A 10 Ω 20 I x  Dùng phương pháp điện áp nút tính các dòng nhánh I a ; I ; I ? b c CuuDuongThanCong.com https://fb.com/tailieudientucntt
1 1Ω j2 Ω 2 5Ω 10,6/00 + I x + 10 Ω V2 -j5 Ω A V1 20 I x - -  Ta có: -10,6 + ( V1 /10) + (V1 - V2 ) /(1 + j2) = 0 (1)  ( V2 - V1 )/(1 + j2) + V2 /(-j5) + ( V2 - 20 I x )/5 = 0 (2)  I x = ( V1 - V2 )/(1 + j2) ; Thế I x vào (2) ta có:  - 5V + (4,8 + j0,6) V = 0 (3) 1 2  Từ (1) và (3) ta có: V = 68,40 – j16,80 V; V2 = 68 – j26 V . 1  → I a = V1 /10 = 6,84 – j1,68 A   I x = ( V1 - V2 )/(1 + j2) = 3,76 + j1,68 A  I = ( V - 20 I x )/5 = -1,44 – j11,92 A b 2  I c = V2 /(-j5) = 5,2 + j13,6 A CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ về dùng ph.ph. điện áp nút (A.P.9.12) + 20 Ω is 5Ω 9 µF vs v(t) 100 µH -  Dùng phương pháp điện áp nút tìm v(t)? Biết  is = 10cosωt A; vs = 100sinωt V với ω = 50krad/s  Trả lời: v(t) = 31,62cos(50000t – 71,570 ) V CuuDuongThanCong.com https://fb.com/tailieudientucntt
(P.9.54).Ví dụ về dùng ph.ph. điện áp nút j3 Ω -j3 Ω 5Ω + V - 0 5/00 5/-900 j2 Ω A V Dùng phương pháp điện áp nút tìm V0 (ảnh phức của điện áp v0 )? Trả lời: 9 – j15 = 17,49/-59,040 V CuuDuongThanCong.com https://fb.com/tailieudientucntt
(P.9.56).Ví dụ về dùng ph.ph. điện áp nút j5 Ω + -j10 Ω V0 8Ω 15 0 0 A - I1 2,5I1 Dùng phương pháp điện áp nút tìm V0 ? Trả lời: 72 + j96 = 120/53,130 V CuuDuongThanCong.com https://fb.com/tailieudientucntt
3.3.Phương pháp dòng điện mắt lưới Chỉ áp dụng cho mạch điện phẳng, gồm các bước sau: *Đặt tên cho các mắt lưới. Mỗi mắt lưới ta gán cho nó 1 biến (không có ý nghĩa vật lý) gọi là dòng điện mắt lưới chạy dọc theo các nhánh của mắt lưới. Chiều các dòng điện mắt lưới có thể chọn tùy ý, nhưng thường ta chọn nó cùng chiều với nhau. *Áp dụng KVL cho mỗi mắt lưới, dòng điện mỗi nhánh được biểu diễn bằng tổng đại số các dòng mắt lưới chạy qua nhánh đó. Có (n- d+1) ẩn số (dòng điện mắc lưới) nên cần áp dụng cho (n- d+1) mắc lưới. *Giải hệ phương trình tuyến tính tìm ra các dòng điện mắt lưới. *Suy ra các dòng điện nhánh v.v…. CuuDuongThanCong.com https://fb.com/tailieudientucntt
Hệ phương trình trong ph. ph. dòng điện mắt lưới Đối với mạch có n nhánh , d nút , số mắt lưới L = n – d +1 người ta chứng minh được rằng hệ phương trình đối với (n – d +1) dòng điện mắt lưới được viết dưới dạng ma trận: Z 11 Z 12 ... Z 1L im 1 E m1 Z 21 Z 22 ... Z 2 L im 2 E m 2 ... ... ... ... . . Z L1 Z L 2 ... Z LL i mL E mL Zii = Tổng các điện trở của các nhánh thuộc mắt lưới i (i:1 →L) Zij = Zji (i,j:1 →L; i≠j) = Tổng các điện trở của các nhánh chung giữa 2 mắt lưới i và j, có dấu + nếu trên nhánh chung 2 dòng mắt lưới cùng chiều và ngược lại thì có dấu -. Nếu các dòng mắt lưới chọn cùng chiều thì hệ quả Zij luôn có dấu - Emi = Tổng đại số các sức điện động thuộc mắt lưới i, có dấu + nếu dòng mắt lưới i đi từ cực – đến cực + của nguồn sức điện động và ngược lại có dấu - CuuDuongThanCong.com https://fb.com/tailieudientucntt