Chương 2: Mạch xác lập điều hòa
2.1.Phân tích mạch tuyến tính ở trạng thái xác
lập.
2.2.Phương pháp ảnh phức
2.3.Quan hệ dòng áp trên các phần tử R,L,C .
Định luật Ohm dạng phức
2.4.Trở kháng và dẩn nạp
2.5.Định luật Kirchhoff dạng phức
2.6.Đồ thị véc tơ
2.7.Công suất xoay chiều (AC).
2.8.Phối hợp trở kháng giữa tải và nguồn
CuuDuongThanCong.com https://fb.com/tailieudientucntt
2.1.Phân tích mạch tuyến tính ở trạng thái xác lập
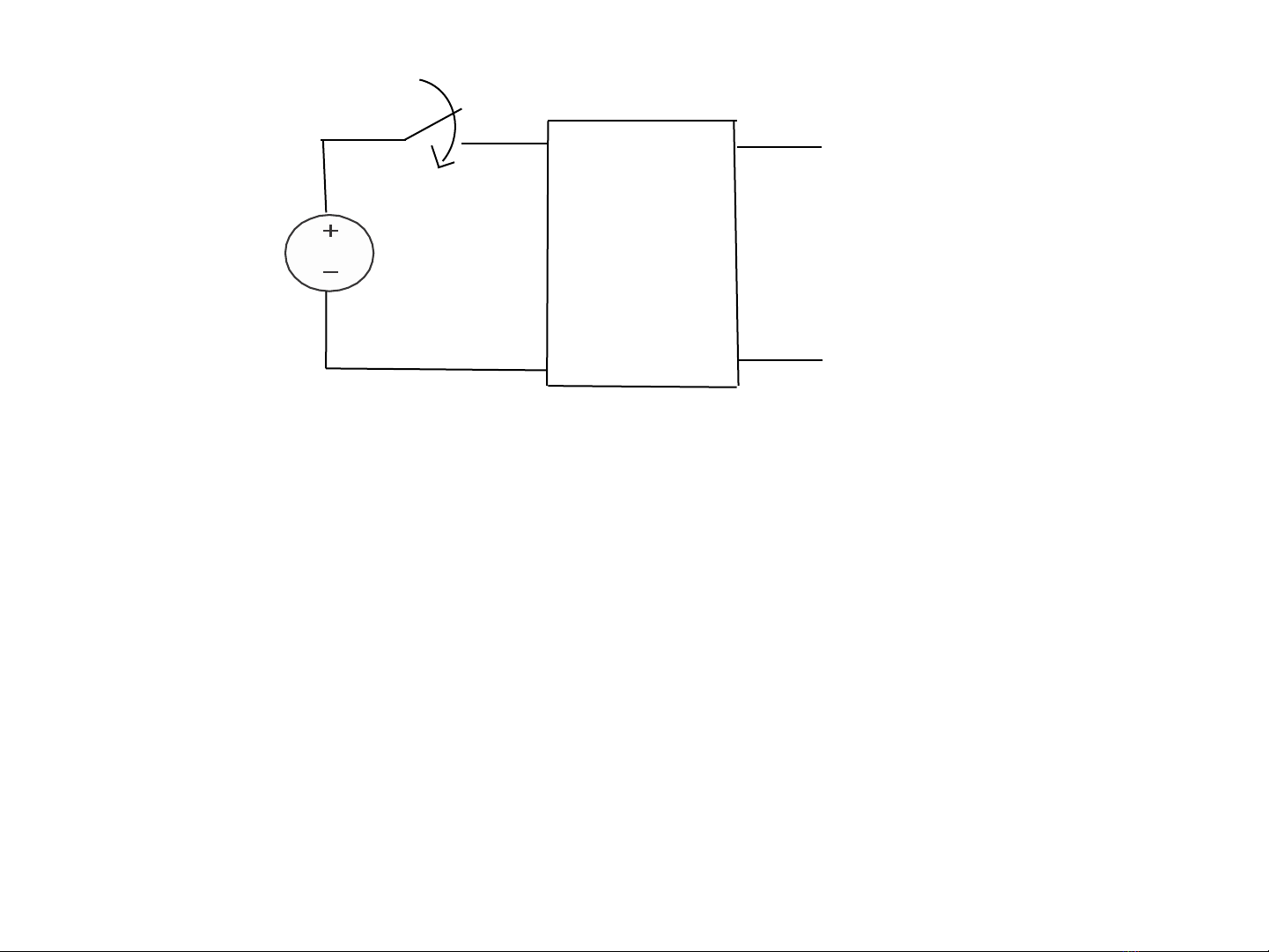
Xét mạch như hình. Tại t = 0 khóa đóng, đáp ứng ngõ ra v0
gồm 2 thành phần:
*Thành phần xác lập vẫn được duy trì khi t → ∞
*Thành phần quá độ tiến tới 0 khi t → ∞
Trong chương này ta xét các phương pháp phân tích mạch
tuyến tính, thông số tập trung ở trạng thái xác lập. Các kích
thích là các nguồn áp, nguồn dòng biến thiên hình sin theo thời
gian với cùng tần số góc ω. Các đáp ứng là dòng điện, điện áp
trên các nhánh, các phần tử cũng có dạng sin với cùng ω.
Asin(ωt)
t = 0 Mạch
tuyến
tính
+
v0
-
CuuDuongThanCong.com https://fb.com/tailieudientucntt
2.2.phương pháp ảnh phức
*Đối với mạch kích thích điều hòa, các dòng điện, các
điện áp trên các nhánh, trên các phần tử đều biến thiên
hình sin cùng tần số ω với nguồn kích thích và chúng
chỉ khác nhau về biên độ và góc pha ban đầu.
*Khi phân tích mạch tuyến tính xác lập điều hòa, có thể
tránh việc giải hệ phương trình vi phân bằng cách dùng
phương pháp ảnh phức. Theo phương pháp này, mỗi
đại lượng điều hòa sẽ được biểu diễn bằng một số phức
(gọi là ảnh phức của nó) có mô-đun bằng biên độ và
argumen bằng góc pha ban đầu của đại lượng điều hòa,
như vậy việc giải hệ phương trình vi phân sẽ được qui
về giải hệ phương trình đại số tuyến tính đối với các ảnh
phức của các biến tức thời
AtA )cos(
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ôn lại số phức
*Dạng đại số:z = x + jy;
x là phần thực của z: x = Re{z}; y là phần ảo của z: y = Im{z}
*Dạng tọa độ cực:
Công thức Euler: e±jФ= cosФ±jsinФ
Re{e±jФ} = cosФ; Im{e±jФ} = sinФ
*Số phức liên hợp
1j
j
rerz
),(;
22 yxangleyxr
j
rezrzjyxz
***
jjjj eeee
2
1
coscos2
jjjj ee
j
jee
2
1
sinsin2
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Mặt phẳng phức
Trục o (y)
Trục thực (x)
y
z
x
r
Ф
j
rezrzjyxz
Tìm biểu thức tương đương của:
CuuDuongThanCong.com https://fb.com/tailieudientucntt