
Bài toán tìm kiếm II
THS. BÙI THỊ DANH
BM.KHMT, KHOA CNTT, ĐH.KHTN TP.HCM
CÁC HỆ THỐNG THÔNG MINH NHÂN TẠO & ỨNG DỤNG
Nội dung
Heuristic
Tìm kiếm tham lam
Thuật giải A*
Sự nới lỏng
2
Heuristic
Các thuật toán tìm kiếm mù duyệt trạng thái theo mọi hướng, không sử dụng thông tin của
trạng thái đích.
3
Ước lượng chi phí
đến trạng thái đích.
Liệu có tìm đường
nhanh hơn?!?
Heuristic
Heuristic là một hàm ước lượng mức độ gần của một trạng thái so với trạng thái đích
◦Kí hiệu là h(s), với s là trạng thái.
Heuristic được thiết kế cho từng bài toán tìm kiếm cụ thể
Một số hàm heuristic phổ biến:
◦Khoảng cách Euclidean, Mahattan.
◦…
4
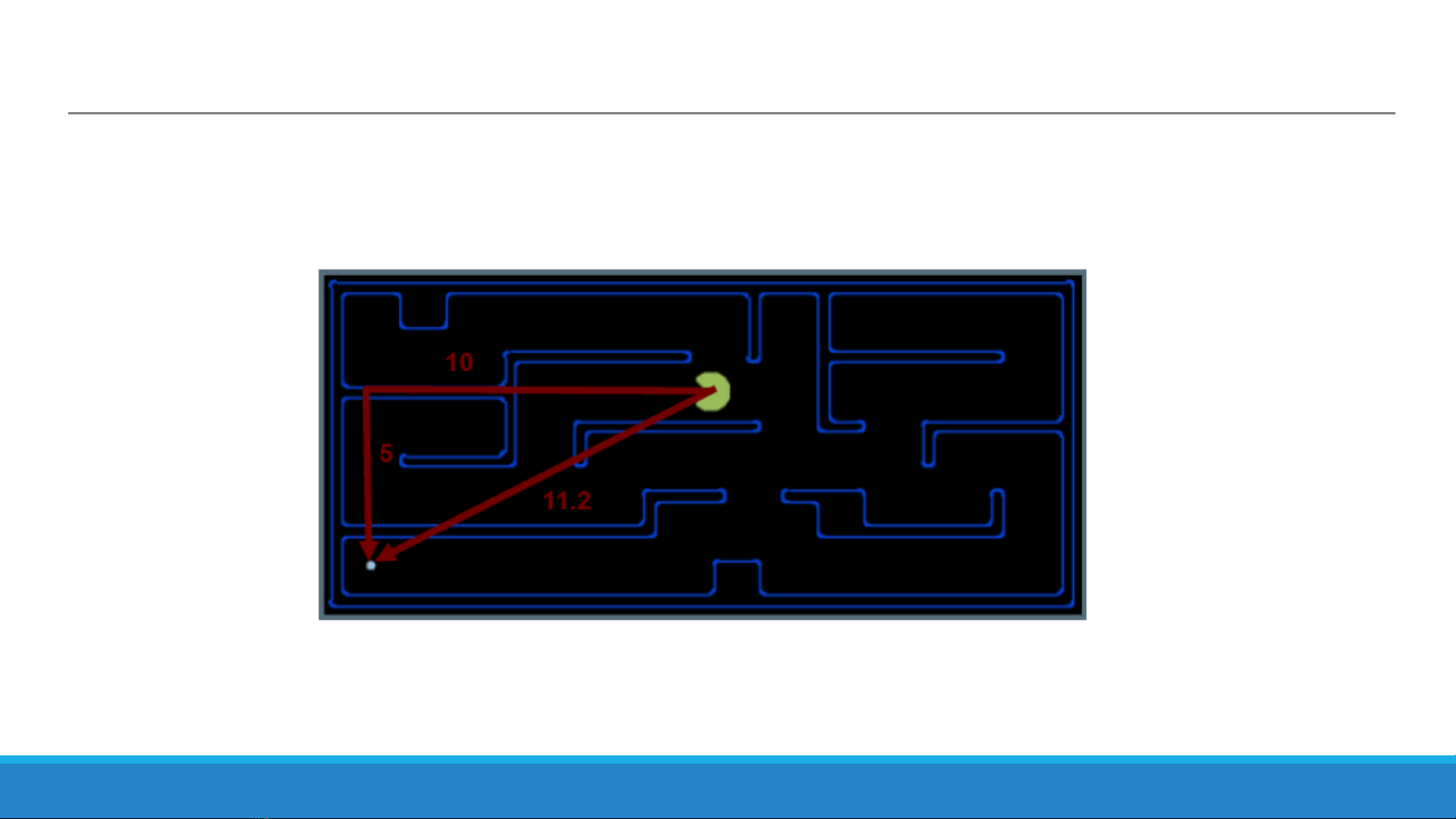
Ví dụ - Tìm đường đi cho Pacman
Hàm h(s) là hàm Euclidean
5


























