
Logic
THS. BÙI THỊ DANH
BM.KHMT, KHOA CNTT, ĐH.KHTN TP.HCM
CÁC HỆ THỐNG THÔNG MINH NHÂN TẠO & ỨNG DỤNG
Nội dung chính
Tổng quan
Logic mệnh đề
Logic bậc nhất
2
Lịch sử phát triển
Thế kỉ 4 TCN, Aristotle phát minh logic tam đoạn luận, hệ thống suy diễn
hình thức đầu tiên.
1879, logic mệnh đề hiện đại được phát triển bởi Gottlob Frege
Logic là mô hình chủ đạo trong lĩnh vực trí tuệ nhân tạo trước những năm
1990s
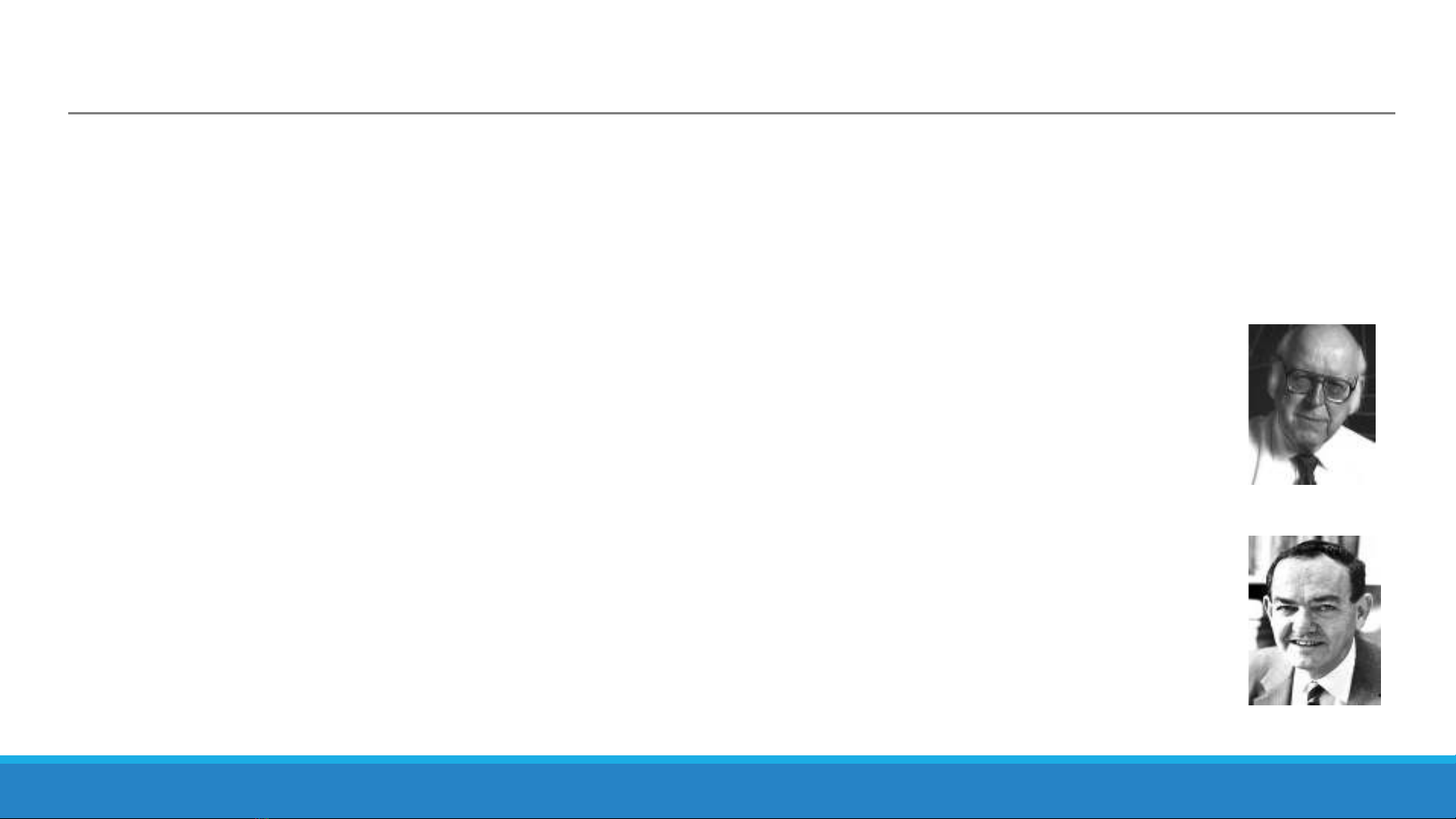
◦1956, Allen Newell và Herbert Simon demo “Logic Theorist”, chương trình AI sử dụng
heuristic chứng minh 38 định lí trong số 52 định lý trong cuốn “Principa Mathematica”
của Whitehead và Russell.
◦1965, J. Alan Robinson phát minh ra phương pháp chứng minh hợp giải.
◦1972, Alain Colmerauer phát triển ngôn ngữ Prolog
3
Allen Newell
Herbert Simon
Lịch sử phát triển
Ngày nay, logic không còn là mô hình ưa thích do sự phát triển của xác suất và máy học
Các nguyên nhân:
◦Xác định, không xử lý trường hợp không chắc chắn; trong khi mô hình xác suất thì có
◦Là mô hình dựa trên luật cứng nhắc; trong khi máy học có thể tự động điều chỉnh mô hình dựa vào dữ
liệu.
Ưu điểm của logic là cung cấp sự diễn đạt ý nghĩa và súc tích
4
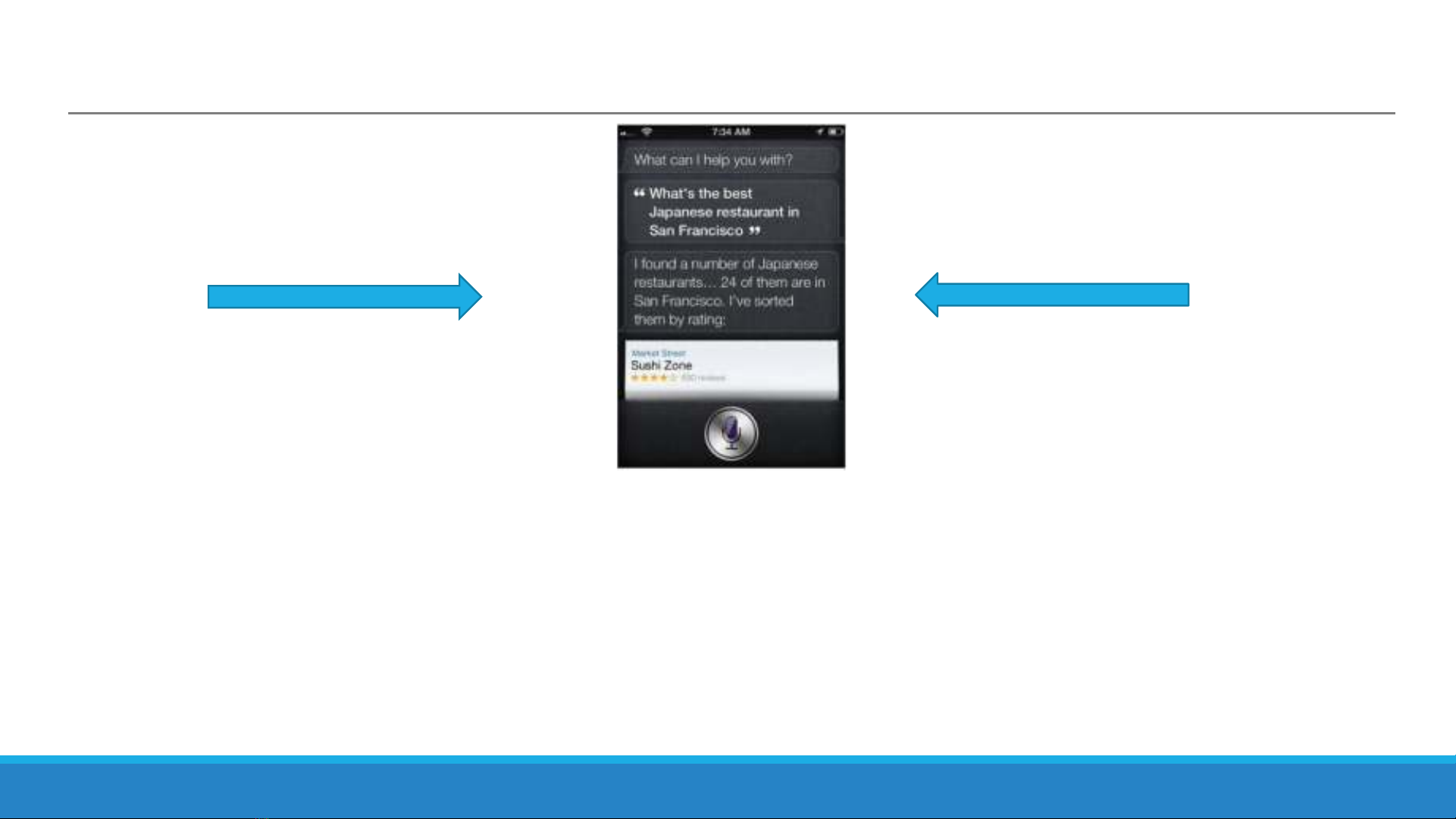
Ứng dụng: trợ lí ảo
Sắp xếp các thông tin không đồng nhất
Lập luận với các thông tin có được
5
Đưa thông tin Đặt câu hỏi
Sử dụng ngôn ngữ tự nhiên


























