3
18/02/2011
1.1 Định nghĩa đồ thị
Lý thuyết đồ thị
Định nghĩa 2.
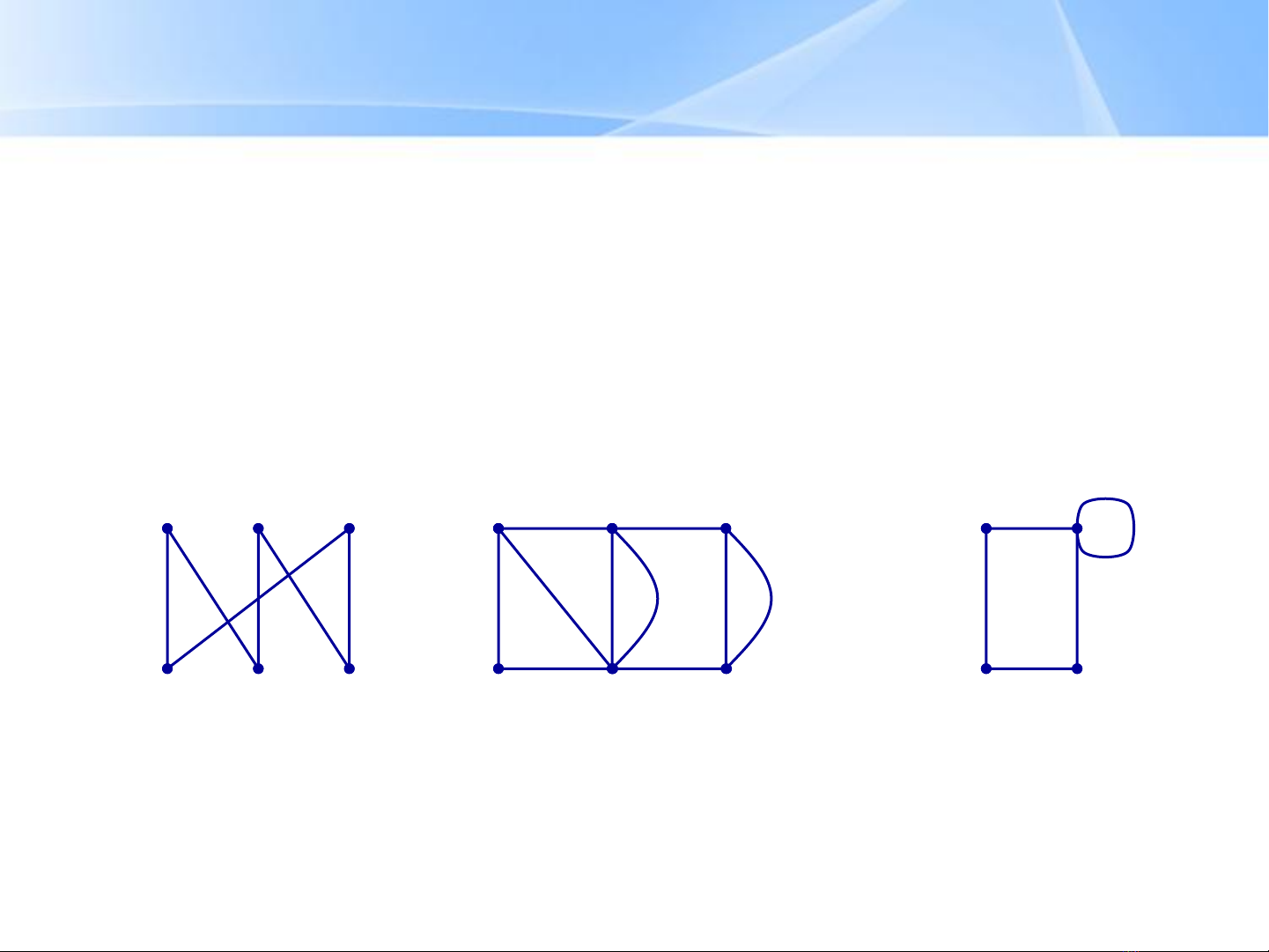
Đa đồ thị vô hướng G = (V,E) bao gồm Vlà tập các
đỉnh,và Elà họ các cặp không có thứ tự gồm hai phần tử
khác nhau của Vgọi là các cạnh. Hai cạnh e1và e2được
gọi là cạnh song song nếu chúng cùng tương ứng một cặp
đỉnh.
Ví dụ
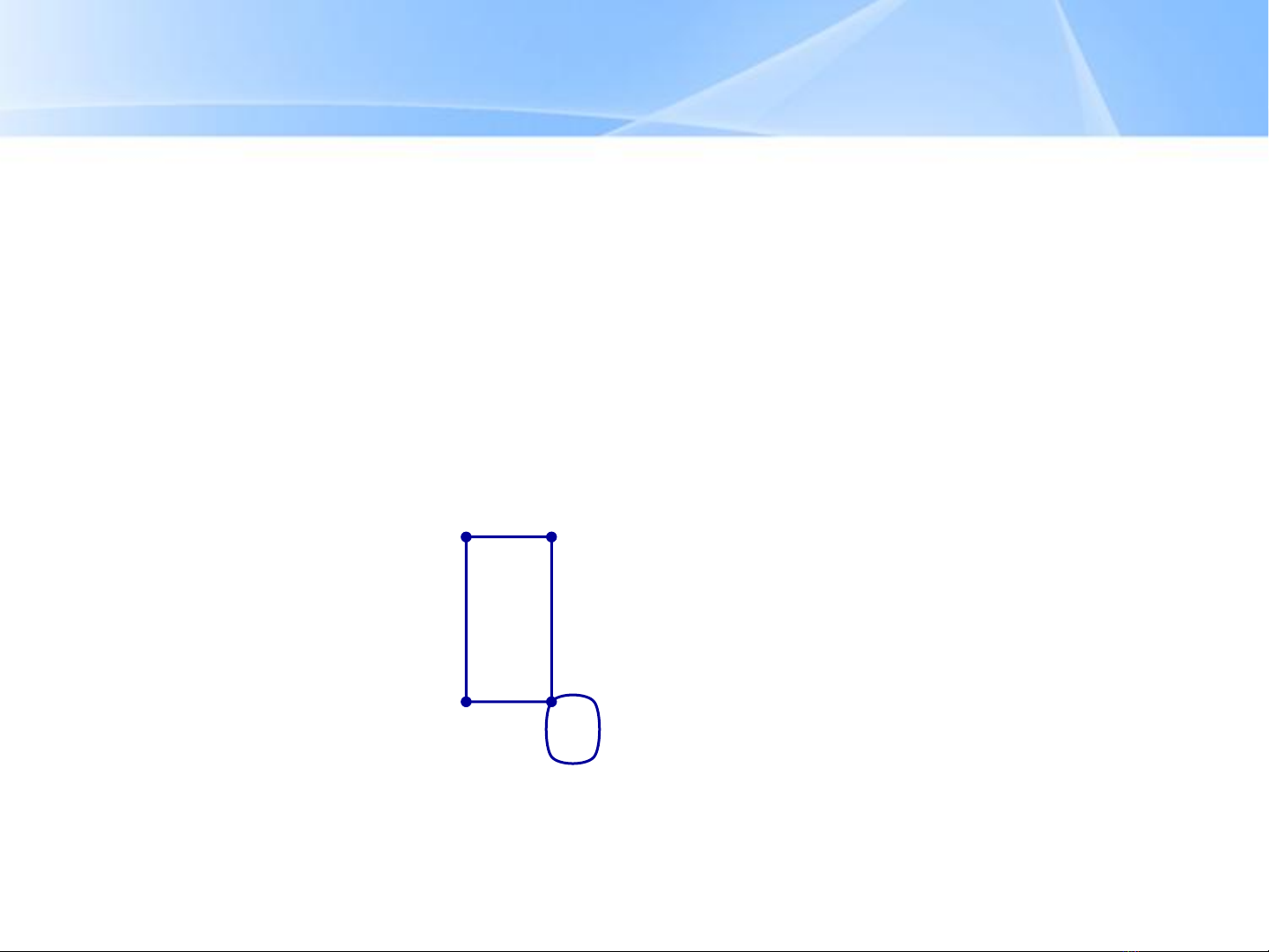
Đa đồ thị vô hướng. e1và e2là
các cạnh song song.
e1
e2