Trang 286
Lý thuyết Ôtômát & NNHT - Khoa Công NghệThông Tin
Chương 9 Máy Turing
PDA vềmột mặt nào đómạnh hơn rất nhiều FSA.
NNPNC-PDA vẫn còn giới hạn. Bên ngoài nó là gì?
FSA và PDA khác nhau ởbản chất của bộ lưu trữtạm thời.
Nếu PDA dùng hai, ba stack, một hàng (queue), hay một thiết
bị lưu trữkhác nào đó thì sức mạnh sẽthếnào?
Mỗi thiết bị lưu trữ định nghĩa một loại ôtômát mới và thông
qua nó một họngôn ngữmới?
Ôtômát có thể được mởrộng đến chừng nào? Khả năng mạnh
nhất có thểcủa ôtômát? Những giới hạn của việc tính toán?
Máy Turing ra đời và khái niệm vềsựtính toán có tính máy
móc hay giải thuật (mechanical or algorithmic computation).
Máy Turing là khá thô sơ, nhưng đủ sức để bao trùm các quá
trình rất phức tạp và luận đề Turing (Turing thesis) cho rằng
bất kỳquá trình tính toán nào thực hiện được bằng các máy tính
ngày nay, đều có thểthực hiện được bằng máy Turing.
Trang 287
Lý thuyết Ôtômát & NNHT - Khoa Công NghệThông Tin
Chương 9 Máy Turing
9.1 Máy Turing chuẩn
9.2 Kết hợp các máy Turing cho các công việc phức tạp
9.3 Luận đề Turing
Trang 288
Lý thuyết Ôtômát & NNHT - Khoa Công NghệThông Tin
Máy Turing chuẩn
Định nghĩa 9.1
Một máy Turing M được định nghĩa bằng bộbảy
M= (Q, Σ, Γ, δ, q0, , F),
−Q là tập hữu hạn các trạng thái nội,
−Σlà tập hữu hạn các kí hiệu được gọi là bảng chữcái ngõ nhập,
−Γlà tập hữu hạn các kí hiệu được gọi là bảng chữcái băng,
−δlà hàm chuyển trạng thái,
−∈Γlà một kí hiệu đặc biệt,
gọi là khoảng trắng (blank),
−q0∈Qlà trạng thái khởi đầu,
−F⊆Qlà tập các trạng thái kết thúc.
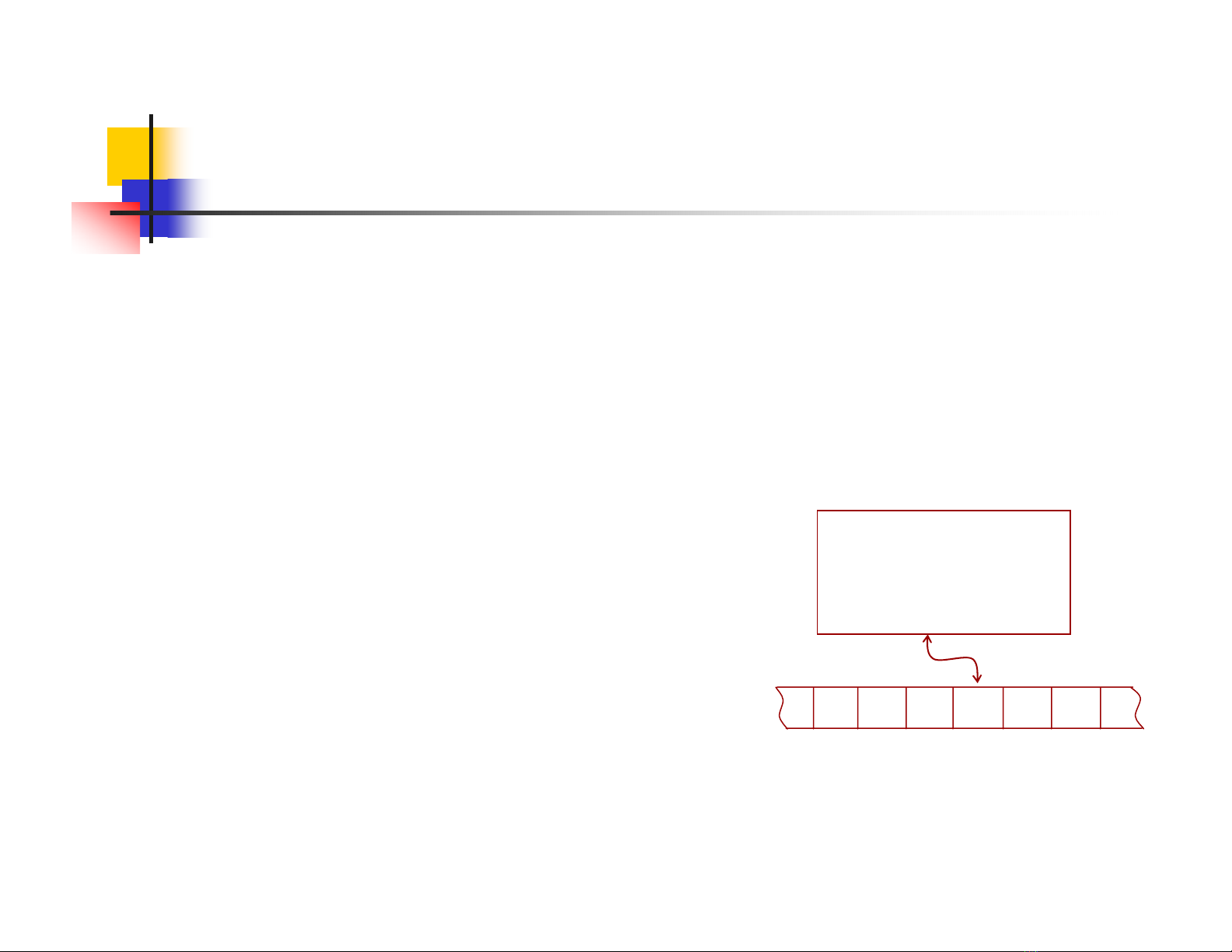
Control unit
Input, Storage,
Output
Trang 289
Lý thuyết Ôtômát & NNHT - Khoa Công NghệThông Tin
Máy Turing chuẩn (tt)
Trong định nghĩa chúng ta giảthiết rằng Σ⊆Γ-{}.
Hàm δ được định nghĩa như sau
δ: Q×Γ→Q×Γ×{L, R}
Nó được diễn dịch như sau: Các đối sốcủa δlà trạng thái hiện
hành của ôtômát và kí hiệu băng đang được đọc. Kết quảlà một
trạng thái mới của automat, một kí hiệu băng mới thay thếcho
kí hiệu đang được đọc trên băng và một sựdi chuyển đầu đọc
sang phải hoặc sang trái.
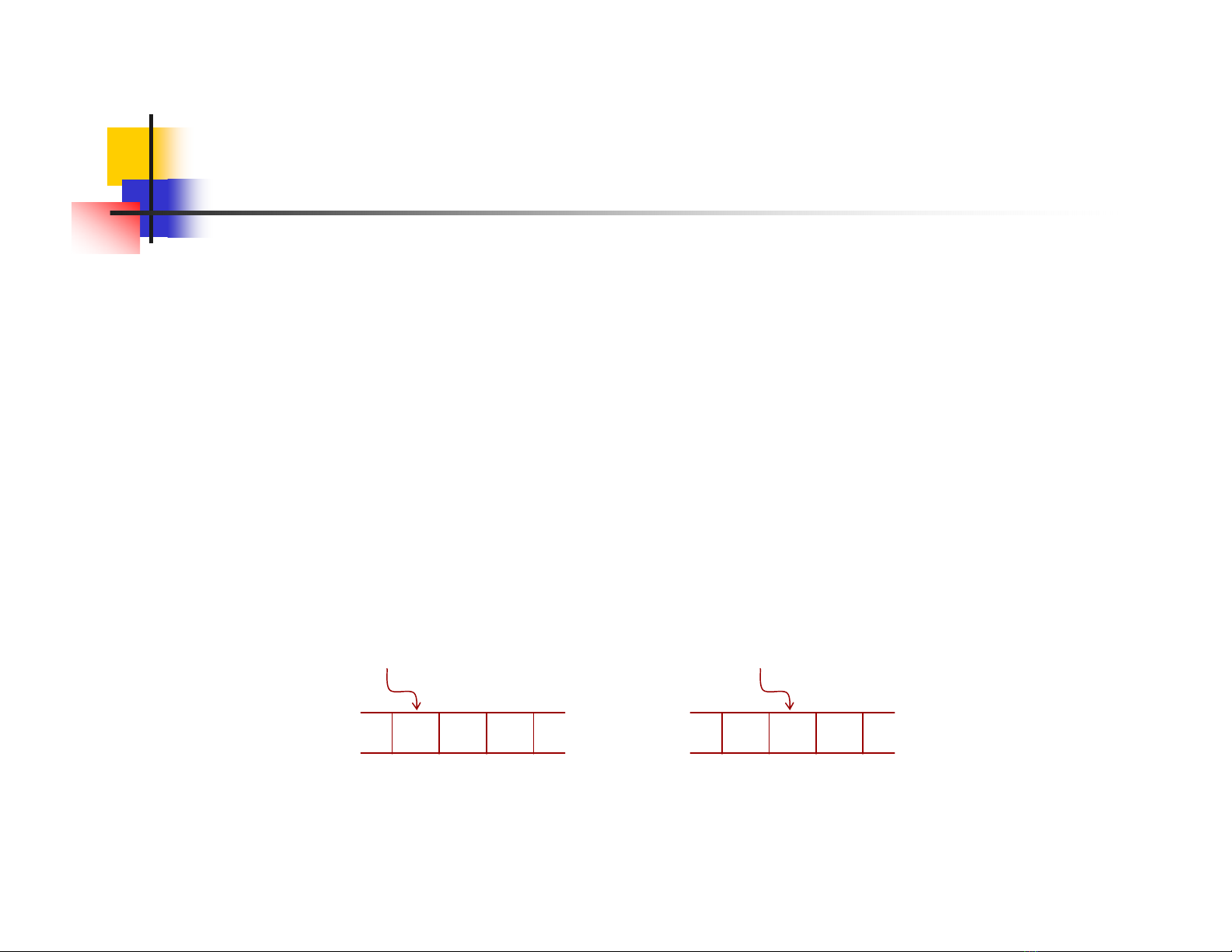
Ví dụδ(q0, a) = {q1, d, R}
abc dbc
Trạng thái nộiq0Trạng thái nộiq1
Trang 290
Lý thuyết Ôtômát & NNHT - Khoa Công NghệThông Tin
Ví dụ
Xét một máy Turing được định nghĩa như sau
Q= {q0, q1}, Σ= {a, b}, Γ= {a, b, }, F= ∅, còn δ được định
nghĩa
δ(q0, a) = (q1, a, R)δ(q1, a) = (q0, a, L)
δ(q0, b) = (q1, b, R)δ(q1, b) = (q0, b, L)
δ(q0, ) = (q1, , R)δ(q1, ) = (q0, , L)
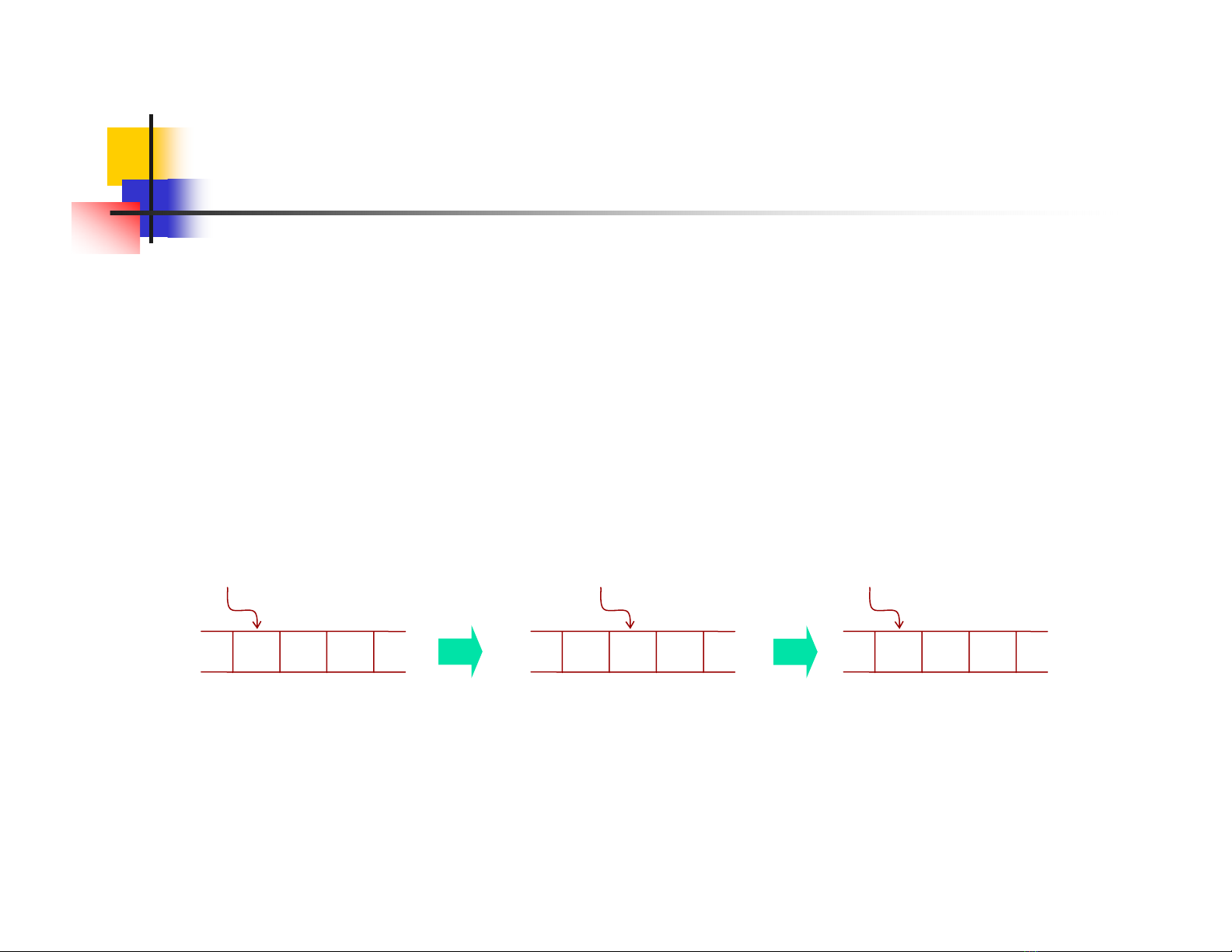
Xét hoạt động của M trong trường hợp sau
Trường hợp này máy không dừng lại và rơi vào một vòng lặp
vô tận(infinite loop)
ab ab
q0q1
ab
q0