Bµi gi¶ng Nguyªn lý m¸y, Chuyªn ngµnh C¬ khÝ chÕ t¹o Lª Cung, Khoa S− ph¹m Kü thuËt
163
1) Cấu tạo
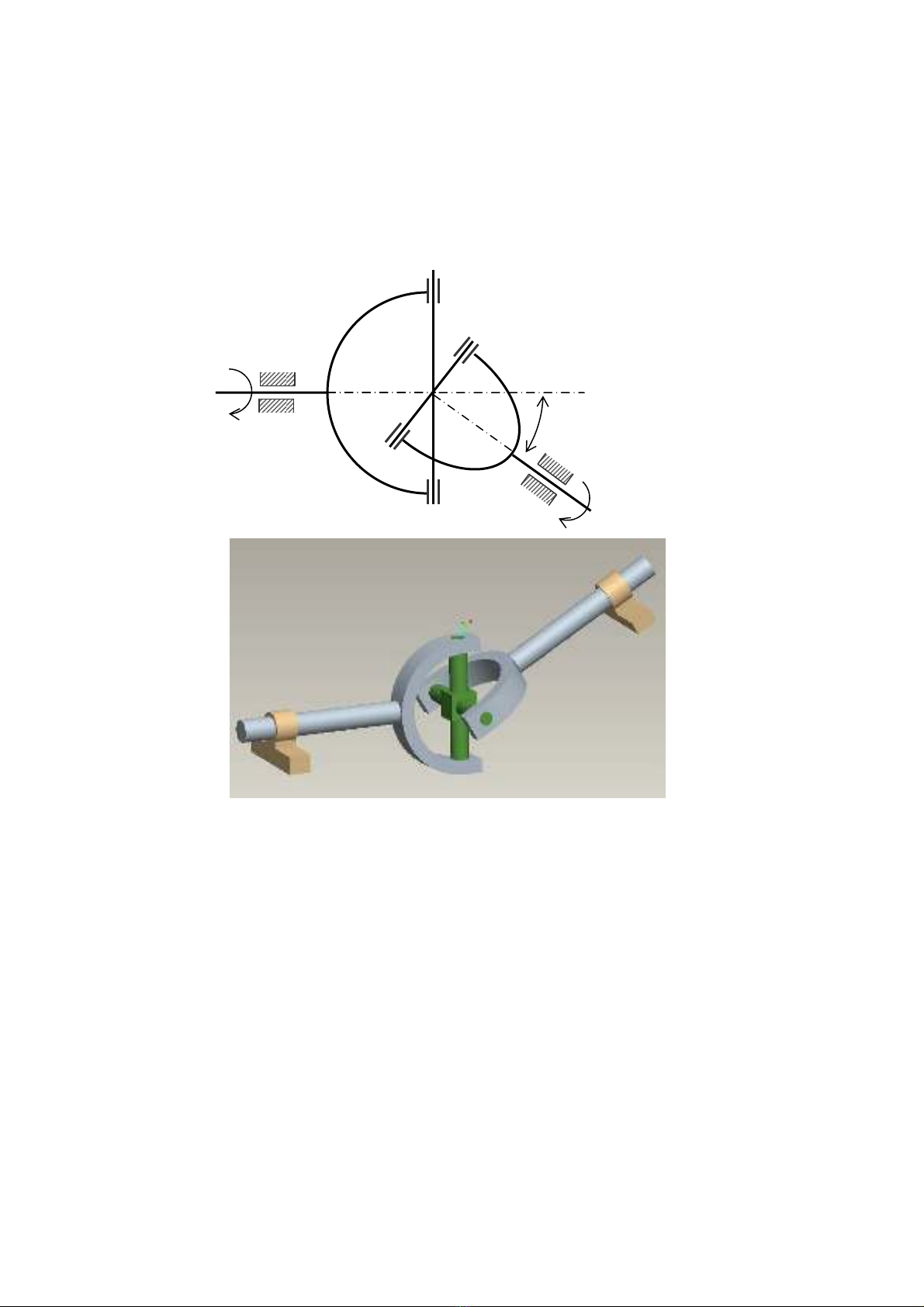
L−îc ®å cÊu t¹o cña c¬ cÊu c¸c ®¨ng cho trªn h×nh 14.5. Hai trôc (1) vµ (2) giao nhau t¹i O
vµ hîp víi nhau mét gãc
α
. Mçi ®Çu trôc mang mét ch¹c (a) vµ (b). Hai ch¹c nµy ®−îc nèi
víi nhau th«ng qua kh©u h×nh ch÷ thËp (3) b»ng c¸c khíp quay A, A’ vµ B, B’. AA’ vu«ng
gãc víi trôc (1). BB’ vu«ng gãc víi trôc (2). AA’ vu«ng gãc víi BB’.
Khi kh©u (1) quay trßn th× kh©u (2) còng quay trßn, cßn kh©u ch÷ thËp (3) chuyÓn ®éng
phøc t¹p quanh ®iÓm O.
2) Phân tích động học
•
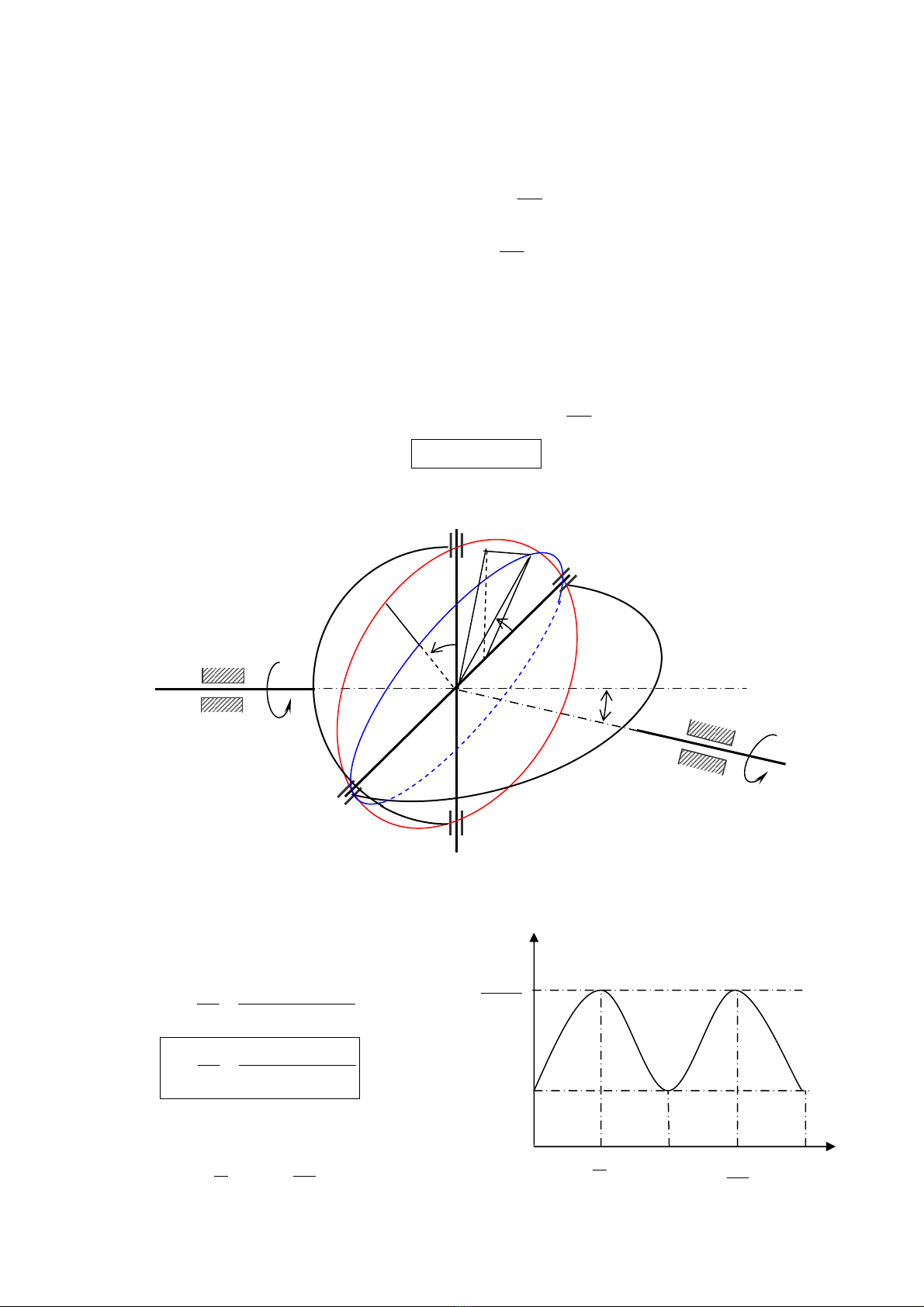
Gäi
α
lµ gãc hîp bëi trôc (1) vµ trôc (2) (h×nh 14.6). Trªn h×nh 14.6, trôc (1) vµ trôc (2) t¹o
nªn mÆt ph¼ng th¼ng ®øng. VÞ trÝ ban ®Çu cña AA’ n»m trong mÆt ph¼ng vu«ng gãc víi mÆt
ph¼ng chøa trôc (1) vµ trôc (2). VÞ trÝ ban ®Çu cña BB’ n»m trong mÆt ph¼ng chøa trôc (1) vµ
trôc (2).
Khi trôc (1) quay, A vµ A’ v¹ch nªn vßng trßn (C
A
) vu«ng gãc víi trôc (1). Khi ®ã B vµ B’
v¹ch nªn vßng trßn (C
B
) vu«ng gãc víi trôc (2). Khi ®iÓm A di chuyÓn trªn vßng trßn (C
A
)
®Õn vÞ trÝ míi lµ A
1
, th× trªn vßng trßn (C
B
), ®iÓm B còng cã vÞ trÝ míi lµ B
1
. AA’ lµ giao tuyÕn
cña c¸c mÆt ph¼ng chøa vßng trßn (C
A
) vµ (C
B
).
Gãc quay cña kh©u (1) vµ kh©u (2) lÇn l−ît lµ
(
)
11
,OA OA
θ
=
J
JJGJJJG
vµ
(
)
21
,OB OB
θ
=JJJG JJJG
.
Tõ A
1
h¹ A
1
H vu«ng gãc víi mÆt ph¼ng cña vßng trßn (C
B
), tõ H h¹ HI vu«ng gãc víi AA’.
Theo ®Þnh lý ba ®−êng vu«ng gãc, ta suy ra :
1
'AI AA
⊥
.
α
H
×nh 14.5: C¬ cÊu c¸c ®¨ng
A
A’
B
B’
O
Ch¹c (a)
Ch¹c (b)
3
1
2
1
ω
2
Trôc (2)
Trôc (1)
Bµi gi¶ng Nguyªn lý m¸y, Chuyªn ngµnh C¬ khÝ chÕ t¹o Lª Cung, Khoa S− ph¹m Kü thuËt
164
Nh− vËy, gãc
n
1
HIA
chÝnh lµ gãc nhÞ diÖn hîp bëi c¸c mÆt ph¼ng chøa vßng trßn (C
A
) vµ (C
B
).
Do trôc (1) vµ trôc (2) lÇn l−ît vu«ng gãc víi mÆt ph¼ng chøa vßng trßn (C
A
) vµ (C
B
), nªn gãc
n
1
HIA
còng chÝnh lµ gãc gi÷a hai trôc (1) vµ (2) :
n
1
HIA
α
=
.
Dùa vµo tam gi¸c A
1
HI vu«ng t¹i H, ta cã :
1
cos
I
H
I
A
α
= (14.7)
Dùa vµo tam gi¸c OA
1
I vu«ng t¹i I, ta cã :
1
1
I
A
tg OI
θ
= (14.8)
MÆt kh¸c, do
11
OB OA
⊥
(v× chóng lµ vÞ trÝ míi cña hai thanh OA vµ OB lu«n lu«n vu«ng gãc
víi nhau) vµ
1
OB
trùc giao víi
1
HA
(v×
1
HA
vu«ng gãc víi mÆt ph¼ng (C
B
) chøa
1
OB
), nªn
1
OB
vu«ng gãc víi mÆt ph¼ng
1
OHA
. Suy ra :
1
OB OH
⊥
.
Tõ ®ã suy ra r»ng :
n
n
12
AOH BOB
θ
==
(gãc cã c¹nh th¼ng gãc).
Dùa vµo tam gi¸c OIH vu«ng t¹i I, ta cã :
n
2
I
H
tg tg IOH OI
θ
== (14.9)
Tõ (14.7), (14,8) vµ (14.9) suy ra :
12
.costg tg
θ
αθ
=
(14.10)
`
•
§¹o hµm hai vÕ cña (14.10) theo t :
() ()
22
11 2 2
1..cos1.tg tg
θ
ωα θω
+=+
⇒
()
2
12
12 2
21
1
1cos
tg
itg
ωθ
ω
θ
α
+
==
+
⇒
()
22
11
12 2
21
1.cos
1cos
tg
itg
ω
θα
ω
θ
α
+
==
+
• Khi
1
0
θ
=
vµ
1
θ
π
=
th× :
2min 1
cos
ω
ωα
=
.
Khi
1
2
π
θ
= vµ
1
3
2
π
θ
= th× :
H
×nh 14.7
2
ω
1
θ
1
cos
ω
α
1
cos
ω
α
2
π
0
3
2
π
π
2
π
n
1
HIA
α
=
n
11
A
OA
θ
=
n
n
21
B
OB AOH
θ
==
B’
O
(2)
(1)
H
×nh 14.6
ω
2
ω
1
B
A’
A
α
A
1
B
1
θ
2
θ
1
I
(C
B
)
Chạc (a)
(
C
A
)
H
Chạc (b)
Bµi gi¶ng Nguyªn lý m¸y, Chuyªn ngµnh C¬ khÝ chÕ t¹o Lª Cung, Khoa S− ph¹m Kü thuËt
165
1
2max
cos
ω
ω
α
=.
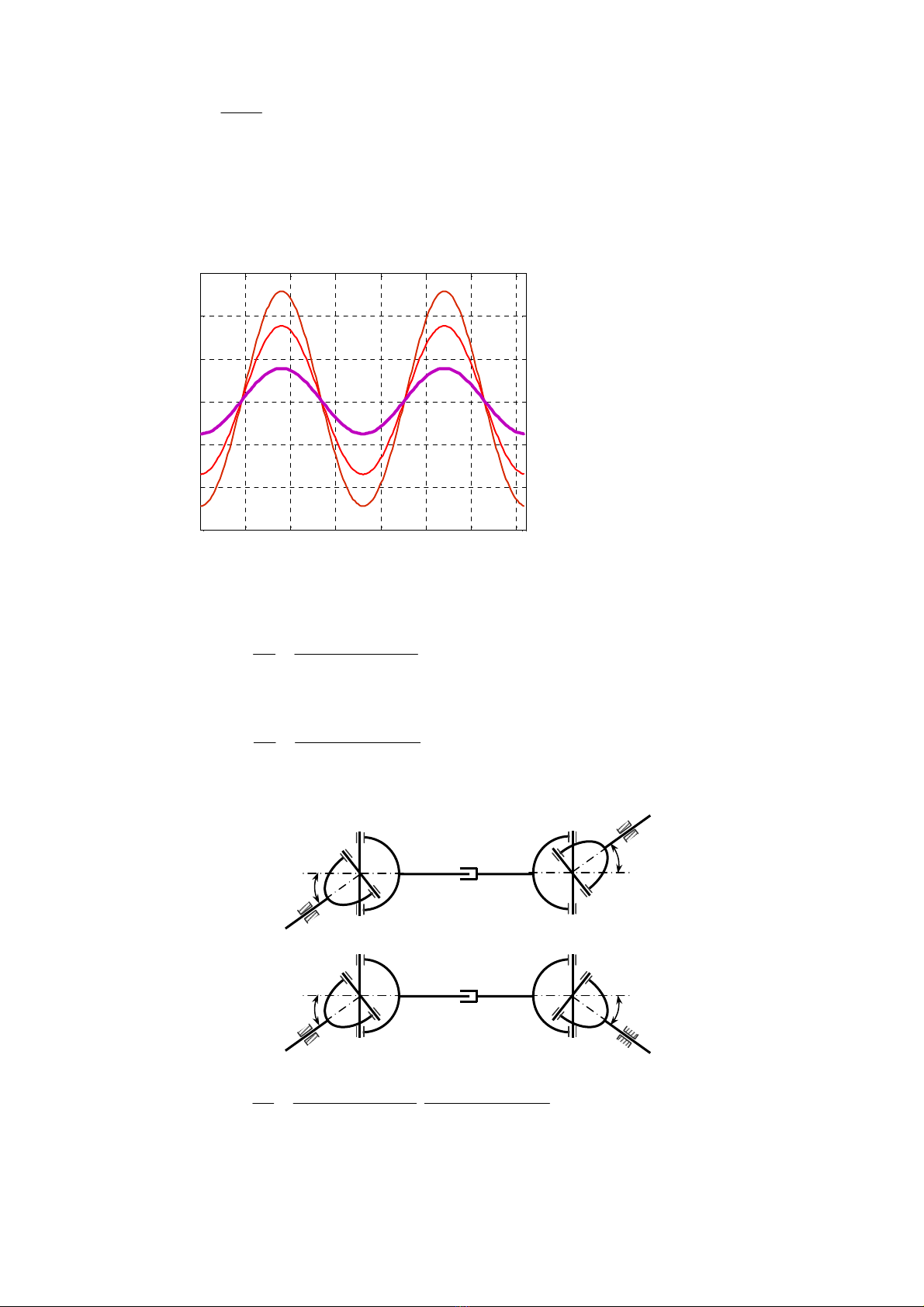
§å thÞ biÓu diÔn
2
ω
theo gãc quay
1
θ
cña trôc (1) cho trªn h×nh 14.7.
• Khi gãc hîp nhau gi÷a hai trôc
0
α
=
th× tû sè truyÒn
12
1i
=
. Khi gãc
0
α
≠
th× tû sè truyÒn
12
i≠
h»ng sè. Khi
α
cµng lín th× biªn ®é dao ®éng cña
2
ω
cµng lín, g©y ra dao ®éng xo¾n
lín trong c¸c bé phËn bÞ dÉn (h×nh 14.8).
3) Cơ cấu các đăng kép
§Ó trôc dÉn (1) vµ trôc bÞ dÉn (3) cã cïng vËn tèc gãc ph¶i dïng c¬ cÊu c¸c ®¨ng kÐp. Trôc (1)
®−îc nèi víi trôc (3) th«ng qua trôc (2) vµ hai khíp c¸c ®¨ng.
Ta cã :
()
22
221
21 2
121
1.cos
1cos
tg
itg
ω
θα
ω
θ
α
+
==
+
Víi
2
θ
gãc quay cña ch¹c (b) tÝnh tõ mÆt ph¼ng vu«ng gãc víi mÆt ph¼ng chøa trôc (2) vµ (1).
()
2, 2
222
23 2,
322
1.cos
1cos
tg
itg
ω
θα
ω
θ
α
+
==
+
Víi
,
2
θ
gãc quay cña ch¹c (b’) tÝnh tõ vu«ng gãc víi mÆt ph¼ng chøa trôc (2) vµ (1).
Do ®ã:
()
()
22, 2
21
122
13 22 2,
321
22
1cos
1.cos
.
1.cos
1cos
tg tg
itg tg
θα
ω
θα
ωθα
θ
α
++
==
++
§Ó i
13
b»ng h»ng sè, ph¶i cã hai ®iÒu kiÖn :
+
12
α
α
=
+
,
22
θ
θ
=
(hai gãc quay cña hai ®Çu ch¹c n»m trªn trôc (2) ph¶i b»ng nhau).
050 100 150 200 250 300 350
94
96
98
100
102
104
106
H×nh 14.8
§å thÞ biÓu diÔn sù biÕn
thiªn cña vËn tèc gãc
ω
2
theo gãc quay
θ
1
cña kh©u
dÉn øng víi c¸c gi¸ trÞ kh¸c
nhau cña gãc
α
gi÷a hai trôc
quay (
ω
1
=100 Rad/s)
α
=10
0
α
=18
0
α
=5
0
2
[/]
R
ad s
ω
1
θ
1
2
H
×nh 14.10
α
2
3
b
α
1
b’
1
2
H×nh 14.9
b
α
1
α
2
b’ 3
Bµi gi¶ng Nguyªn lý m¸y, Chuyªn ngµnh C¬ khÝ chÕ t¹o Lª Cung, Khoa S− ph¹m Kü thuËt
166
Nh− vËy, trong tr−êng hîp trôc (1) vµ trôc (3) n»m trong cïng mét mÆt ph¼ng (trôc (1) vµ (3)
song song nh− trªn h×nh 14.9 hay c¾t nhau nh− trªn h×nh 14.10) th× hai ch¹c (b) vµ (b’) cña
trôc (2) ph¶i n»m trªn cïng mét mÆt ph¼ng.
§3. Cơ cấu Man
C¬ cÊu Man ®−îc dïng ®Ó truyÒn chuyÓn ®éng quay liªn tôc cña kh©u dÉn thµnh chuyÓn
®éng quay gi¸n ®o¹n lóc quay lóc dõng cã chu kú cña kh©u bÞ dÉn. C¬ cÊu Man ®−îc dïng
trong c¬ cÊu thay dao cña m¸y tù ®éng, c¬ cÊu cÊp ph«i tù ®éng, c¬ cÊu ®−a phim cña m¸y
chiÕu phim...
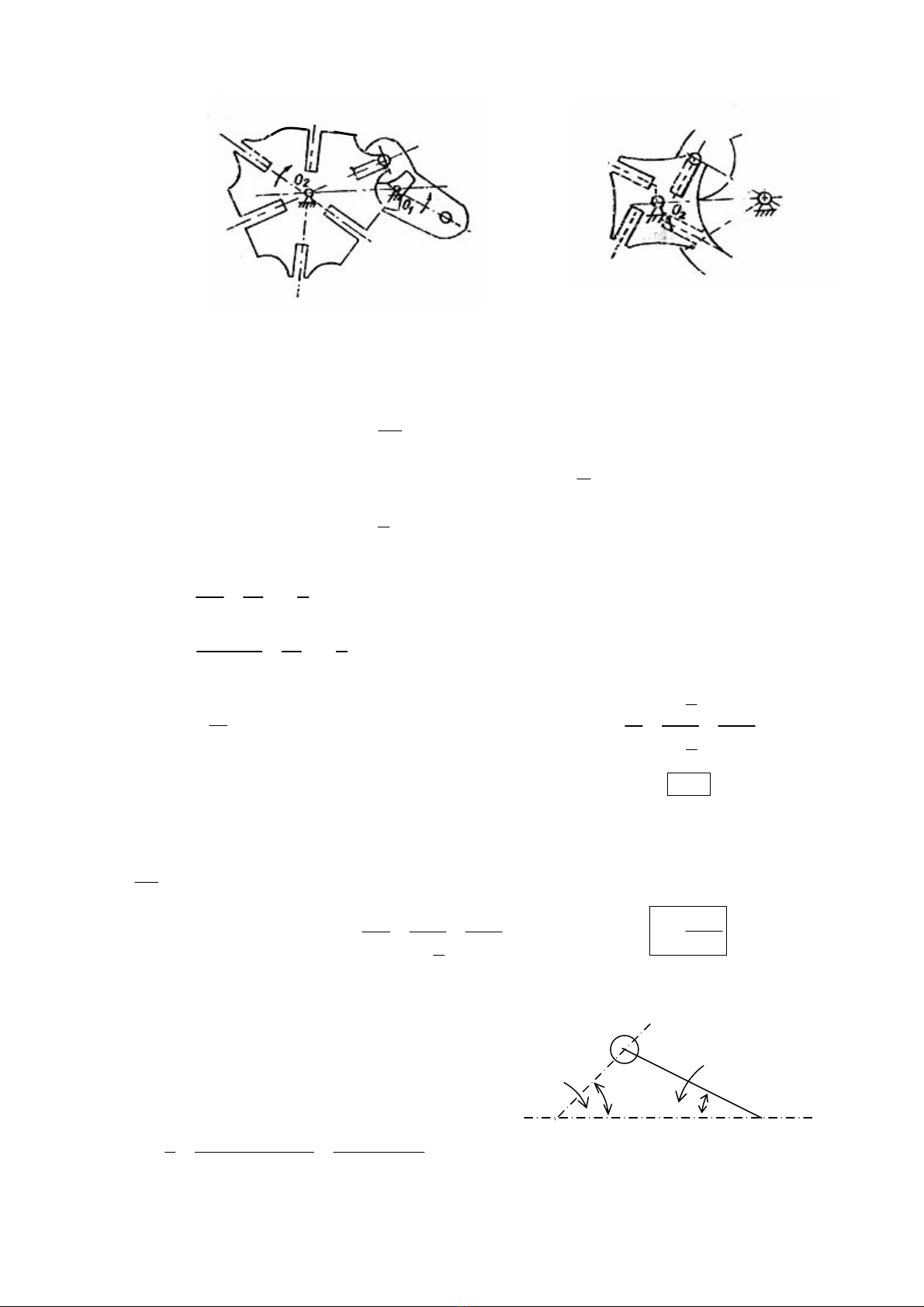
1) Cấu tạo
¾ C¬ cÊu Man ngo¹i tiÕp gåm mét ®Üa trßn (1) cã l¾p chèt A, vµ ®Üa h×nh sao (2) cã nhiÒu
r·nh h−íng t©m ®èi xøng qua t©m O
2
. Khi ®Üa (1) quay, cã lóc chèt A lät vµo mét r·nh cña ®Üa
(2), khi ®ã ®Üa (2) quay quanh O
2
. Khi chèt A ra khái r·nh nµy, ®Üa (2) dõng l¹i. Khi chèt A
tiÕp tôc ®i vµo r·nh kÕ tiÕp trªn ®Üa (2), ®Üa (2) l¹i quay quanh O
2
.
§Ó tr¸nh chuyÓn ®éng quay ngÉu nhiªn cña ®Üa (2) do t¸c ®éng cña c¸c momen ngÉu
nhiªn trong kho¶ng thêi gian tõ khi chèt A ra khái mét r·nh cña ®Üa (2) ®Õn khi chèt A ®i vµo
r·nh kÕ tiÕp trªn ®Üa (2), th× trong kho¶ng thêi gian nãi trªn, ta ph¶i khãa cøng ®Üa (2) l¹i nhê
cung trßn cña ®Üa (1) cµi vµo cung trßn EDC trªn ®Üa (2) (h×nh 14.11).
Sè chèt trªn ®Üa (1) cã thÓ b»ng 1 hay lín h¬n 1. Sè r·nh trªn ®Üa (2) th−êng lµ 4, 6, 8.
¾ Ghi chó
C¸c chèt vµ c¸c r·nh trªn c¬ cÊu Man cã thÓ ph©n bè bÊt kú (kho¶ng c¸ch tõ t©m c¸c chèt
®Õn t©m O
2
cã thÓ kh«ng b»ng nhau nh− trªn h×nh 14.12, c¸c r·nh cña ®Üa (2) cã thÓ kh«ng
h−íng t©m nh− trªn h×nh 14.11), miÔn lµ chóng phèi hîp ®−îc víi nhau.
O
1
C
2
ω
O
2
(2)
D
E
1
ω
(1)
2
2
ϕ
1
2
ϕ
Ê
A
H
×nh 14.11
Bµi gi¶ng Nguyªn lý m¸y, Chuyªn ngµnh C¬ khÝ chÕ t¹o Lª Cung, Khoa S− ph¹m Kü thuËt
167
2) Phân tích động học
a) Số rãnh tối thiểu - Số chốt tối đa
• Trªn h×nh 14.11, ta cã:
2
2
2z
π
ϕ
= víi z sè r·nh cña ®Üa.
§Ó chèt A kh«ng bÞ va ®Ëp khi ®i vµo trong r·nh :
n
21
OAO z
π
=
Suy ra :
12
2
22(1)
z
ϕπ ϕπ
=− = −
Gäi t
C
lµ thêi gian chuyÓn ®éng cña ®Üa (2); t
D
lµ thêi gian dõng cña ®Üa (2):
1
11
22
1
C
tz
ϕπ
ωω
⎛⎞
== −
⎜⎟
⎝⎠
1
11
22 2
1
D
tz
πϕπ
ωω
−⎛⎞
==+
⎜⎟
⎝⎠
víi :
1
ω
lµ vËn tèc gãc cña ®Üa (1) :
1
ω
= h»ng sè
Tû sè
C
D
t
kt
= gäi lµ hÖ sè thêi gian chuyÓn ®éng cña c¬ cÊu:
2
12
22
1
C
D
tz
z
ktz
z
−−
== =
+
+
V× k > 0 vµ z nguyªn nªn
3z≥
hay sè r·nh tèi thiÓu trong c¬ cÊu Man :
3z=
• §Ó t¨ng sè lÇn chuyÓn ®éng cña ®Üa (2), øng víi mét vßng quay cña ®Üa (1), cã thÓ t¨ng sè
chèt trªn ®Üa (1). Gäi m lµ sè chèt, gãc ë t©m nhá nhÊt t¹o gi÷a hai chèt ph¶i b¶o ®¶m :
1
22
m
π
ϕ
≥(tøc khi chèt A ra khái r·nh cña ®Üa (2) th× chèt kÕ tiÕp trªn ®Üa (1) míi ®−îc vµo
khíp víi ®Üa (2)) . Hay :
1
222
2
22
1
z
mz
z
π
ϕ
≤= =
−
−
⇒
Sè chèt tèi ®a: 2
2
z
mz
=−
b) Tỷ số truyền
§Ó x¸c ®Þnh vËn tèc vµ gia tèc cña ®Üa (2) ta
xÐt mét vÞ trÝ bÊt kú cña c¬ cÊu, khi ®ã tay quay
O
1
A vµ r·nh O
2
A cña ®Üa t¹o víi ®−êng trôc O
1
O
2
c¸c gãc lÇn l−ît lµ
1
ϕ
vµ
2
ϕ
(h×nh 14.14)
Trong tam gi¸c O
1
AO
2
, ta cã
:
()()
22
21 21
sin sin
sin sin
r
l
ϕ
ϕ
λ
π
ϕϕ ϕϕ
== =
−− +
Trong ®ã :
12 1
,
OO O A
ll rl==
1
O
H
×nh 14.12
H
×nh 14.13
O
1
2
ω
O
2
1
ω
2
ϕ
1
ϕ
Hình 14.14
A
l
r