Bài giảng Sức bền vật liệu: Chương 3 - TS. Trần Minh Thi

Tài liệu này giới thiệu Chương 3 về thanh chịu kéo (hay nén) đúng tâm, một khái niệm cơ bản trong Sức bền vật liệu. Nó bao gồm định nghĩa, ứng suất, biến dạng, các thí nghiệm vật liệu, thế năng biến dạng đàn hồi, điều kiện bền và bài toán siêu tĩnh liên quan đến loại cấu kiện này.

Tài liệu này hướng đến sinh viên, kỹ sư và những người học chuyên ngành kỹ thuật, đặc biệt là các ngành Xây dựng, Cơ khí, Vật liệu hoặc bất kỳ ai đang nghiên cứu về Sức bền vật liệu và Cơ học vật liệu.

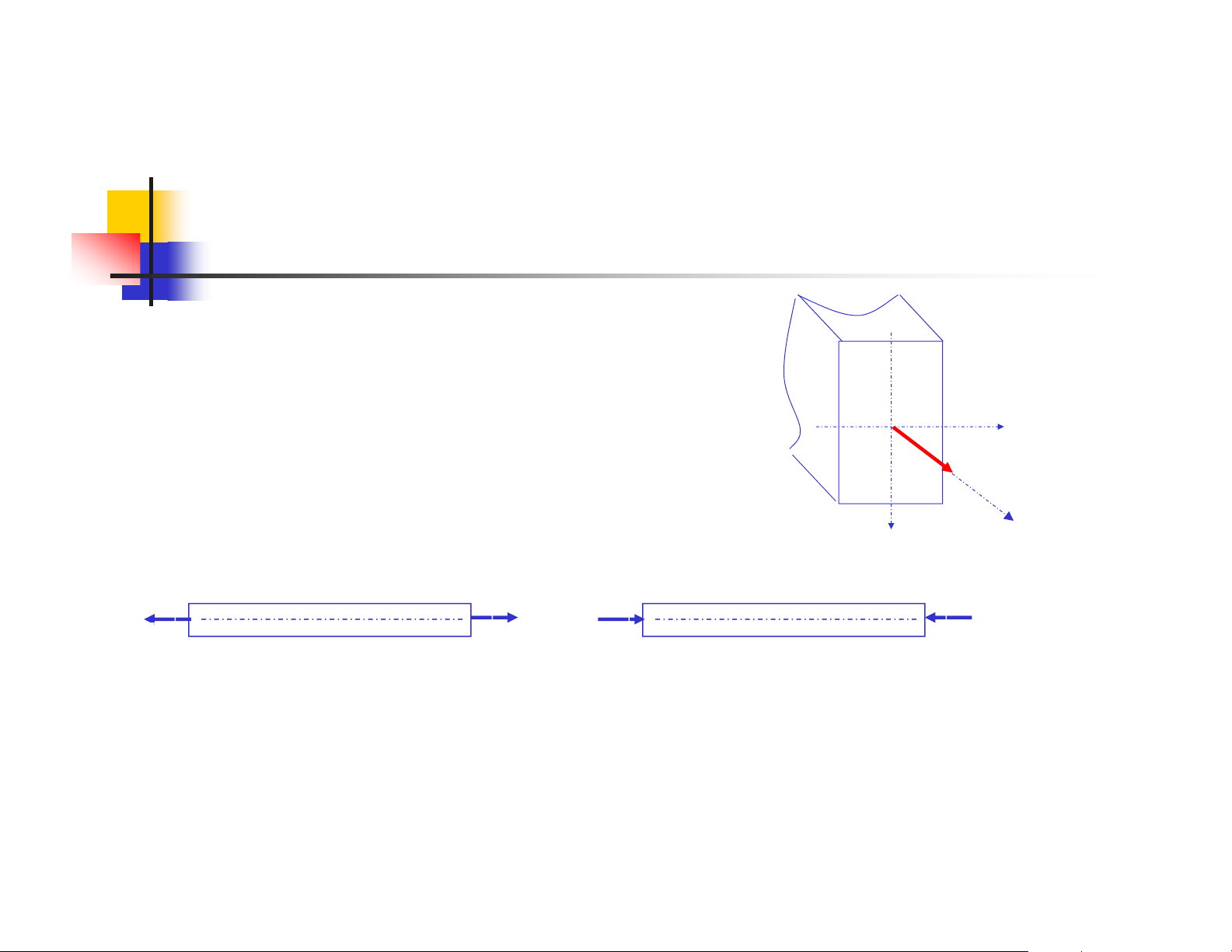
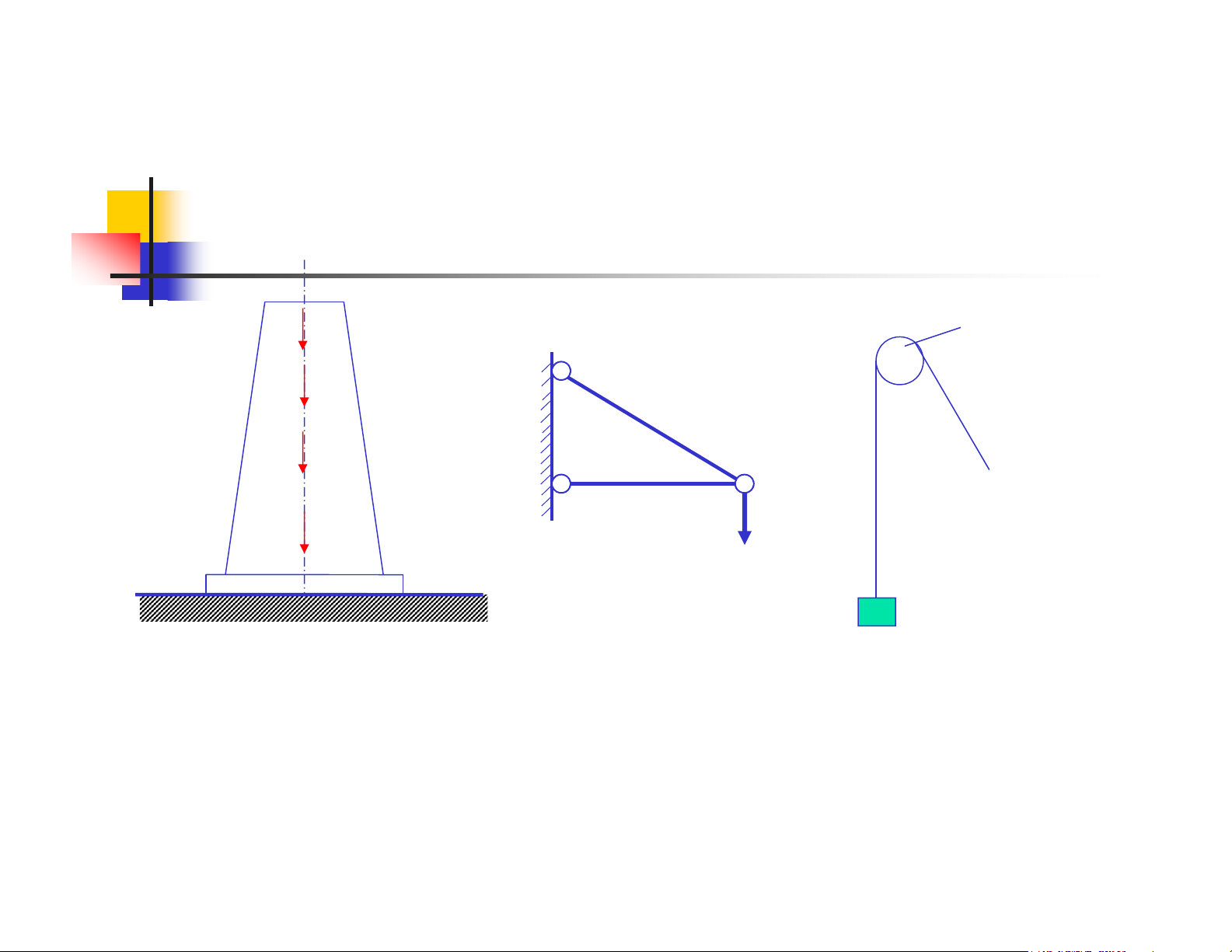
Tài liệu này trình bày chi tiết Chương 3 về thanh chịu kéo hoặc nén đúng tâm, một nội dung cốt lõi trong ngành Cơ học vật liệu và Sức bền vật liệu. Mở đầu, tài liệu định nghĩa thanh chịu lực đúng tâm và minh họa bằng các ví dụ thực tế như dây treo vật nặng hay các cấu kiện trong hệ dàn. Tiếp theo, tài liệu đi sâu vào phân tích ứng suất pháp trên mặt cắt ngang của thanh, giải thích công thức tính ứng suất và tính chất phân bố đều của nó. Phần biến dạng làm rõ khái niệm biến dạng dọc trục, biến dạng dài tương đối, mối quan hệ giữa ứng suất và biến dạng thông qua định luật Hooke và môđun đàn hồi E. Đặc biệt, tài liệu còn giới thiệu hệ số Poisson và vai trò của nó trong việc mô tả biến dạng ngang của vật liệu dưới tác dụng của tải trọng dọc trục. Các thí nghiệm vật liệu, bao gồm thí nghiệm kéo và nén đối với vật liệu dẻo (như thép) và vật liệu dòn (như gang), được trình bày chi tiết để phân tích đặc trưng chịu lực, các giai đoạn biến dạng (đàn hồi, chảy, củng cố) và các giới hạn bền, chảy, tỉ lệ. Tài liệu cũng đề cập đến thế năng biến dạng đàn hồi tích lũy trong thanh khi chịu tải trong giới hạn đàn hồi, đưa ra các công thức tính toán và ứng dụng. Cuối cùng, tài liệu trình bày điều kiện bền cho thanh chịu kéo/nén đúng tâm, bao gồm khái niệm ứng suất cho phép, hệ số an toàn và các bài toán cơ bản như kiểm tra bền, định kích thước mặt cắt ngang và xác định tải trọng cho phép. Phần cuối cùng giải thích về bài toán siêu tĩnh, một loại bài toán mà các phương trình cân bằng tĩnh học không đủ để giải, và phương pháp giải quyết chúng bằng cách bổ sung các phương trình điều kiện biến dạng.