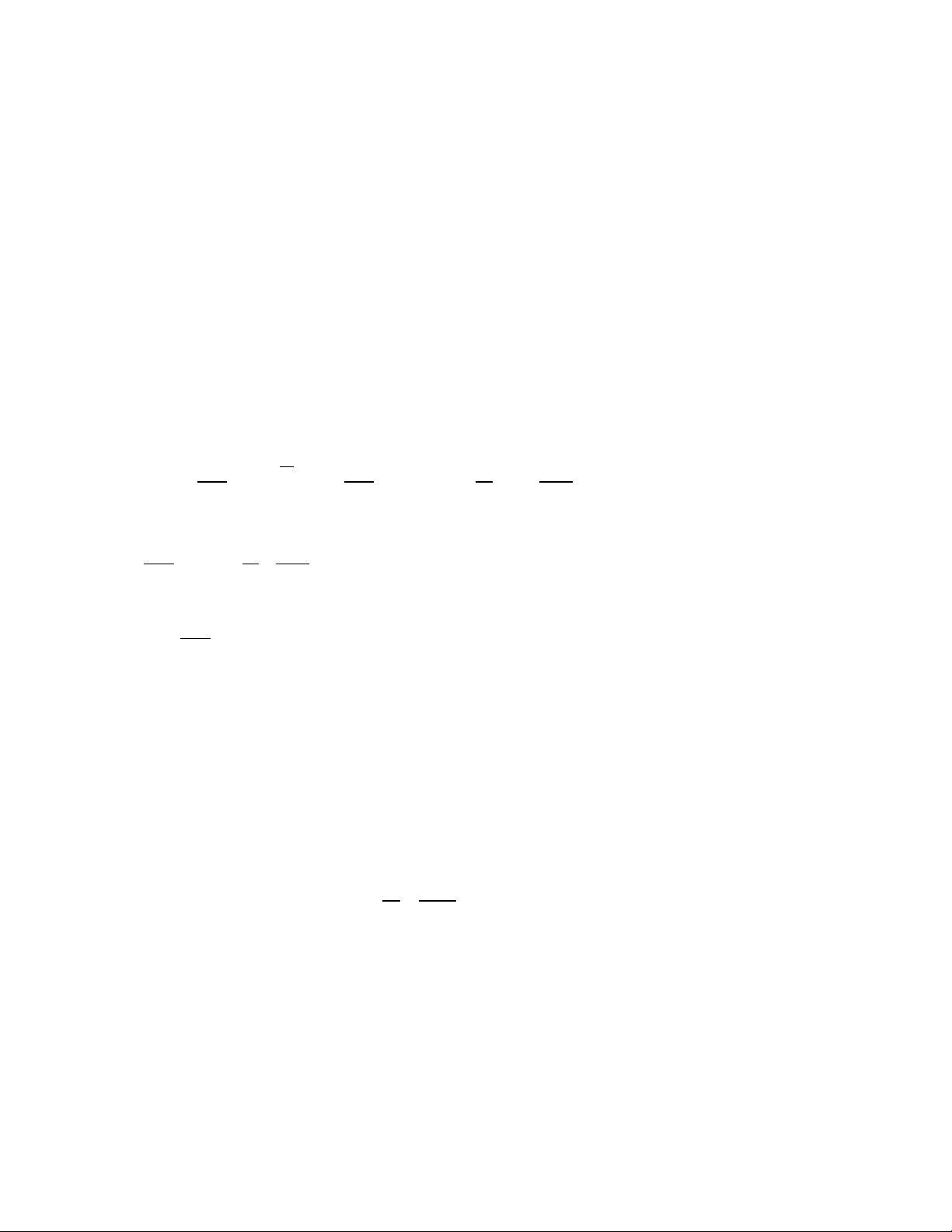PH N I :M ĐUẦ Ở Ầ
I. N I DUNG NGHIÊN C UỘ Ứ
-Nghiên c u v bi u th c c a hàm nhi t đng theo tích phân tr ng tháiứ ề ể ứ ủ ệ ộ ạ
_Tích phân tr ng thái và các hàm nh t đng c a khí lý t ngạ ệ ộ ủ ưở
_Bài t p v ph n tích phân tr ng thái và các hàm nhi t đngậ ề ầ ạ ệ ộ
II. M C ĐÍCH NGHIÊN C UỤ Ứ
_ Nghiên c u v bi u th c c a hàm nhi t đng theo tích phân tr ng ứ ề ể ứ ủ ệ ộ ạ
thái đ th y r b n ch t ý nghĩa c a nó.ể ấ ỏ ả ấ ủ
_ Nghiên c u v bi u th c c a hàm nhi t đng theo tích phân tr ng ứ ề ể ứ ủ ệ ộ ạ
thái đ th y m i quan h gi a chúngể ấ ố ệ ử
III. PH NG PHÁP NGHIÊN C UƯƠ Ứ
_Thu th p tài li u có liên quan t i nghiên c u v bi u th c c a hàm ậ ệ ớ ứ ề ể ứ ủ
nhi t đng theo tích phân tr ng tháiệ ộ ạ
_Đc và l a ch n n i dungọ ự ọ ộ
_T ng h p n i dungổ ợ ộ
_B sung s a ch a n i dung ổ ử ử ộ
PH N 2: N I DUNGẦ Ộ
A: LÝ THUY TẾ
TÍCH PHÂN TR NG THÁI VÀ CÁC HÀM NHI T ĐNGẠ Ệ Ộ
I: Bi u th c c a các hàm nhi t đng theo tích phân tr ng tháiể ứ ủ ệ ộ ạ
Trong ch ng tr c chúng ta đã tìm hi u đc m t h th c c b n c a ươ ướ ể ượ ộ ệ ứ ơ ả ủ
nhi t đng l c h c th ng kê di n t m i quan h c a năng l ng t do ệ ộ ứ ọ ố ễ ả ỗ ệ ủ ượ ự
ψ
c a h v i tích phân tr ng thái Zủ ệ ớ ạ
lnkT Z
ψ
=−
(6.1)
T đó chúng tacos th bi u di n các thong s nhi t đng và hàm ừ ể ể ễ ố ệ ộ
nhi t đng b t k c a h theo tích phân tr ng thái Z,đi u đó cho phép ta ệ ộ ấ ỳ ủ ệ ạ ề
xác đnh đc nhi u tính ch t c a h nhi t đng.Vi c tìm l i cacsn h ị ượ ề ấ ủ ệ ệ ộ ệ ạ ệ
th c nhi t đng và tính các hàm nhi t đng theo các thông s vi mô c a ứ ệ ộ ệ ộ ố ủ
h chính là n i dung c b n c a nhi t đng l c h c th ng kê.ệ ộ ơ ả ủ ệ ộ ự ọ ố
Đu tiên chúng ta hãy tìm áp su t p đc xác đnh qua năng l ng t ầ ấ ượ ị ượ ự
do
ψ
theo công th c ứ
T
pV
ψ
= −
(6.2)
Áp d ng công th c (6.1) ta thu đcụ ứ ượ
p = kT
ln
T
Z
V
(6.3)
Đó là ph ng trình tr ng thái c a h .b i vì th ph i c a (6.3) ph ươ ạ ủ ệ ở ế ả ủ ụ
thu c vào V và T.Ta có th vi t l i ph ng trình tr ng thái (6.3) d i ộ ể ế ạ ươ ạ ướ
d ng quen thu c h n b ng cách nhân hai v c a đng th c v i Vạ ộ ơ ằ ế ủ ẳ ứ ớ
ln
ln
T
Z
pV V
=
(6.4)
T ph ng trình Gipxow-Hemhừ ươ onxo chúng ta tính đc n i năng Uượ ộ
( )
2
ln ln
ln ln
V V V
Z Z
U T kT Z k Z T kT kT
T T T
Ψ
= Ψ − = − + + =
(6.5)
M t cách t ng t , ta có th tính các hàm nhi t đng khác nh th nhi t ộ ươ ự ể ệ ộ ư ề ệ
đng Gipx , entanpy và entropy theo các tích phân tr ng thái. Nh v y ta ộ ơ ạ ư ậ
th y r ng t t c các hàm nhi t đng đc bi u th theo tích phân tr ng ấ ằ ấ ả ệ ộ ượ ể ị ạ
thái Z. Nh ng th c t dù cho có bieets đc hàm phân b trong không gianư ự ế ượ ố
pha thì vi c tính tích phân tr ng thái cũng t ng đi khó, b i vì Z đc ệ ạ ươ ố ở ượ
tính b ng m t tích phân ph c t pằ ộ ứ ạ
1 2 3 , 1 2 3
1 2 3 1 3
( , ... , ... ,
... exp * ... ...
N N
N N
H q q q p p p a
Z dq dq dq dp dp
θ
+
−
*
= −
�
(6.6)
Vì v y, trong tr ng h p t ng quát, vi c tính tích phân tr ng thái là r t ậ ườ ợ ổ ệ ạ ấ
ph c t p, và ch đi v i h đn gi n phép tính đó m i đc ti n hành ứ ạ ỉ ố ớ ệ ơ ả ớ ượ ề
thành công. Trong nh ng tr ng h p khi mà ta không th tính đc tích ữ ườ ợ ể ượ
phân tr ng thái m t cách chính xác, chúng ta s s d ng ph ng pháp g nạ ộ ẽ ử ụ ươ ầ
đúng
Trong tr ng h p đc bi t, tích ườ ợ ặ ệ phân tr ng thái th ng có tính ch t ạ ườ ấ
nhân
1 2
...
k
Z Z Z Z
=
Nghĩa là tích phân tr ng thái c a toàn b h có th bi u th nh là tích c aạ ủ ộ ệ ể ể ị ư ủ
các tích phân tr ng thái c a các ph n đc l p c a h .Th c v y, n u nh ạ ủ ầ ộ ậ ủ ệ ự ậ ế ư
ta có th chia các h kh o sát ra thành các ph n đc l p đi v i nhau ể ệ ả ầ ộ ậ ố ớ
(nghĩa là b qua năng l ng t ng tác gi a các ph n đó), thì năng l ng ỏ ượ ươ ữ ầ ượ
c a toàn b h s b ng t ng năng l ng c a các ph n đc l p đó.Gi s ủ ộ ệ ẽ ằ ổ ượ ủ ầ ộ ậ ả ử
h g m hai ph n đc l p A và B ta cóệ ồ ầ ộ ậ
Do đó
( ) ( )
*
AB A B
AB A B
H H H
A B
X X X
e dX e dX e dX
θ θ θ
− − −
=
Nghĩa là
AB A B
Z Z Z
=
M r ng quy t c đó ra cho m t s b t kì k ph n đc l p c a h chúng ở ộ ắ ộ ố ấ ầ ộ ậ ủ ệ
ta thu đc (6.7)ượ
II : Tích phân tr ng thái và các hàm nhi t đng c a khí lý t ng.ạ ệ ộ ủ ưở
Áp d ng phân b chính t c ụ ố ắ
( , ) ( , )
( ) exp a H X a
X
ψθ
ωθ
−
*
=�
chúng ta hãy tính m t s hàm nhi t đng c a khí lý t ng.ộ ố ệ ộ ủ ưở
1) Đ tính tích phân tr ng thái Z ta c n bi t hàm Haminton H .Đi ể ạ ầ ế ố
v i khí lí t ng,hàm Haminton b ng t ng các năng l ng c a các ớ ưở ằ ổ ượ ủ
h t riêng l ,nghĩa làạ ẻ
2
1
( )
2
N
k
k
k
p
H U X
m
=
= +
(6.8)
đây Ở
( )
k
U X
bi u th th năng c a h t th k,mà chúng ta đa vàoể ị ế ủ ạ ứ ư
xu t phát t l p lu n sau đây .Các h t c a khí lí t ng có th chuy n ấ ừ ậ ậ ạ ủ ưở ể ể
đng hoàn toàn tùy ý bên trong bình có th tich V nh ng chúng không ộ ể ư
th ra kh i gi i h n c a bình .Đi u đó t ng đng v i gi thi t là: ể ỏ ớ ạ ủ ề ươ ươ ớ ả ế
bên trong bình các h t có th năng b ng không,còn ngoài bình ở ạ ế ằ ở
chúng có th năng vô cùng l n (hình 6.1) ( đây gi thi t không có ế ớ Ở ả ế
các tr ng l c ngoài tác d ng lên các h t c a khí lí t ng).ườ ự ụ ạ ủ ưở
Nh v y,chúng ta có th đa thông s ngo i V vào hàm ư ậ ể ư ố ạ
Haminton H(X,a) thông qua th năng U(x,y,z) mà ta có th bi u th ế ể ể ị
d i d ngướ ạ
U(x,y,z)=
{
0 i v i X b n trong V
i v i X b n trong V
đê
đê
n n
n n
B i vì t t c các h t là đc l p,chúng ta có th vi t tích phân ở ấ ả ạ ộ ậ ể ế
tr ng thái d i d ngạ ướ ạ
2
0
( ) ( )
2
1 1 1
exp
! ! 2
1 1 ( , , ) *
! 2
1
!
x y z
HdX k
k
k
X X
k
k k k k k k k k k k
N
k
p
Z e U dX
N N m
pU x y z dp dp dp dx dy dz
N m
ZN
θ
θ
θ
−
+
−
*
= = − + =
�

*
− + =

�


((6.10)
V i ớ
k
Z
là tích phân tr ng thái đi v i m t h t.chúng ta hãy xét bi u th cạ ố ớ ộ ạ ể ứ
c a ủ
k
Z
m t cách chi ti t h nộ ế ơ
2
1
exp *
2
x y z
k
k k k k k k k k
p
Z U dp dp dp dx dy dz
m
θ
+
−
*
= − +
�
(6.11)
Do tính đc l p c a các hình chi u pộ ậ ủ ế x, py và pz chúng ta có th vi t l iể ế ạ
(6.11) d i d ng:ướ ạ