1
Chƣơng 2. HỆ PHƢƠNG TRÌNH TUYẾN TÍNH
NỘI DUNG:
2.1. Định nghĩa
2.2. Phƣơng pháp giải
2.3. Định lý Kronecker-Capelli
Toán Cao Cấp - ThS. Lê Trường Giang
2
Chƣơng 2. HỆ PHƢƠNG TRÌNH TUYẾN TÍNH
2.1. ĐỊNH NGHĨA
Hệ phương trình tuyến tính là một hệ gồm m phương
trình và n ẩn số có dạng:
Trong đó:
được gọi là các hệ số.
được gọi là các hệ số.
được gọi là các hệ số tự do.
Toán Cao Cấp - ThS. Lê Trường Giang
3
11 1 12 2 1n n 1
21 1 22 2 2n n 2
m1 1 m2 2 mn n m
a x a x a x b
a x a x a x b I
.............................................
a x a x a x b
j
x j 1,n
ij
a i 1,m; j 1,n
i
b , i 1,m
Chƣơng 2. HỆ PHƢƠNG TRÌNH TUYẾN TÍNH
Hệ phương trình tuyến tính còn được viết dưới dạng ma
trận như sau:
Trong đó:
Toán Cao Cấp - ThS. Lê Trường Giang
4
AX B
11 12 1n
21 22 2n
m1 m2 mn
11
22
mn
a a a
a a a
A
a a a
bx
bx
B ; X
bx

Chƣơng 2. HỆ PHƢƠNG TRÌNH TUYẾN TÍNH
Các hệ phương trình đặc biệt:
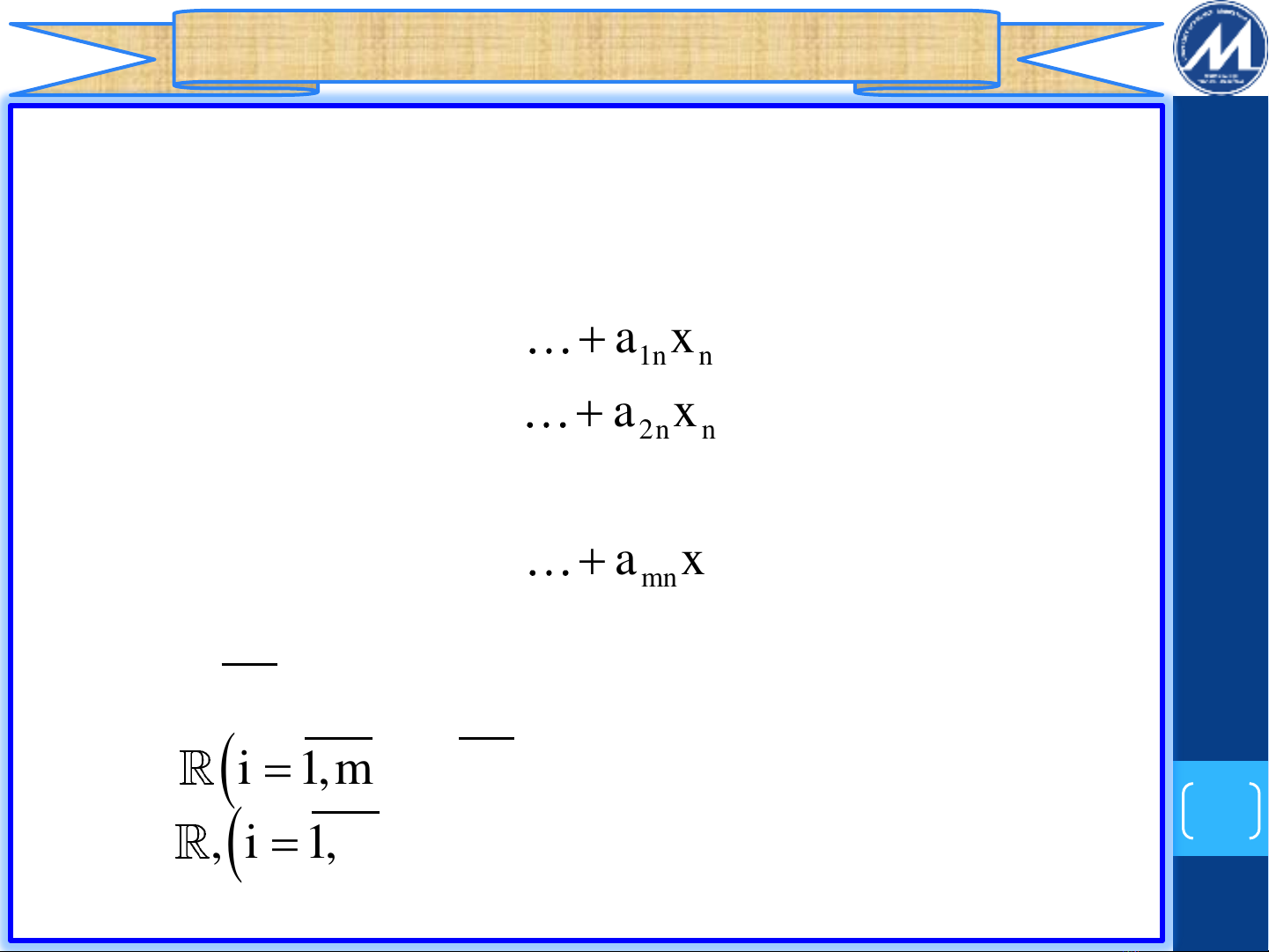
1) Nếu thì ta gọi (I) là hệ phương trình
tuyến tính thuần nhất.
2) Nếu và thì ta gọi (I) là hệ Cramer.
2.2. PHƢƠNG PHÁP GIẢI
1) Đối với hệ phương trình tổng quát
Ta giải hệ phương trình theo phương pháp Gauss, tức là
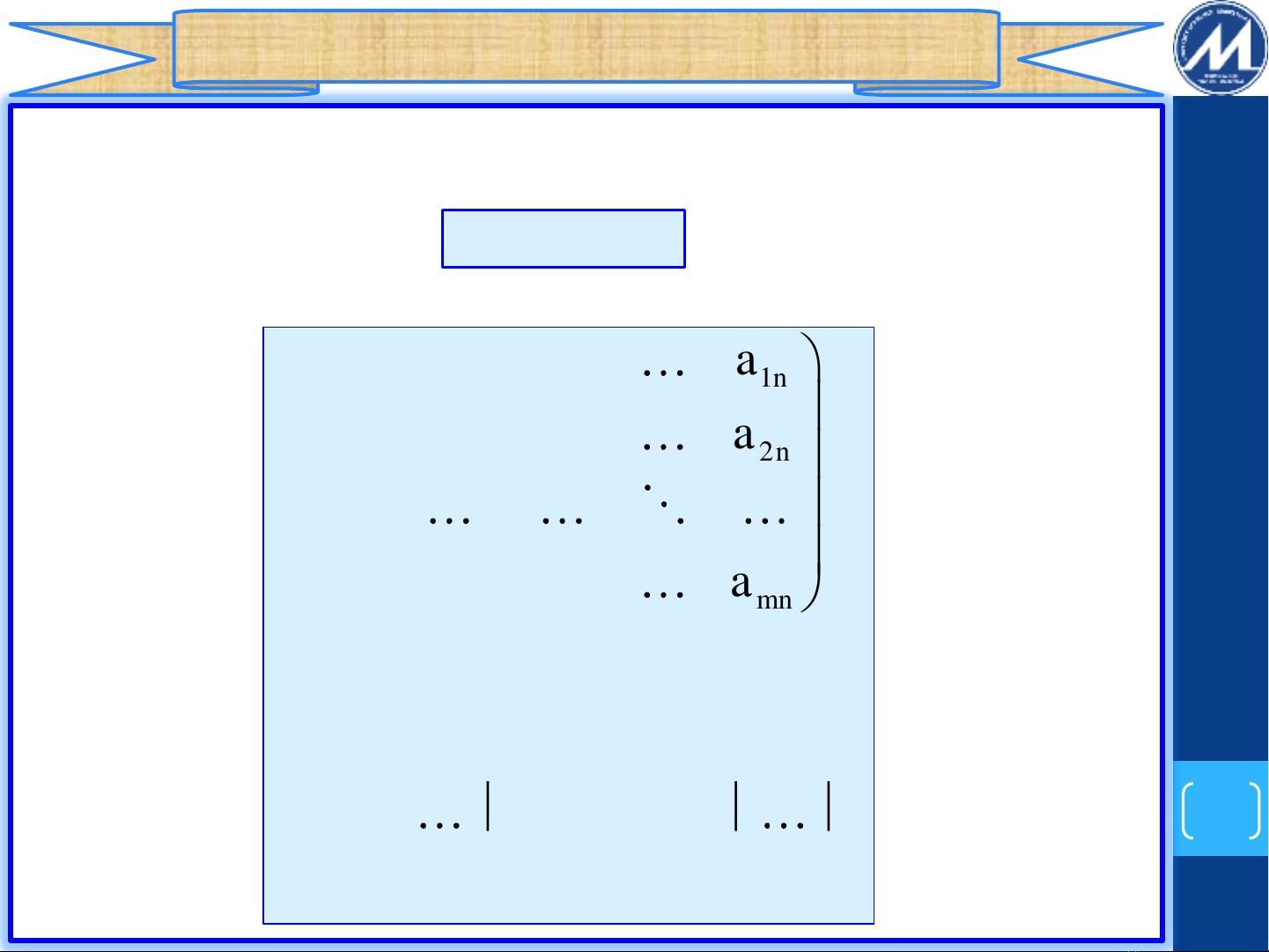
sử dụng các phép biến đổi sơ cấp để đưa ma trận
thành ma trận bậc thang trong đó:
Toán Cao Cấp - ThS. Lê Trường Giang
5
i
b 0, i 1,m
mn
A