HỌC PHẦN TOÁN CAO CẤP 1
CHƯƠNG 6
ỨNG DỤNG PHÉP TÍNH VI PHÂN
QUY TẮC LOPITAN
Giảng viên: Th.S Trịnh Thị Hường
Bộ môn : Toán kinh tế
1. QUY TẮC LÔPITAN
Định lý: Xét giới hạn
lim
𝑥⟶𝑥0
𝑓 𝑥
𝑔(𝑥) 0
0 ∞
∞
Nếu tồn tại giới hạn
lim
𝑥⟶𝑥0
𝑓′ 𝑥
𝑔′(𝑥)
là một số hữu hạn. Khi đó
lim
𝑥⟶𝑥0
𝑓 𝑥
𝑔(𝑥)= lim
𝑥⟶𝑥0
𝑓′ 𝑥
𝑔′(𝑥)
Ví dụ: Tính giới hạn sau
a. lim𝑥→0tan 𝑥−sin 𝑥
𝑥3
b. lim𝑥→∞ ln(𝑥2+2𝑥+3)
ln(𝑥2+5𝑥+7)
CHÚ Ý:
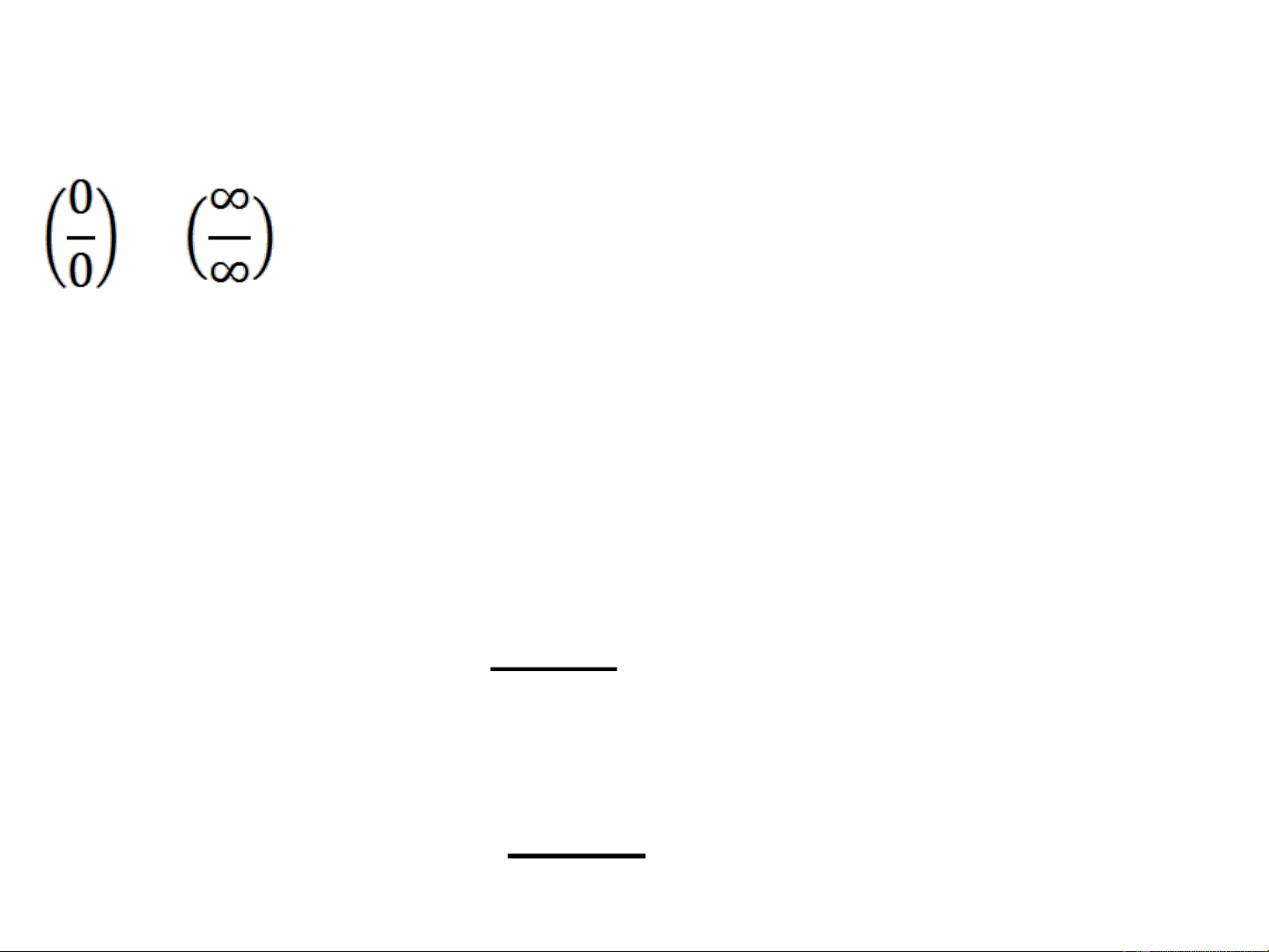
a. Quy tắc lopitan chỉ áp dụng cho giới hạn dạng
. Các dạng vô định khác phải đưa về hai dạng
vô định trên
b. Quy tắc lôpitan có thể được áp dụng liên tiếp nhiều lần
c. Trong một số bài nên kết hợp thay thế VCB để đạo hàm
được đơn giản
d. Nếu giới hạn không tồn tại thì ta phải sử
dụng phương pháp khác để tính
lim
𝑥⟶𝑥0
𝑓′ 𝑥
𝑔′(𝑥)
Ví dụ: lim𝑥→∞ x+sin x
𝑥
2. Dạng vô định
Phương pháp: Quy đồng mẫu số
Ví dụ: Tính giới hạn sau
∞−∞
lim
𝑥→1(𝑥
𝑥 −1−1
ln𝑥)
