Toán cao cấp 2 - Phần Giải tích
Bài 1. Hàm một biến số
Nguyễn Phương
Đại học Ngân hàng TPHCM
Email: nguyenphuong0122@gmail.com
Ngày 3 tháng 12 năm 2024
1
NỘI DUNG
1CÁC KHÁI NIỆM CƠ BẢN VỀ HÀM SỐ 3
2GIỚI HẠN CỦA HÀM SỐ 11
3HÀM SỐ LIÊN TỤC 30
4ĐẠO HÀM CỦA HÀM SỐ 36
5ĐẠO HÀM CẤP CAO 50
6VI PHÂN CỦA HÀM SỐ 52
7ỨNG DỤNG CỦA ĐẠO HÀM 59
Tìm giới hạn của hàm có dang vô định 59
Công thức Taylor - Maclaurin 64
Sự biến thiên của hàm số 74
Cực trị của hàm số 75
8ỨNG DỤNG TRONG KINH TẾ 83
Giá trị biên tế (Marginal quantity) 83
Độ co dãn (Elasticity) 89
Tối ưu trong kinh tế 92
2
CÁC KHÁI NIỆM CƠ BẢN VỀ HÀM SỐ
Từ hàm thường được sử dụng khi đàm luận về tác động liên đới, như được
thấy trong các câu phản hồi sau đây khi tìm kiếm trên Google cụm từ "là
hàm của":
"Hiểu biết là một hàm của kinh nghiệm."
"Dân số loài người là một hàm của lượng cung thực phẩm."
"Tự do là một hàm của trạng thái kinh tế của một quốc gia."
Điểm chung của các phát biểu trên là một đại lượng hay đặc tính nào đó
(hiểu biết, dân số, tự do) phụ thuộc vào một đại lượng khác (kinh nghiệm,
lượng cung thực phẩm, trạng thái kinh tế của một quốc gia). Đây chính là
bản chất của khái niệm hàm trong toán học.
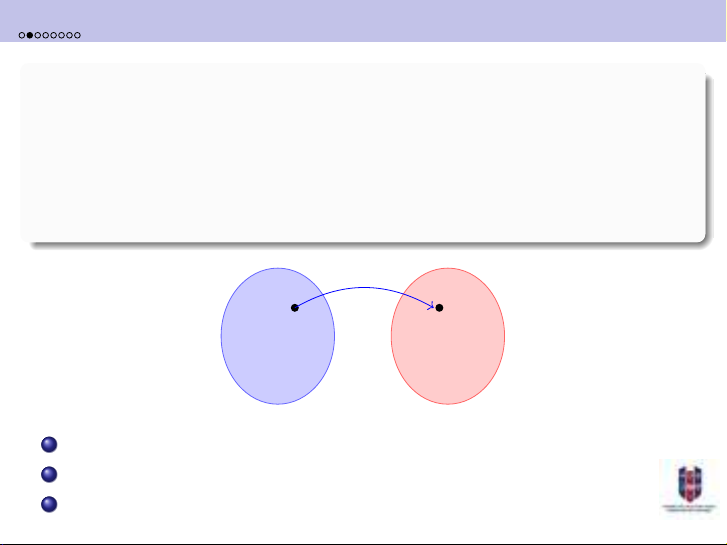
Nói một cách đơn giản, một hàm gồm có hai tập hợp và một quy tắc liên kết
các phần tử của tập hợp này với các phần tử của tập hợp kia.
3
CÁC KHÁI NIỆM CƠ BẢN VỀ HÀM SỐ
Định nghĩa 1.1. Một ánh xạ ftừ một tập hợp Xvào một tập hợp Y(ký hiệu
f:X→Y) là một phép tương ứng liên kết với mỗi phần tử x∈Xvới một
phần tử duy nhất y∈Y, phần tử yđược gọi là ảnh của phần tử x, ký hiệu
y=f(x).
f:X→Y
x7→ y=f(x)
xf(x)
f
1Xđược gọi là tập hợp nguồn.
2Yđược gọi là tập hợp đích.
3yđược gọi là ảnh của xqua f.
4
CÁC KHÁI NIỆM CƠ BẢN VỀ HÀM SỐ
5