Ph n IVầ
H th c đ quyệ ứ ệ
Biên so n:ạ
TS.Nguy n Vi t Đôngễ ế
1
Tài li u tham kh oệ ả
[1] TS. Tr n Ng c H i, Toán r i r cầ ọ ộ ờ ạ
[2] GS.TS. Nguy n H u Anh, Toán r i r c, ễ ữ ờ ạ
Nhà xu t b n giáo d c.ấ ả ụ
[3] Nguy n Vi t H ng’s Slidesễ ế ư
2
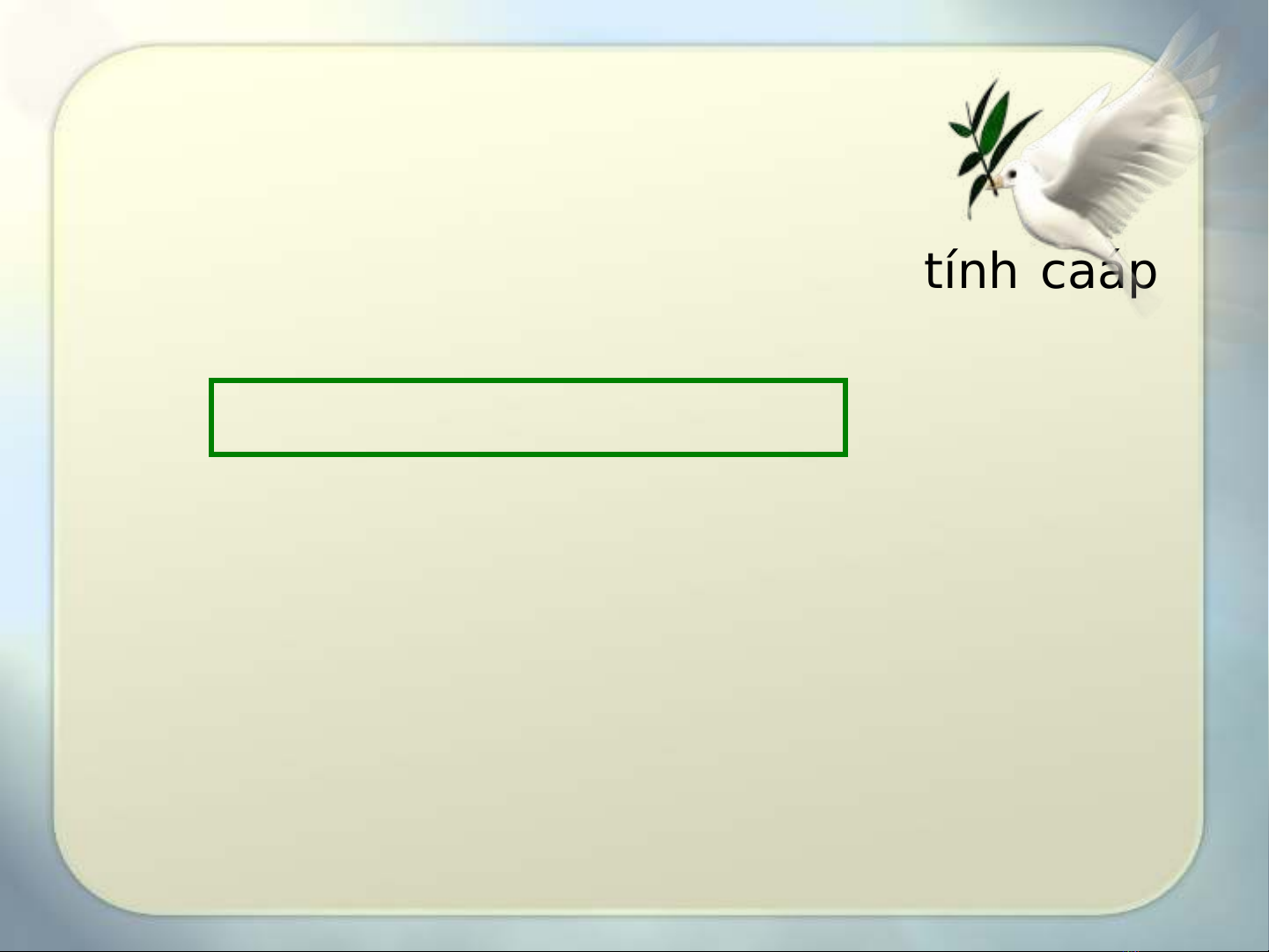
Đnh nghĩaị
Moät heä thöùc ñeä qui tuyeán tính caáp
k laø moät
heä thöùc coù daïng:
xn = a1xn-1 +… + akxn-k + fn (1)
trong ñoù :
• ak 0, a1,…, ak-1 laø caùc heä soá
thöïc
•{fn} laø moät daõy soá thöïc cho
tröôùc
{xn} laø daõy aån nhaän caùc giaù trò
3
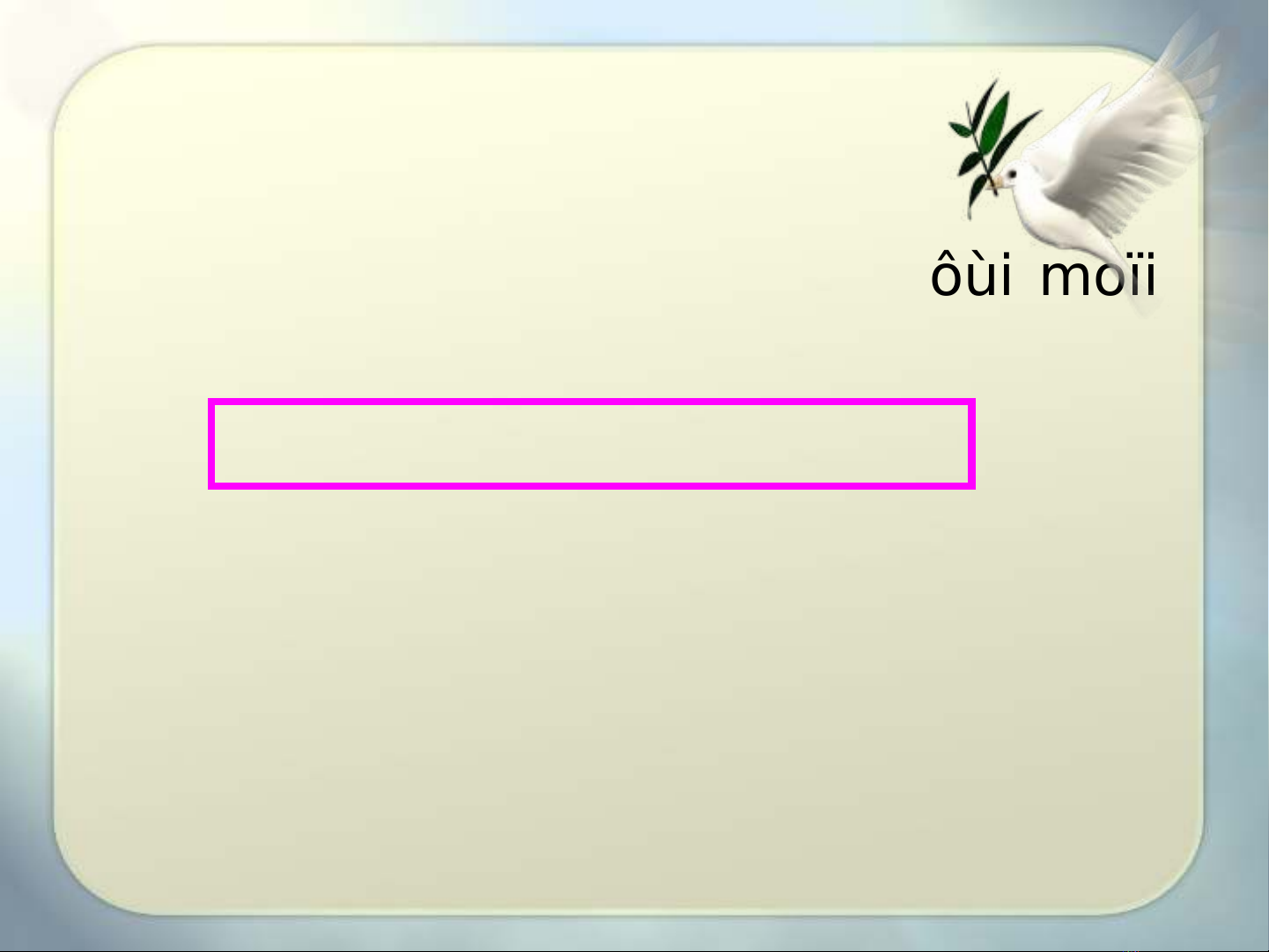
Đnh nghĩaị
Tröôøng hôïp daõy fn= 0 vôùi moïi
n thì (1) trôû
thaønh:
xn = a1xn-1 +… +akxn-k (2)
Ta noùi (2) laø moät heä thöùc ñeä
qui tuyeán tính
thuaàn nhaát caáp k
4
Nghi m t ng quátệ ổ
ØMoãi daõy {xn} thoûa (1) ñöôïc
goïi laø moät nghieäm cuûa (1).
•Nhaän xeùt raèng moãi nghieäm
{xn} cuûa (1) ñöôïc hoaøn toaøn
xaùc ñònh bôûi k giaù trò ban ñaàu
x0, x1,…, xk-1.
ØHoï daõy soá { xn = xn(C1, C2,
…,Ck)} phuï thuoäc vaøo k hoï
tham soá C1, C2,…,Ck ñöôïc goïi
laø nghieäm toång quaùt cuûa (1)
neáu moïi daõy cuûa hoï naøy
ñeàu laø nghieäm cuûa (1)
5