Chương 4
Bài toán cây khung nhỏ nhất
The Minimum Spanning Tree Problem
2
Nội dung
4.1. Cây và các tính ch t c b n c a câyấ ơ ả ủ
4.1. Cây và các tính ch t c b n c a câyấ ơ ả ủ
4.2. Cây khung c a đ thủ ồ ị
4.3. Xây d ng t p các chu trình c b n c a đ thự ậ ơ ả ủ ồ ị
4.4. Bài toán cây khung nh nh tỏ ấ
3
Cây và rừng (Tree and Forest)
§Þnh nghÜa 1. Ta gäi c©y lµ ®å thÞ v« h-íng liªn
th«ng kh«ng c ã chu tr×nh. §å thÞ kh«ng c ã chu
tr×nh ®-îc gäi lµ rõng.
Nh- vËy, rõng lµ ®å thÞ mµ mçi thµnh phÇn liªn
th«ng c ña nã lµ mét c©y.
T1T3
Rừng F gồm 3 cây T1, T2,, T3
T2
4
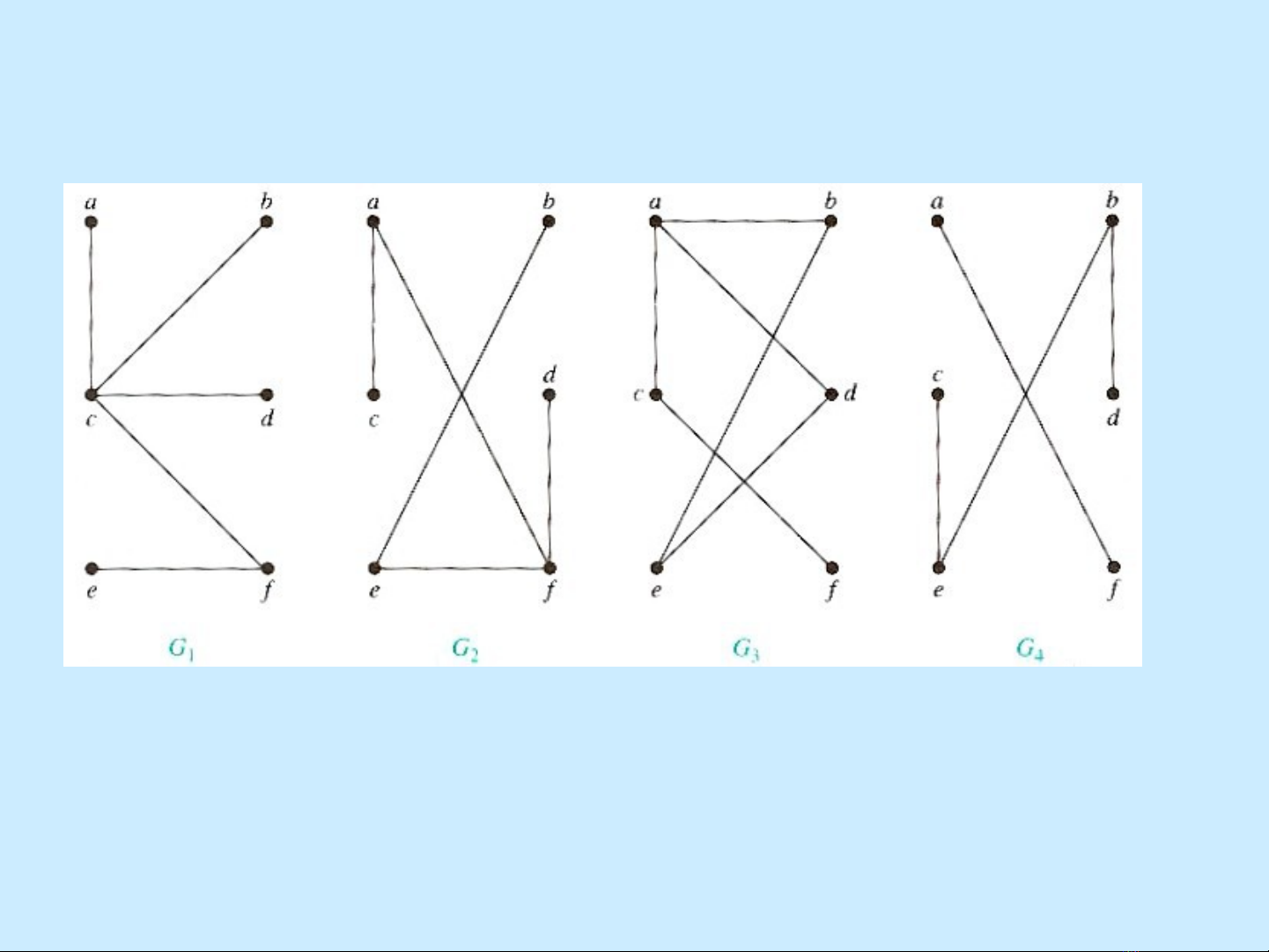
VÍ DỤ
G1, G2 là cây
G3, G4 không là cây
5
Các tính chất cơ bản của cây
Đnh lý 1. ịGi s T=ả ử (V,E) là đ th vô h ng n đnh. ồ ị ướ ỉ
Khi đó các m nh đ sau đây là t ng đng:ệ ề ươ ươ
(1) T là liên thông và không ch a chu trình;ứ
(2) T không ch a chu trình và có n-1 c nh;ứ ạ
(3) T liên thông và có n-1 c nh;ạ
(4) T liên thông và m i c nh c a nó đu là c u;ỗ ạ ủ ề ầ
(5) Hai đnh b t k c a T đc n i v i nhau b i ỉ ấ ỳ ủ ượ ố ớ ở
đúng m t đng đi đn;ộ ườ ơ
(6) T không ch a chu trình nh ng h c thêm vào ứ ư ễ ứ
nó m t c nh ta thu đc đúng m t chu trình.ộ ạ ượ ộ