Bài giảng Vật lí hiện đại: Chương 2 - Huỳnh Nguyễn Phong Thu

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:28

Thêm vào BST

Báo xấu

18
lượt xem 4
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Vật lí hiện đại - Chương 2 Cơ sở của cơ học lượng tử, cung cấp cho người học những kiến thức như: Giả thuyết De Broglie; thí nghiệm kiểm chứng; hệ thức bất định Heisenberg; hàm sóng và ý nghĩa xác suất; điều kiện chuẩn hóa và nguyên lý chồng chất trạng thái;...Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Vật lí hiện đại: Chương 2 - Huỳnh Nguyễn Phong Thu

VẬT LÝ HIỆN ĐẠI CHƯƠNG 2: CƠ SỞ CỦA CƠ HỌC LƯỢNG TỬ GV: Huỳnh Nguyễn Phong Thu Email: hnpthu@hcmus.edu.vn SĐT: 0903122520 1
GIẢ THUYẾT DE BROGLIE Ánh sáng có lưỡng tính sóng – hạt. Vật chất thì sao?? Giả thuyết De Broglie: Vật chất thông thường cũng có lưỡng tính sóng – hạt như ánh sáng. Louis De Broglie Ø Sóng này gọi là sóng vật chất hay sóng De Broglie. Ø Hạt có xung lượng: = l là bước sóng De Broglie p đại diện cho tính chất hạt, l đại diện cho tính sóng của vật chất 2
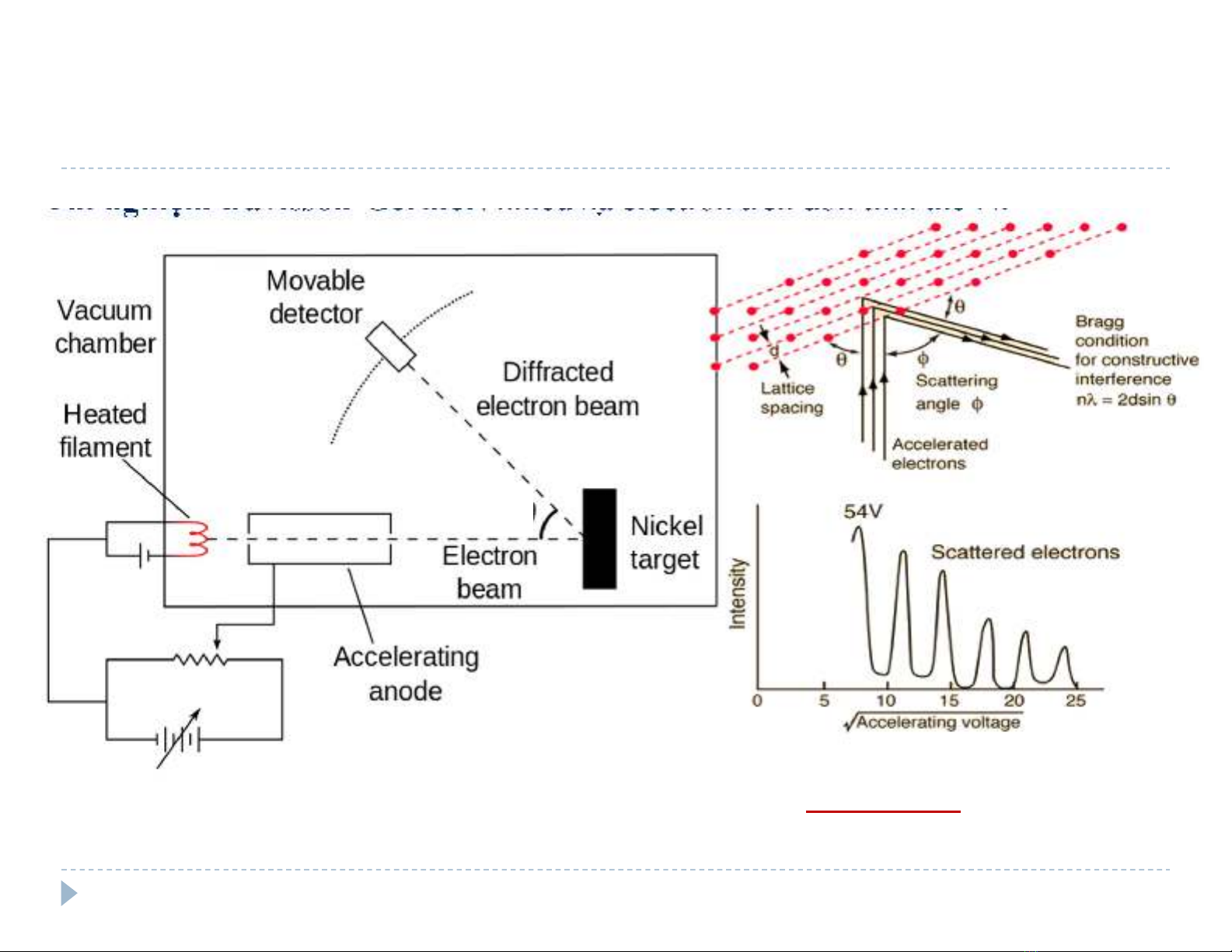
THÍ NGHIỆM KIỂM CHỨNG Thí nghiệm Davisson-Germer: nhiễu xạ electron trên đơn tinh thể Ni ϕ − Cực đại nhiễu xa:̣ . = = 3
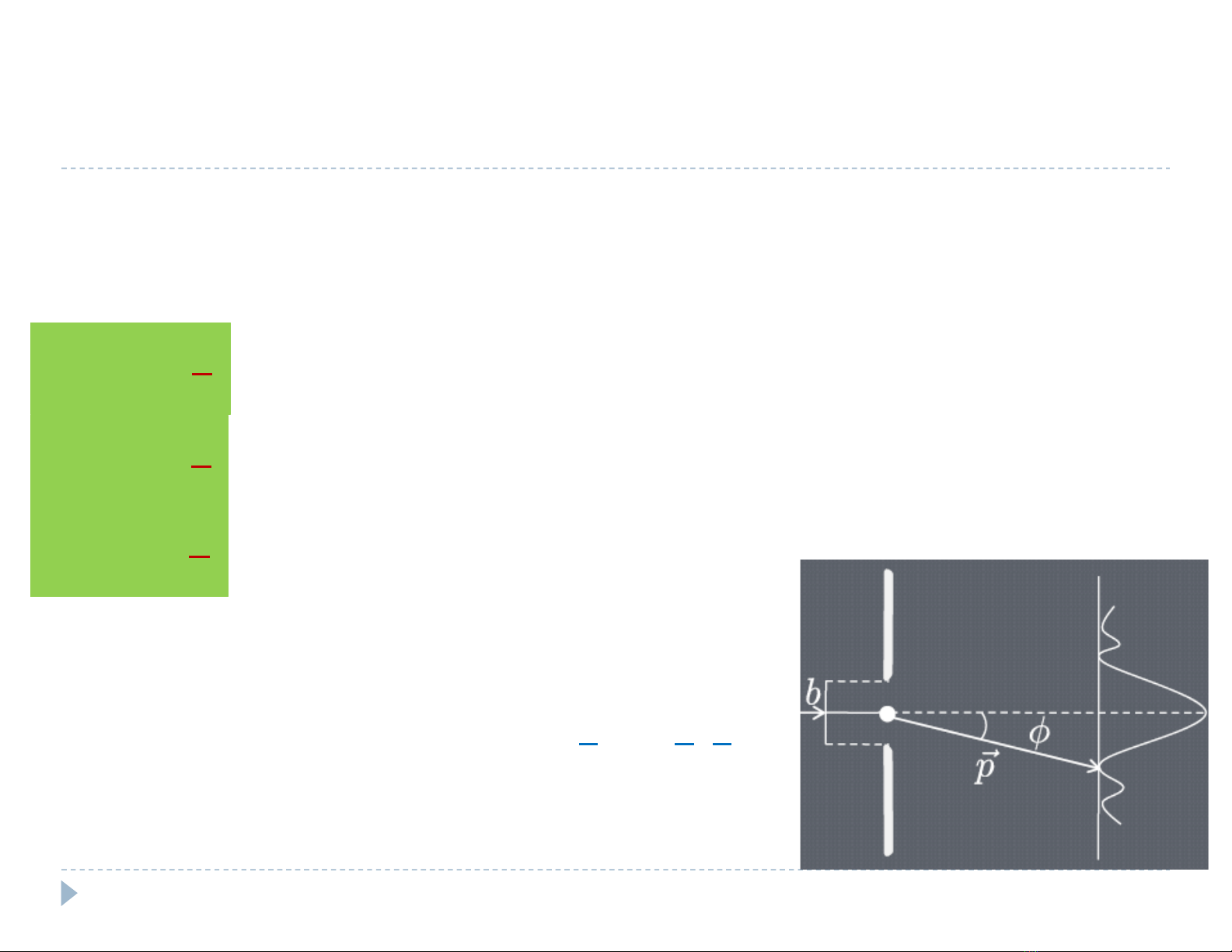
HỆ THỨC BẤT ĐỊNH HEISENBERG Không thể xác định được tọa độ và xung lượng tương ứng của một hạt đồng thời với độ chính xác tùy ý. ℏ Xét hiện tượng nhiễu xạ qua một khe hẹp của chùm vi hạt: ≥ Ø Vị trí của hạt: ℏ ≥ 0≤ ≤ ⇒ ≈ ℏ Ø Hình chiếu của động lượng theo phương x: ≥ 0≤ ≤ sin ⇒ ≈ sin Ø Điều kiện cực tiểu nhiễu xạ: ℎ sin = ⁄ ⇒ . ≈ . . = . . =ℎ 4
HỆ THỨC BẤT ĐỊNH HEISENBERG Năng lượng của hệ ở trạng thái nào càng bất định thì thời gian để hệ tồn tại ở trạng thái đó càng ngắn (xác định) và ngược lại. ℏ ≥ Trạng thái bền của một hệ là trạng thái mà hệ vẫn tồn tại ở trạng thái đó trong một khoảng thời gian dài. Ngược lại là trạng thái không bền. è Trạng thái có năng lượng xác định là trạng thái bền, trạng thái có năng lượng bất định là trạng thái không bền Hệ thức bất định chỉ áp dụng cho thế giới vi mô Vị trí hạt không thể xác định được một cách chính xác mà luôn có 1 xác suất xuất hiện Quy luật chuyển động tuân theo quy luật thống kê 5
HÀM SÓNG VÀ Ý NGHĨA XÁC SUẤT Sóng ánh sáng: ~| | = , , , Xác suất xuất hiện electron ~cường độ ánh sáng è xác suất có electron cũng là bình phương của một đại lượng y(x, y, z, t) nào đó. y làm một hàm sóng phức. Xác suất xuất hiện electron: | , , , | Sóng vật chất De Broglie là sóng xác suất và cũng tuân theo các quy luật như sóng ánh sáng Xác suất tìm thấy hạt trong thể tích dV=dxdydz bao quanh điển (x,y,z) tại thời điểm t: | , , , | | , , , | Được gọi là mật độ xác suất của hạt tại (x,y,z) 6
ĐIỀU KIỆN CHUẨN HÓA VÀ NGUYÊN LÝ CHỒNG CHẤT TRẠNG THÁI Xác suất để tìm thấy hạt ở mọi nơi (điều | , , , | = kiện chuẩn hóa của hàm sóng) Mỗi electron có một sóng xác suất è sóng tán xạ và tách ra nhiều sóng yi Tại một điểm các sóng này chồng chất lên nhau Tăng cường Xác suất lớn = + +. . . Triệt tiêu Xác suất bé Một hệ có thể ở trạng thái y1, y2,.. Thì cũng có thể ở trong trạng thái = + +. . . Xác suất tìm thấy hệ ở trạng thái yi tỷ lệ với bình phương trị tuyệt đối của hệ số tương ứng | | 7
HÀM SÓNG CỦA HẠT TỰ DO Hàm sóng của sóng De Broglie tương tự như phương trình sóng phẳng: = os − = os2 − (1) 1 ℎ ℎ 1 = = , = ⇒ = os − (1’) ℏ 1 Xét sóng truyền trong không gian 3 chiều: = os − ⃗⃗ ℏ Viết dạng phức: = ℏ = ℏ ℏ (2) 8
PHƯƠNG TRÌNH SCHRODINGER PHỤ THUỘC THỜI GIAN Hàm sóng De Broglie của hạt tự do: (4) , , , = ℏ ℏ =− = = = ℏ ℏ ℏ ℏ =− =− =− ℏ ℏ ℏ ⇒ + + =− (5) ℏ = + + 9
PHƯƠNG TRÌNH SCHRODINGER PHỤ THUỘC THỜI GIAN Năng lượng toàn phần của hạt: = + = + (6) 2 Nhân hàm sóng y: = + (7) 2 = ℏ = −ℏ + + ℏ ℏ ℏ =− + + + =− + (8) 2 2 è Đây là phương trình Schrodinger tổng quát 10
PHƯƠNG TRÌNH SCHRODINGER Ở TRẠNG THÁI DỪNG Hàm sóng có thể phân li biến số theo không gian và thời gian: , , , = ℏ , , (9) Phương trình Schorodnger tổng quát được viết lại: ℏ , , ℏ =− , , ℏ + , , ℏ (10) 2 2 (11) , , + − , , =0 ℏ è Đây là phương trình Schrodinger ở trạng thái dừng 11
HẠT TRONG HỐ THẾ MỘT CHIỀU U(x) ∞ khi x ≤ 0 U x = 0 khi 0
HẠT TRONG HỐ THẾ MỘT CHIỀU ψ 0 = Asin k. 0 + Bcos k. 0 = 0 ⇒ B = 0 ⇒ ψ x = Asin kx πn ψ a = Asin ka = 0 ⇒ k = a nπx |ψ x | dx = 1 ⇔ A sin dx = 1 a 2 ⇔A − =1 ⇒A= a 2 nπx ψ x = sin a a 13
HẠT TRONG HỐ THẾ MỘT CHIỀU 2mE πn π ℏ k = k= E = n ℏ a 2ma Năng lượng của hạt bị lượng tử hóa. Hạt chỉ có thể có những mức năng lượng xác định chứ không thể có mọi năng lượng tùy ý π ℏ Năng lượng của hạt ở TTCB: E = 2ma Mật độ xác suất tìm thấy hạt trong hố thế: 2 nπx |ψ x | = sin a a 14
RÀO THẾ – HIỆU ỨNG ĐƯỜNG NGẦM U(x) 0 khi x ≤ 0 U x = U0 khi 0
RÀO THẾ – HIỆU ỨNG ĐƯỜNG NGẦM Nghiệm các phương trình vi phân: ψ =A e +B e ψ =A e +B e ψ =A e +B e A3e Đặc trưng cho sóng truyền qua rào thế B3e Mô tả sóng phản xạ từ vô cực trở về 16
RÀO THẾ – HIỆU ỨNG ĐƯỜNG NGẦM Hệ số truyền qua rào là tỷ số giữa bình phương biên độ sóng truyền qua hàng rào và sóng tới, tương tự đối với hệ số phản xạ |A | A D= =| | |A | A |B | B R= =| | |A | A Điều kiện bảo toàn số hạt |A | = |B | + |A | D+R=1 17
RÀO THẾ – HIỆU ỨNG ĐƯỜNG NGẦM Áp dụng các điều kiện biên (tại x=0 và x=a) Ta được các hệ thức: ψ 0 =ψ 0 dψ dψ A +B =A +B | = | ik A − B = −k A − B dx dx ψ a =ψ a A e +B e =A dψ dψ | = | −k A e −B e = ik A dx dx 18
RÀO THẾ – HIỆU ỨNG ĐƯỜNG NGẦM 1 − in 1 + in k E A = A e B = A e n= = 2 2 k U −E n+i n+i 1 − in A = A = A e 2n 2n 2 16n D= e 1+n ≈ ℏ Khi E
BÀI TẬP Bài 1: Tìm bước sóng De Broglie của (a) một quả golf khối lượng 46g bay với vận tốc 30m/s, (b) một electron có vận tốc 107 m/s. Bài 2: Tìm động năng của proton có bước sóng 10-15m. Biết proton có năng lượng nghỉ E0=938MeV. Bài 3: Một electron có bước sóng 2.10-12m. Tìm động năng và vận tốc của nó, biết năng lượng nghỉ của electron E0=511keV. Bài 4: Tính bước sóng của electron sau khi nó được gia tốc qua hiệu điện thế 25kV. Bài 5: Bằng việc thực hiện phép đo thực nghiệm về nhiễu xạ hạt nhân, bạn đo bước sóng De Broglie của proton là 9,16.10-15m. a. Tính vận tốc của proton b. Để đạt vận tốc này thì hiệu điện thế cần gia tốc cho proton bằng bao nhiêu? Bài 6: Một con báo có thể chạy với vận tốc 28m/s. Nếu con báo có bước sóng De Broglie 8,97.10-37m thì con báo có khôi lượng bao nhiêu. Bài 7: Tính bước sóng của proton trong tia vũ trụ nếu nó chuyển động với động năng a) 2GeV, b) 200 GeV. Biết năng lượng nghỉ của proton là 938MeV. 20