BÀI T P L N MÔN TH Y L C CÔNG TRÌNHẬ Ớ Ủ Ự
N03
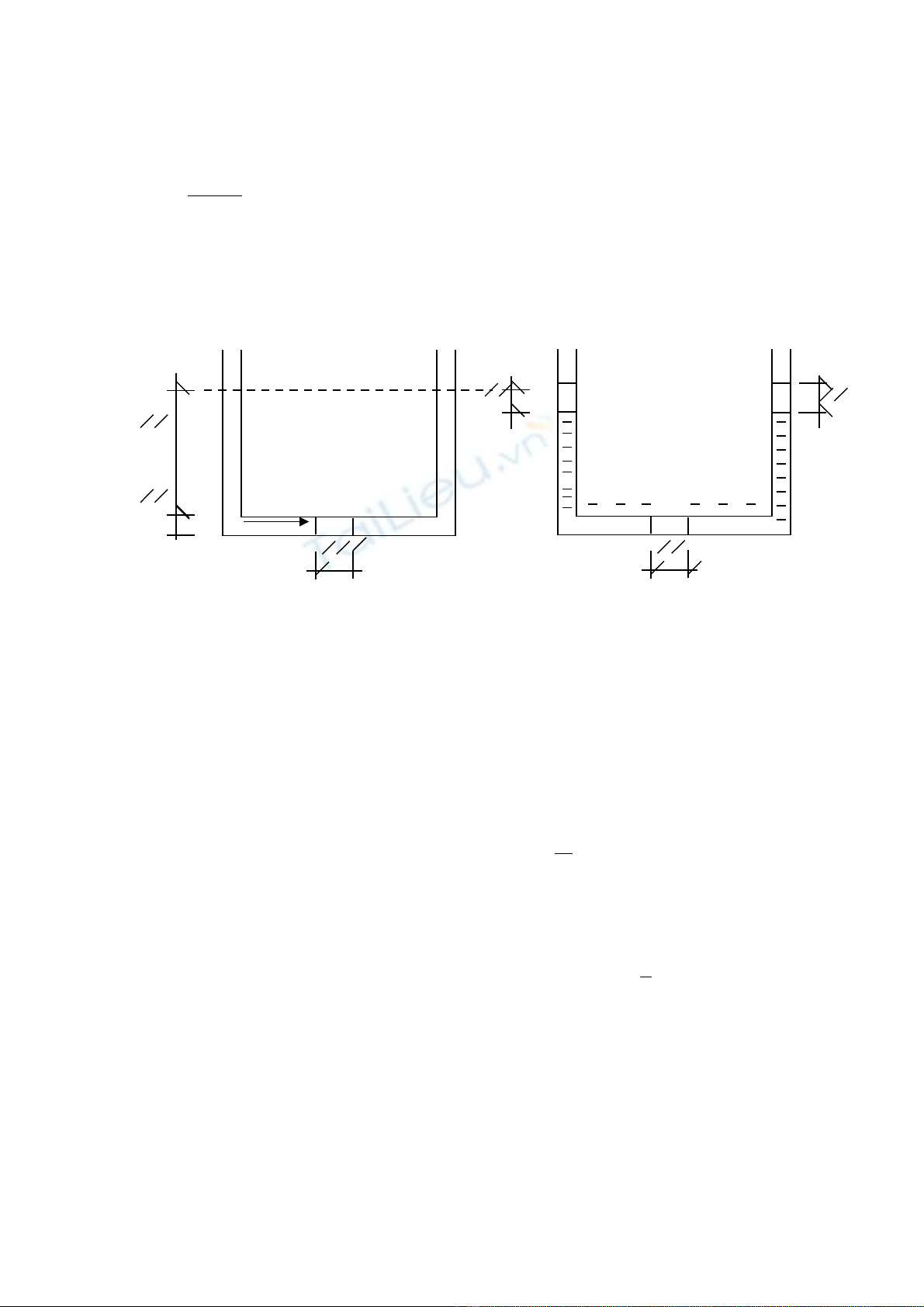
Bài 3 : M t ng ti p bên trong có m t píttông có th tr t không ma sát.ộ ố ế ộ ể ượ
Ti t di n c a píttông và c a ng là S. ng đ c u ng thành hình ch U vàế ệ ủ ủ ố Ố ượ ố ữ
đ ng n c. hai nhánh có cùng đ cao.ự ướ Ở ộ
Tính công đ y píttôngdi chuy n m t đo n l.ẩ ể ộ ạ
Cho l=0,1m; S=0.05m2 (A=γl2S đáp s )ố
Gi iả
Gi s pittông di chuy n t trái sang ph i m t đo n l. do ng ti p cóả ử ể ừ ả ộ ạ ố ế
cùng m t ti t di n nên khi đ y chuy n 1 đo n l thì m t ch t l ng nhánh Bộ ế ệ ẩ ể ạ ặ ấ ỏ ở
tăng lên 1 đo n l.ạ
⇒ Công đ y pittông di chuy n b ng công nâng m t kh i ch t l ng lênẩ ể ằ ộ ố ấ ỏ
đo n l.ạ
A=(γ*S*l)l==γ*S*l2
Khi n c 2 nhánh có cùng đ cao thì áp l c d c a n c tác d ngướ ở ộ ự ư ủ ướ ụ
vào pittông b ng nhau: nhánh A và nhánh B.ằ
S
h
hNN A
d
B
d*)
2
(2
1+==
γ
Khi pittông d ch chuy n m t đo n l thì n c nhánh B dâng lên m tị ể ộ ạ ướ ở ộ
đo n l và n c nhánh A h xu ng m t đo n l, thì l c tác d ng vào pittôngạ ướ ở ạ ố ộ ạ ự ụ
s b ng đ chênh l ch áp l c d nhánh tác d ng vào pittông.ẽ ằ ộ ệ ự ư ở ụ
)( '' FNhayNNNF A
d
A
d
B
d
B
d=−−=
=
SlS
h
hShlh ***)
2
(*)( 121
γγγ
=+−++
V y công đ y pittông di chuy n m t đo n l.ậ ẩ ể ộ ạ
⇒ A=F*l=
SllSl ***)**( 2
γγ
=
l
h1
h2
l
l
l
N03
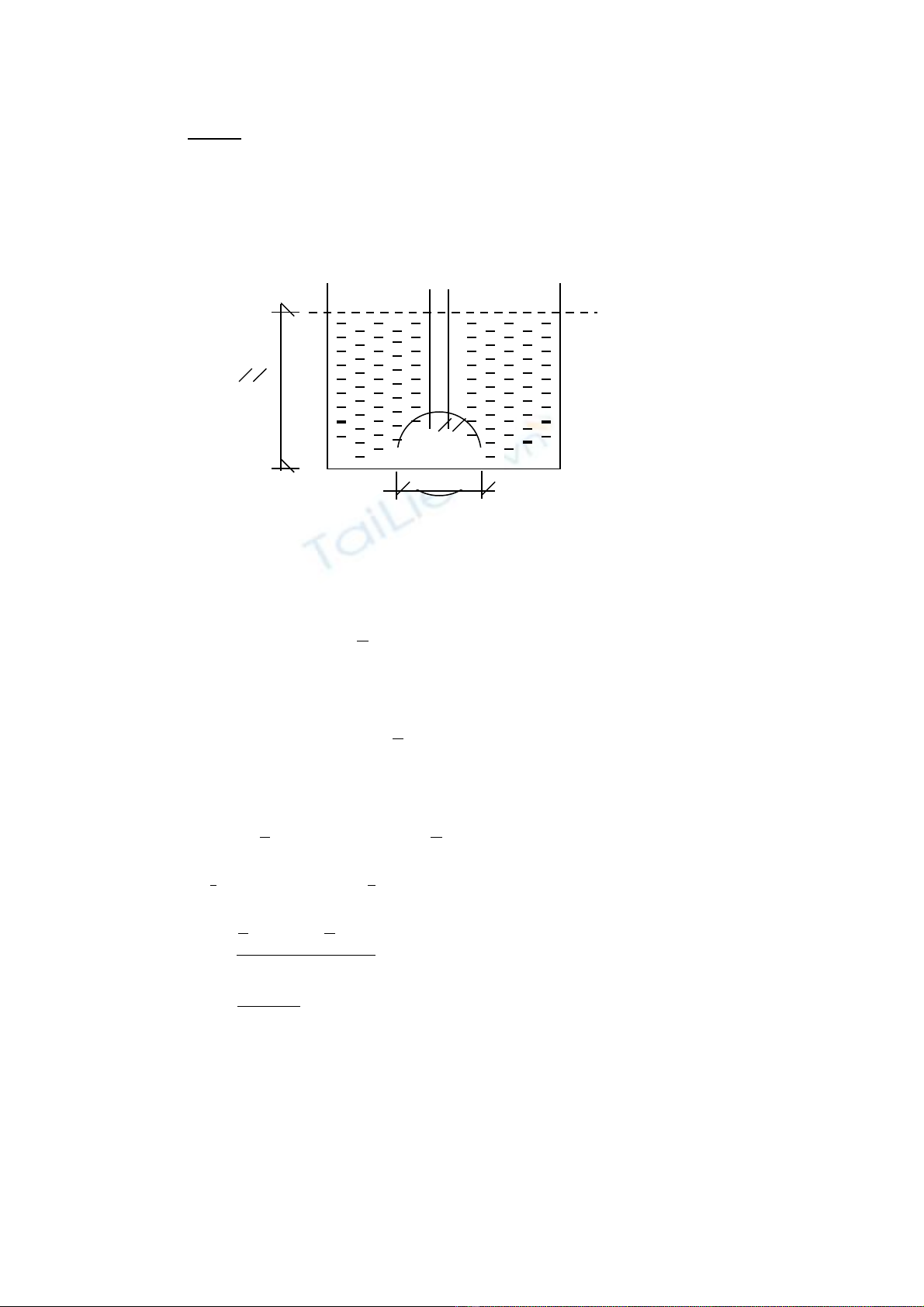
Bài 4 : M t ph u hình bán c u úp ng c vào đáy m t thùng và đ c rótộ ể ầ ượ ộ ượ
đ y th y ngân đ n đ nh bán c u. Đ gi ph u n m yên ng i ta đ n c vàoầ ủ ế ỉ ầ ể ữ ể ằ ườ ổ ướ
thùng. Tính chi u cao t i thi u c a n c đ ph u n m cân b ng. B qua thề ố ể ủ ướ ể ể ằ ằ ỏ ể
tích cu n ph u và tr ng l ng ph u. Gi thi t cu n ph u đ cao đ luônố ể ọ ượ ể ả ế ố ể ủ ể
luôn nhô lên trên m t n c.ặ ướ
Đ ph u n m cân b ng thì áp l c c a th y ngân và áp l c c a n c tácể ể ằ ằ ự ủ ủ ự ủ ướ
d ng lên ph u ph i b ng nhau.ụ ể ả ằ
Áp l c c a th y ngân.ự ủ ủ
Nd=γHg-
)*
3
2
**( 32 RRR
ππ
−
(1)
Áp l c c a n c.ự ủ ướ
)*
3
2
**(* 32
2
2RRkN OH
OH
d
ππγ
−=
V y chi u cao t i thi u c a n c đ ph u n m cân b ng.ậ ề ố ể ủ ướ ể ể ằ ằ
T (1) và (2)ừ
⇒
)**
3
2
**()
3
1
(* 323 RRhR
Hg
ππγπγ
−=
⇔
323
**
3
2
*****
3
1RRhR
Hg
πγπγπγ
−=
⇒
πγ
πγπγ
2
33
3
2
3
1
R
RR
h
Hg +
=
⇒
R
Hg
h*
3
2
γ
γ
+
=
h
Hg
2R


























