Bài tp Lý Thuyt Tín Hiu sưu tm bi Trn Văn Thưng
Trang 1
Bài 1.1. Hãy tính tích phân, năng lưng, ñ rng trung bình ca các tín hiu
sau ñây:
a)
(
)
(
)
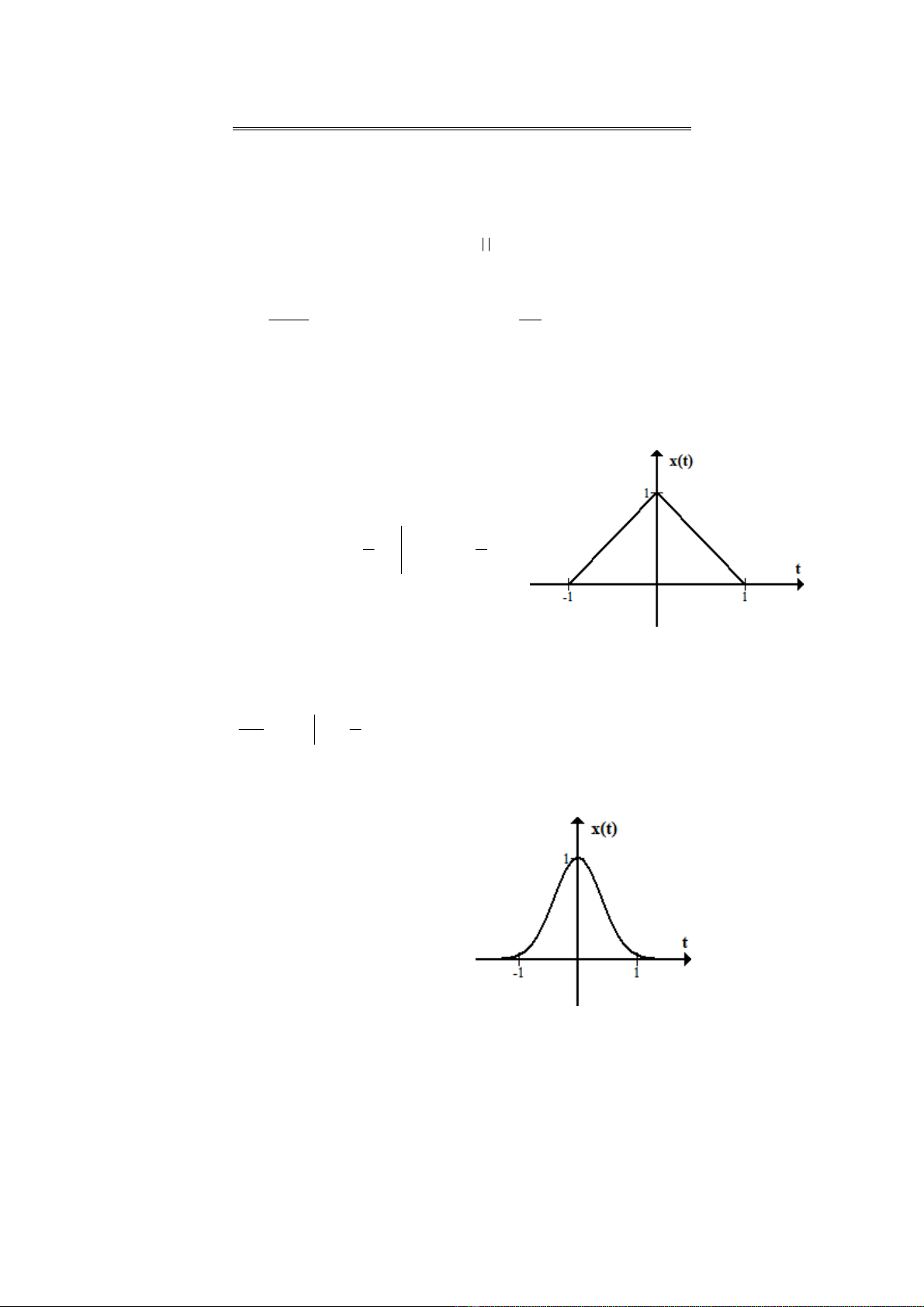
ttx Λ=
d)
(
)
t
tetx
−
=
b)
(
)
2
t
etx
π
−
=
e)
(
)
(
)
(
)
tetetx
tt
11
2−
+−=
c)
( )
2
1
1
t
tx
+
=
f)
( )
Π=
π
3
cos t
ttx
Gii
a)Tích phân ca tín hiu là:
[ ]
( )
∫
∞
∞−
=dttxx
( ) ( )
∫ ∫
−
−++=
0
1
1
0
11 dttdtt
( )
∫
−= 1
012 dtt
1
0
2
2
1
−= tt
−= 2
1
12
1
=
Năng lưng ca tín hiu là:
( )
[ ]
∫∞
∞−
=
dttx
Ex
2
( )
dtt
∫
−=
1
0
2
12
( )
1
0
3
1
3
2
t
−
−
=
3
2
=
b)
(
)
2
t
etx
π
−
=
*Tích phân ca tín hiu là:
[ ]
( )
∫∞
∞−
=
dttxx
(
)
∫∞
∞−
−
=
dte t2
π
ðt
(
)
∫∞
∞−
−
=
dte t2
π
dyedxeI
yx
∫
∫
−−
=⇒
ππ
2
(
)
dxdye
yx
∫∫
+−
=
22
π
ñt
ϕ
cos
r
x
=
và
ϕ
sinry
=
Bài tp Lý Thuyt Tín Hiu sưu tm bi Trn Văn Thưng
Trang 2
∫∫ ∞−
=⇒0
2
0
22rdredI r
π
π
ϕ
∫
∞−
×=
0
2
2
2
1
2dre
r
π
π
2
0
r
e
π
−
=
−
∞
1
=
1
=
⇒
I
*Năng lưng ca tín hiu là:
( )
[ ]
∫
∞
∞−
=dttx
E
x
2
(
)
∫
∞
∞−
−
=dte
t
2
2
π
ðt
M
(
)
∫
∞
∞−
−
=dte
t
2
2
π
dyedxeM
yx
∫
∫
−−
=⇒
22
222
ππ
(
)
dxdye
yx
∫∫
+−
=
22
2
π
ñt
ϕ
cos
r
x
=
và
ϕ
sinry
=
∫∫
∞−
=⇒
0
2
2
0
2
2
rdredM
r
π
π
ϕ
∫
∞−
×=
0
22
2
2
1
2dre
r
π
π
2
2
2
1
0
r
e
π
−
=
−
∞
2
1
=
⇒
( )
[ ]
∫
∞
∞−
=dttx
E
x
2
M
=
2
2
=
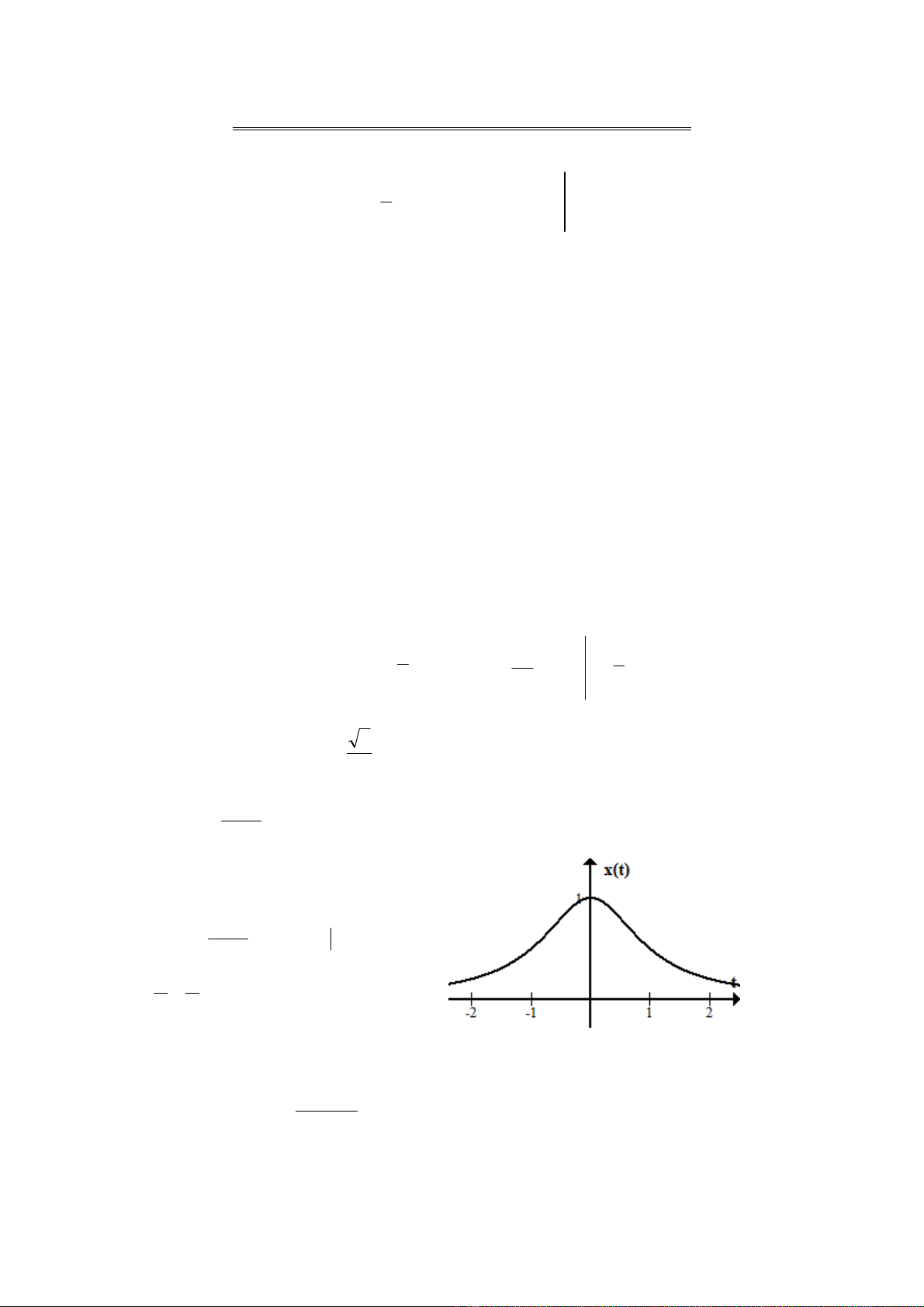
c)
( )
2
1
1
t
tx
+
=
* Tích phân ca tín hiu là:
[ ]
π
ππ
=+=
=
+
=
∞
∞−
∞
∞−
∫
22
1
1
)(
2
acrtgtdt
t
tx
* Năng lưng ca tín hiu là:
( )
[ ]
∫
∞
∞−
=dttx
E
x
2
=
∫
∞
∞−
+dt
t
22
)1(
1
Bài tp Lý Thuyt Tín Hiu sưu tm bi Trn Văn Thưng
Trang 3
ðt
tgu
t
=
( )
( )
2
4
1
22sin
4
1
)12(cos
2
1
cos
cos
1
cos
cos
1
)1(
1
2
2
2
2
2
2
2
2
2
2
4
2
2
222
π
ππ
π
π
π
π
π
π
π
π
π
π
=+=
+=+=
==
+
=⇒
∫
∫∫
∫
−−
−−
−
uuduu
ududu
u
u
du
uutg
E
x
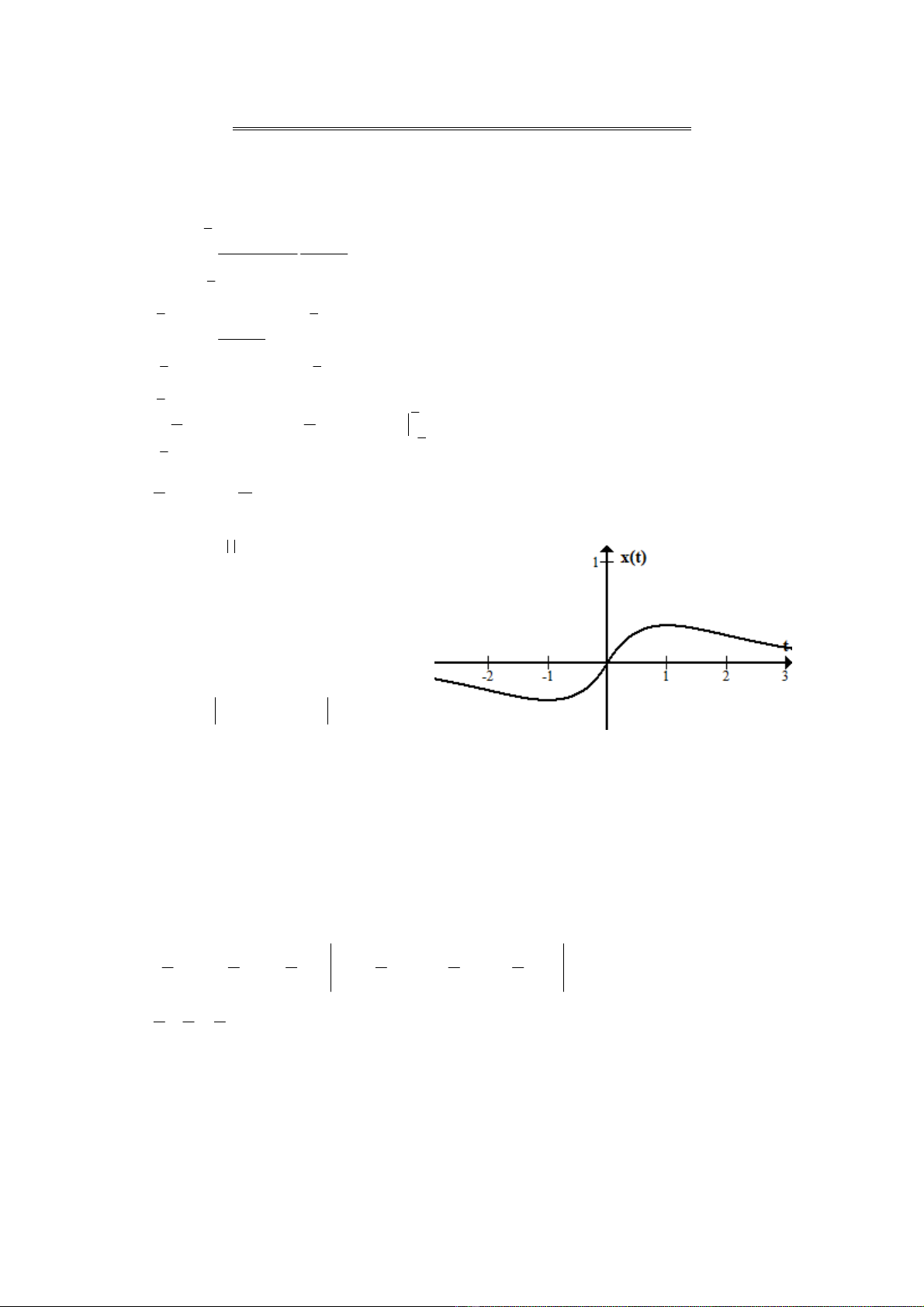
d)
(
)
t
tetx
−
=
* Tích phân ca tín hiu là:
[ ]
( ) ( )
0
1
1
0
0
0
0
=
+
−
=
++−=
+=
∞
−−
∞−
∞−
∞−
∫∫
tttt
tt
eteete
dttedttex
* Năng lưng ca tín hiu là:
( )
[ ]
∫
∞
∞−
=dttx
E
x
2
2
1
4
1
4
1
4
1
2
1
2
1
4
1
2
1
2
1
0
2222
0
2222
0
22
0
22
=+=
++−
+−=
+=
∞
−−−
∞−
∞−
∞−
∫∫
tttttt
tt
eteeteteet
dtetdtet
e)
(
)
(
)
(
)
tetetx
tt
11
2−
+−=
* Tích phân ca tín hiu là:
Bài tp Lý Thuyt Tín Hiu sưu tm bi Trn Văn Thưng
Trang 4
[ ]
2
3
1
2
1
2
1
0
0
2
0
0
2
=+=−=
+=
∞
−
∞−
∞−
∞−
∫∫
tt
tt
ee
dtedtex
* Năng lưng ca tín hiu là:
( )
[ ]
∫∞
∞−
=dttx
Ex
2
4
3
2
1
4
1
2
1
4
1
0
2
0
4
0
2
0
4
=+=−=
+=
∞
−
∞−
∞−
∞−
∫∫
tt
tt
ee
dtedte
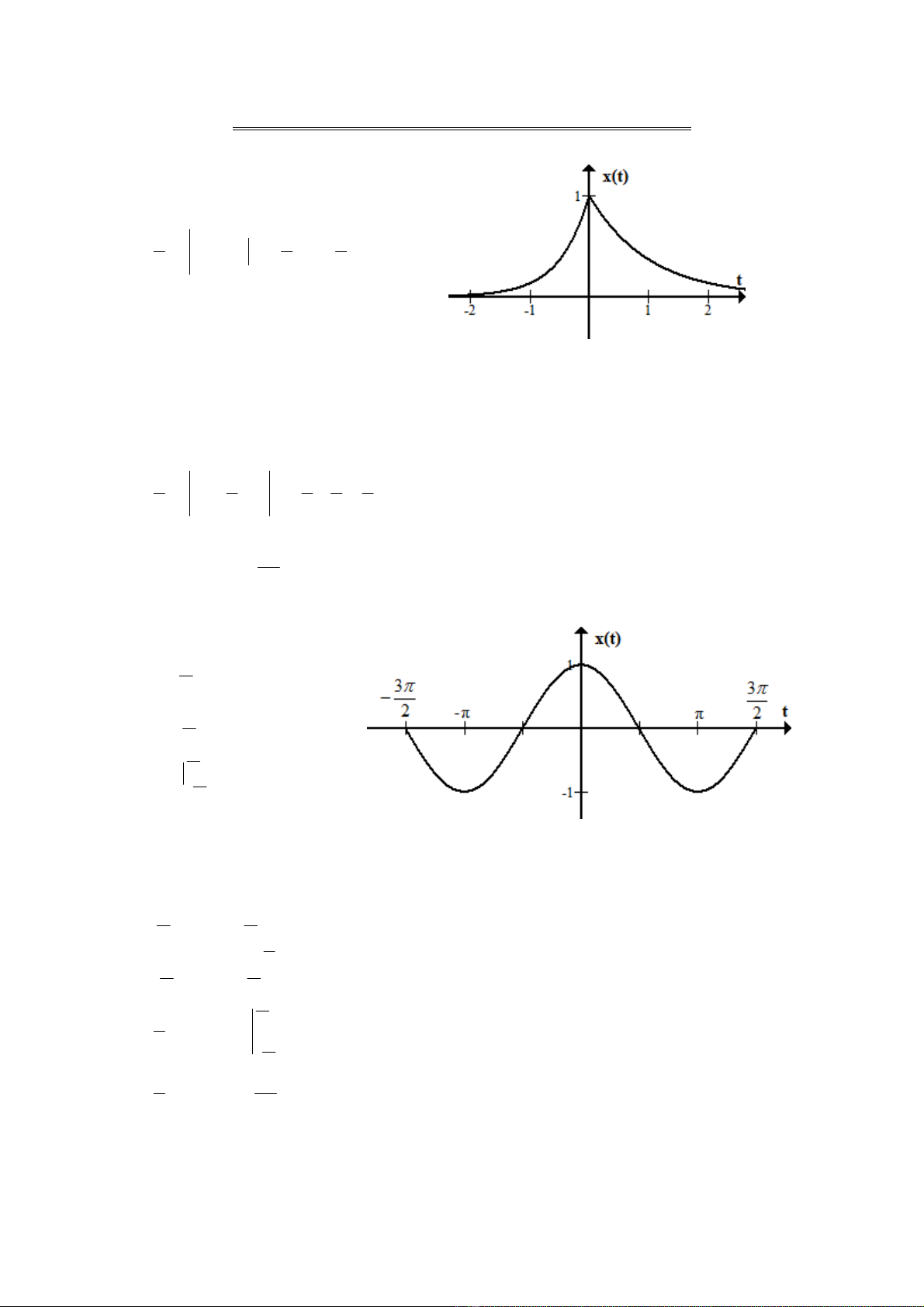
f)
( )
Π=
π
3
cos t
ttx
* Tích phân ca tín hiu là:
[ ]
211sin
cos
2
3
2
3
2
3
2
3
−=−−==
=
−
−
∫
π
π
π
π
t
tdtx
* Năng lưng ca tín hiu là:
( )
[ ]
( )
( )
( )
2
3
33
4
1
2cos2
4
1
2sin1
2
1
cos
2
3
2
3
2
3
2
3
2
3
2
3
2
2
π
ππ
π
π
π
π
π
π
=+=
+=
−==
=
−
−−
∞
∞−
∫∫
∫
tt
dtttdt
dttx
Ex
Bài tp Lý Thuyt Tín Hiu sưu tm bi Trn Văn Thưng
Trang 5
Bài 1.2 Dòng ñin i(t) = Ie
t
β
−
1(t) chy qua ñin tr R .Hãy tìm :
a )Năng lưng tiêu hao trên ñin tr R trong khong t(0;∞)
b )Năng lưng tiêu hao trên ñin tr R trong khong t(0;1/β)
Gii
a)Năng lưng tiêu hao trên ñin tr R trong khong t(0;∞) là:
E =
)()(
2
0
tdtiR
∫
∞
=
)(
2
0
tdIeR
t
∫
∞−
β
=
)(
2
0
2
tdeRI
t
∫
∞−
β
=
∞−
−
0
2
2
2
t
e
RI
β
β
=
)10(
2
2
−
−
β
RI
=
β
2
2
RI
b)Năng lưng tiêu hao trên ñin tr R trong khong t(0;1/β) là :
E =
)()(
2
/1
0
tdtiR
∫
β
=
)(
2
/1
0
tdIeR
t
∫
−
ββ
=
)(
2
/1
0
2
tdeRI
t
∫
−
ββ
=
ββ
β
/1
0
2
2
2
t
e
RI
−
−
=
)1(
2
2
2
−
−
−
e
RI
β
=
β
2
865.0
2
RI