Bài tập về cực trị hàm số

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 2. Cực trị hàm số

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

A. LÝ THUYẾT.

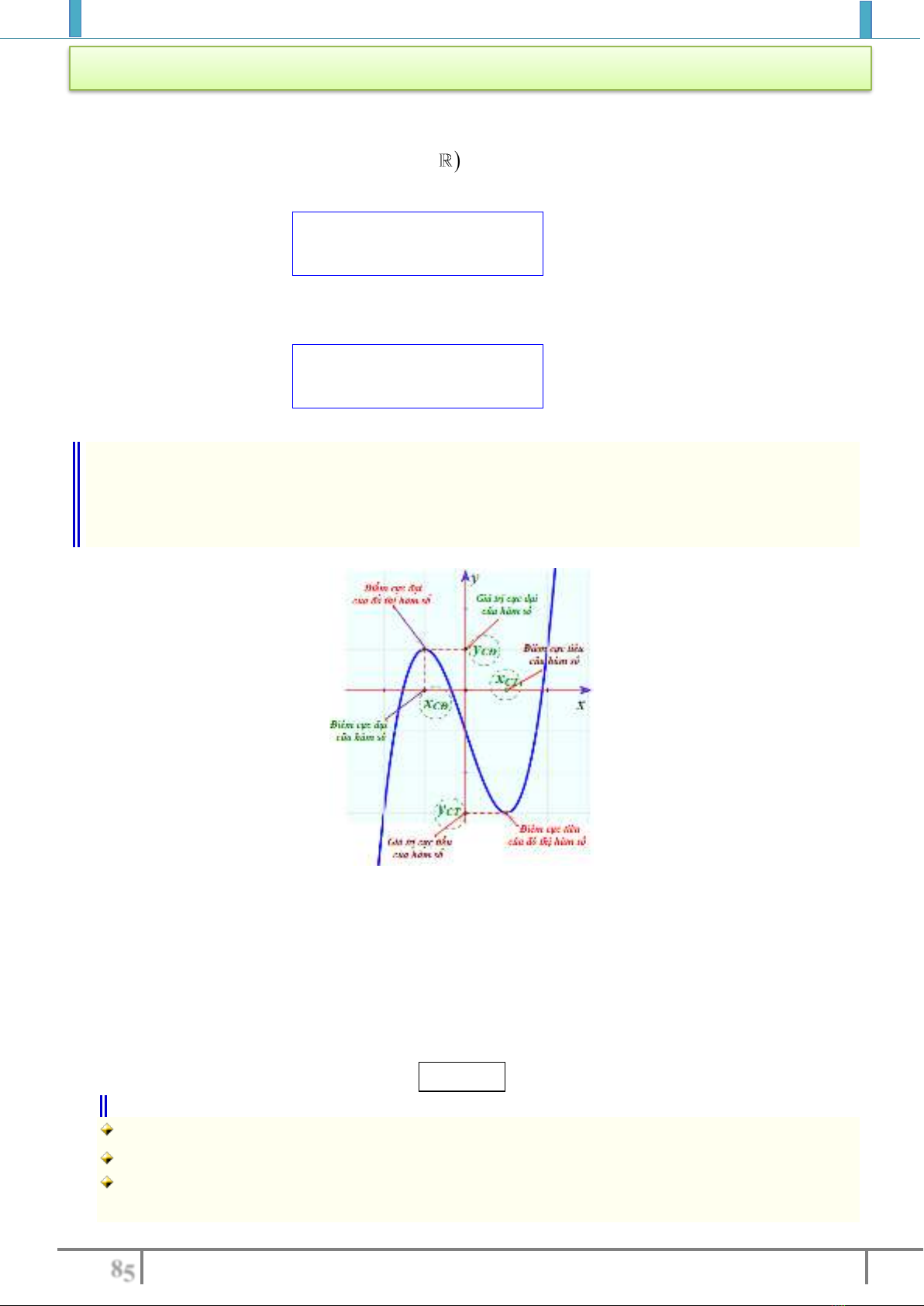
1. Khái niệm cực trị hàm số :

Giả sử hàm số xác định trên tập hợp

 

DD

và

0xD



được gọi là một điểm cực đại của hàm số

nếu tồn tại một khoảng

 

;ab

chứa điểm

sao cho:

 

   

;

( ) ( ) ; \

a b D

f x f x x a b x







  





Khi đó

 

được gọi là giá trị cực đại của hàm số



được gọi là một điểm cực tiểu của hàm số

nếu tồn tại một khoảng

 

;ab

chứa điểm

sao cho:

 

   

;

( ) ( ) ; \

a b D

f x f x x a b x







  





Khi đó

 

được gọi là giá trị cực tiểu của hàm số

Giá trị cực đại và giá trị cực tiểu được gọi chung là cực trị

Nếu

là một điểm cực trị của hàm số

thì người ta nói rằng hàm số

đạt cực trị tại điểm

 Điểm cực đại, cực tiểu gọi chung là điểm cực trị của hàm số



 

là giá trị cực trị (hay cực trị ) của hàm số.

Như vậy : Điểm cực trị phải là một điểm trong của tập hợp

``Chú ý.

 Giá trị cực đại (cực tiểu)

 

của hàm số

chưa hẳn đã là GTLN (GTNN) của hàm số

trên tập

xác định

mà

 

chỉ là GTLN (GTNN) của hàm số

trên khoảng

 

;a b D

và

 

;ab

chứa

điểm

0.x

 Nếu

 



không đổi dấu trên tập xác định

của hàm số

thì hàm số

không có cực trị .

2. Điều kiện cần để hàm số đạt cực trị:

2.1. Định lý 1: Giả sử hàm số

đạt cực trị tại điểm

Khi đó, nếu

có đạo hàm tại điểm

thì

 

'0fx

Chú ý :

Đạo hàm

có thể triệt tiêu tại điểm

nhưng hàm số

không đạt cực trị tại điểm

Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm.

Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng

hoặc tại

đó hàm số không có đạo hàm .

§BI 2. CỰC TRỊ CỦA HÀM SỐ

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 2. Cực trị hàm số

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

3. Điều kiện đủ để hàm số đạt cực trị:

Định lý 2: Giả sử hàm số

có đạo hàm cấp một trên khoảng

 

;ab

chứa điểm

 

'0fx

và

có đạo hàm cấp hai khác

tại điểm

Nếu

 

'' 0fx

thì hàm số

đạt cực đại tại điểm

Nếu

 

'' 0fx

thì hàm số

đạt cực tiểu tại điểm

Chú ý :

Nếu

là một điểm cực trị của hàm số

thì điểm

( ; ( ))x f x

được gọi là

điểm cực trị của đồ

thị

hàm số

Trong trường hợp

'( ) 0fx

không tồn tại hoặc

'( ) 0

''( ) 0









thì định lý 3

không dùng được.

B. PHƯƠNG PHÁP GIẢI TOÁN.

DẠNG 1. Tìm các điểm cực trị của hàm số.

1. Phương pháp.

① Bước 1. Tìm tập xác định của hàm số

② Bước 2. Tính đạo hàm

()



và tìm các điểm

sao cho

()



= 0 (nếu có) và tìm các điểm

0xD

mà tại đó hàm

liên tục nhưng đạo hàm

()



không tồn tại.

③ Bước 3. Vận dụng định lý 2 (lập bảng xét dấu

()



) hay định lý 3( tính

()



) để xác định

điểm cực trị của hàm số.

⋆ Chú ý:

Cho hàm số

()y f x

xác định trên

. Điểm

x x D

là điểm cực trị của hàm số khi và chỉ khi

hai điều kiện sau đây cùng thảo mãn:

 Tại

xx

đạo hàm triệt tiêu hoặc không tồn tại

 Đạo hàm đổi dấu khi

đi qua

2. Bài tập minh họa.

Bài tập 1. Tìm cực trị (nếu có) của các hàm số sau:

1).

21   y x x

2).

68   y x x x

Lời giải.

................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 2. Cực trị hàm số

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................................................

Nhận xét

. Trong bài toán này, vì

'(1) 0

''(1) 0









do đó

định lý 3

không khẳng định được điểm

2x

có

phải là điểm cực trị của hàm số hay không.

Bài tập 2. Tìm cực trị (nếu có) của các hàm số sau:

1).

361

    y x x x

2).

21   y x x x

Lời giải.

................................................................................................................................

Bài tập 3. Tìm cực trị (nếu có) của các hàm số sau:

1).





2).

   

yx x

Lời giải.

................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 2. Cực trị hàm số

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................................................

Bài tập 4. Tìm cực trị (nếu có) của hàm số :

3 2cos cos 2  y x x

Lời giải.

................................................................................................................................

Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 2. Cực trị hàm số

Lớp Toán Thầy-Diệp Tuân Tel: 0935.660.880

................................................................................................................................

Bài tập 5. Cho hàm số

 

sin , 0

0 , 0











fx x

. Chứng minh rằng

 

'0fx

nhưng hàm số

 

không đạt cực trị tại điểm

Lời giải.

................................................................................................................................

3. Câu hỏi trắc nghiệm

Mức độ 1. Nhận biết

Câu 1. Cho hàm số

33.y x x

Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng

 

;1 

và nghịch biến trên khoảng

 

1; 

B. Hàm số đồng biến trên khoảng

( ; ). 

C. Hàm số nghịch biến trên khoảng

 

;1 

và đồng biến trên khoảng

 

1; 

D. Hàm số nghịch biến trên khoảng

 

1;1

Lời giải

................................................................................................................................

Câu 2.(THPT Chuyên Bắc Ninh 2018) Phát biểu nào sau đây là sai?

A. Nếu

 

00fx



và

 

00fx

 

thì hàm số đạt cực tiểu tại

B. Nếu

 

00fx



và

 

00fx

 

thì hàm số đạt cực đại tại

C. Nếu

 



đổi dấu khi

qua điểm

và

 

liên tục tại

thì hàm số

 

y f x

đạt cực

trị tại điểm

D. Hàm số

 

y f x

đạt cực trị tại

khi và chỉ khi

là nghiệm của đạo hàm.

Lời giải

................................................................................................................................

Bài tập về cực trị hàm số

Tài liêu mới

Tài liệu Tổng hợp bài tập định lý Viète

Bài tập ôn luyện ngữ pháp tiếng Anh cơ bản

Bài tập vận dụng về từ vựng, ngữ pháp tiếng Anh

Bài tập So sánh hơn và nhất của tính từ

Tài liệu tham khảo Tiếng Anh lớp 8

Đề ôn tập Vật lí lớp 12

Tài liệu chuyên đề: Cực trị hàm số

Câu hỏi trắc nghiệm ôn tập môn Toán lớp 11

Tài liệu Tổng hợp lý thuyết Toán lớp 8

Tài liệu Lý thuyết và bài tập Tiếng Anh lớp 6

Tài liệu Bài tập cơ bản và nâng cao Đại số 7 (Dành cho giáo viên, phụ huynh)

Tài liệu bồi dưỡng học sinh giỏi môn Lịch sử lớp 9 (Sách Kết nối tri thức)

Tài liệu Hình học 9 - Chương 5: Đường tròn - Tự luận có lời giải (Sách Kết nối trí thức với cuộc sống)

Phiếu bài tập cuối tuần Tiếng Việt 1 - Tuần 1 đến tuần 5

Phiếu bài tập cuối tuần Tiếng Việt 1 - Tuần 2 - Đề 4

Giới thiệu

Về chúng tôi

Việc làm

Quảng cáo

Liên hệ

Chính sách

Thoả thuận sử dụng

Chính sách bảo mật

Chính sách hoàn tiền

DMCA

Hỗ trợ

Hướng dẫn sử dụng

Đăng ký tài khoản VIP

093 303 0098

support@tailieu.vn

Phương thức thanh toán

Theo dõi chúng tôi

Facebook

Youtube

TikTok

Bài tập về cực trị hàm số

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi